《理論》〈電気回路〉[R4上:問9]直列共振回路におけるコイルと抵抗の電圧の比に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

図のように，\( \ 5 \ \mathrm {\Omega } \ \)の抵抗，\( \ 200 \ \mathrm {mH} \ \)のインダクタンスをもつコイル，\( \ 20 \ \mathrm {\mu F} \ \)の静電容量をもつコンデンサを直列に接続した回路に周波数\( \ f \ \mathrm {[Hz]} \ \)の正弦波交流電圧\( \ E \ \mathrm {[V]} \ \)を加えた。周波数\( \ f \ \)を回路に流れる電流が最大となるように変化させたとき，コイルの両端の電圧の大きさは抵抗の両端の電圧の大きさの何倍か。最も近いものを次の(1)～(5)のうちから一つ選べ。

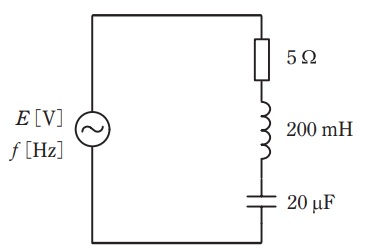
　(1)　\( \ 5 \ \)　　(2)　\( \ 10 \ \)　　(3)　\( \ 15 \ \)　　(4)　\( \ 20 \ \)　　(5)　\( \ 25 \ \)　　

【ワンポイント解説】

交流回路の共振条件から，各インピーダンスにかかる電圧を求める問題です。
まず問題文から共振回路であることを理解して，そこから回路計算を行う必要があります。
難易度は高そうですが，受験生のレベルが高いことを考えると順序立てて解けば解ける問題であることから，正答率は高いと予想されます。

1.直列回路の共振回路
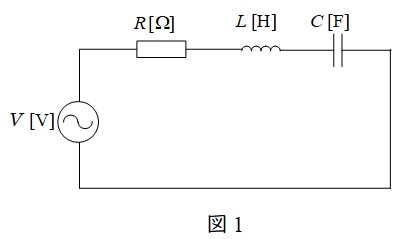
図1のような\( \ RLC \ \)直列回路があった場合の合成インピーダンス\( \ \dot Z \ \)は，角周波数を\( \ \omega \ \)とすると，
\[
\begin{eqnarray}
\dot Z&=&R+\mathrm {j}\omega L +\frac {1}{\mathrm {j}\omega C} \\[ 5pt ] &=&R+\mathrm {j}\left( \omega L -\frac {1}{\omega C}\right) \\[ 5pt ] \end{eqnarray}
\] となり，インピーダンスが最も小さくなるためには，上式の虚数部が零である必要があります。よって，共振角周波数\( \ \omega _{\mathrm {c}} \ \)は，
\[
\begin{eqnarray}
\omega_{\mathrm {c}} L -\frac {1}{\omega_{\mathrm {c}} C}&=&0 \\[ 5pt ] \omega_{\mathrm {c}} L &=&\frac {1}{\omega_{\mathrm {c}} C} \\[ 5pt ] \omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ] \omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。また，共振周波数を\( \ f_{\mathrm {c}} \ \)とすると，\( \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ \)より，
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。

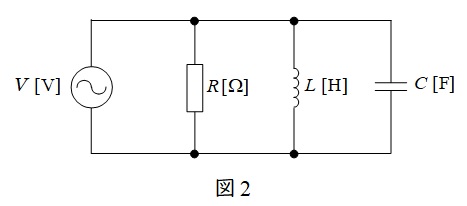
2.並列回路の共振回路
図2のような\( \ RLC \ \)並列回路があった場合の合成アドミタンス\( \ \dot Y \ \)は，角周波数を\( \ \omega \ \)とすると，
\[
\begin{eqnarray}
\dot Y&=&\frac {1}{R}+\mathrm {j}\omega C +\frac {1}{\mathrm {j}\omega L} \\[ 5pt ] &=&\frac {1}{R}+\mathrm {j}\left( \omega C -\frac {1}{\omega L}\right)
\end{eqnarray}
\] となり，アドミタンスが最も小さくなるためには，上式の虚数部が零である必要があります。よって，共振角周波数\( \ \omega _{\mathrm {c}} \ \)は，
\[
\begin{eqnarray}
\omega_{\mathrm {c}} C -\frac {1}{\omega_{\mathrm {c}} L}&=&0 \\[ 5pt ] \omega_{\mathrm {c}} C &=&\frac {1}{\omega_{\mathrm {c}} L} \\[ 5pt ] \omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ] \omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。また，共振周波数を\( \ f_{\mathrm {c}} \ \)とすると，\( \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ \)より，
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(4)
問題文において，「\( \ f \ \)を回路に流れる電流が最大となるように変化」となっていることから，周波数\( \ f \ \mathrm {[Hz]} \ \)は共振周波数であることがわかるので，ワンポイント解説「1.直列回路の共振回路」より，
\[
\begin{eqnarray}
f &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] &=& \frac {1}{2\pi \times \sqrt {200\times 10^{-3}\times 20\times 10^{-6}}} \\[ 5pt ] &=& \frac {1}{2\pi \times 2\times 10^{-3}} \\[ 5pt ] &=& \frac {250}{\pi }　\left( ≒ 79.6 \ \mathrm {[Hz]}\right) \\[ 5pt ] \end{eqnarray}
\] となり，このときのコイルとコンデンサのリアクタンス\( \ X_{\mathrm {L}} \ \mathrm {[\Omega ]} \ \)及び\( \ X_{\mathrm {C}} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
X_{\mathrm {L}} &=& 2\pi fL \\[ 5pt ] &=& 2\pi \times \frac {250}{\pi }\times 200\times 10^{-3} \\[ 5pt ] &=& 100 \ \mathrm {[\Omega ]} \\[ 5pt ] X_{\mathrm {C}} &=& \frac {1}{2\pi fC} \\[ 5pt ] &=& \frac {1}{\displaystyle 2\pi \times \frac {250}{\pi }\times 20\times 10^{-6}} \\[ 5pt ] &=& 100 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，回路を流れる電流\( \ I \ \mathrm {[A]} \ \)とすると，コイルの両端の電圧\( \ V_{\mathrm {L}} \ \mathrm {[V]} \ \)と抵抗の両端の電圧\( \ V_{\mathrm {R}} \ \mathrm {[V]} \ \)の比\( \ \displaystyle \frac {V_{\mathrm {L}}}{V_{\mathrm {R}}} \ \)は，
\[
\begin{eqnarray}
\frac {V_{\mathrm {L}}}{V_{\mathrm {R}}} &=& \frac {X_{\mathrm {L}}I}{RI} \\[ 5pt ] &=& \frac {X_{\mathrm {L}}}{R} \\[ 5pt ] &=& \frac {100}{5} \\[ 5pt ] &=& 20 \\[ 5pt ] \end{eqnarray}
\] と求められる。