《理論》〈電子理論〉[R4下:問12]真空中を動く電子の運動の向きと大きさの導出に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

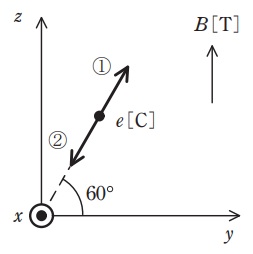
図のように，\( \ z \ \)軸の正の向きに磁束密度\( \ B=1.0\times 10^{-3} \ \mathrm {T} \ \)の平等磁界が存在する真空の空間において，電気量\( \ e=-4.0\times 10^{-6} \ \mathrm {C} \ \)の荷電粒子が\( \ yz \ \)平面上を\( \ y \ \)軸から\( \ 60° \ \)の角度で①又は②の向きに速さ\( \ v \ \mathrm {[m / s]} \ \)で発射された。この瞬間，荷電粒子に働くローレンツ力\( \ F \ \)の大きさは\( \ 1.0\times 10^{-8} \ \mathrm {N} \ \)，その向きは\( \ x \ \)軸の正の向きであった。荷電粒子の速さ\( \ v \ \)に最も近い値\( \ \mathrm {[m / s]} \ \)とその向きの組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

ただし，重力の影響は無視できるものとする。図中の\( \ \odot \ \)は，紙面に対して垂直かつ手前の向きを表す。

\[
\begin{array}{ccc}
& 速さ \ v \ & 向き \\
\hline
(1) & 　2.5　 & 　①　 \\
\hline
(2) & 　2.9　 & 　①　 \\
\hline
(3) & 　5.0　 & 　①　 \\
\hline
(4) & 　2.9　 & 　②　 \\
\hline
(5) & 　5.0　 & 　②　 \\
\hline
\end{array}
\]

【ワンポイント解説】

真空中の電子に加わる力から電子の運動方向及び大きさを求める問題です。
電子の運動の向きが電流の方向の逆の方向になることに注意して解くようにしましょう。
よくある電験の参考書の公式\( \ F=qvB\sin \theta \ \)をそのまま適用して間違えた受験生も多かったのではないかと予想されます。できるだけ丸暗記するのではなく原理を理解するようにしましょう。

1.フレミングの左手の法則
中指を電流の向き，人差し指を磁界の向きに合わせると，親指の方向に力が働くという法則で，頭文字を取って「電磁力」と覚えます。
磁束密度の大きさ\( \ B \ \)，電子の速度\( \ v \ \)，電子の電荷を\( \ e \ \)とすると，電子に加わるローレンツ力\( \ F \ \)は
\[
\begin{eqnarray}
F &=&evB \\[ 5pt ] \end{eqnarray}
\] となります。電子の場合，動く向きが電流の向きと逆になるので，中指の向きに注意するようにしましょう。

【解答】

解答：(5)
左手の親指を\( \ +x \ \)方向，人差し指を\( \ +z \ \)方向に向けると中指は\( \ +y \ \)方向を向く。
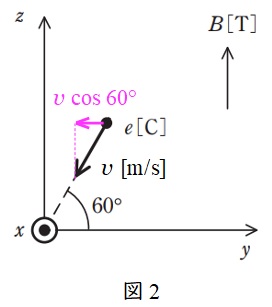
荷電粒子は電気量が負なので，運動方向は電流の向きと逆向きとなり，\( \ -y \ \)方向に動いていることになる。したがって，②が正しい。

また，図2に示すように荷電粒子の速度の\( \ -y \ \)方向は\( \ v\cos 60° \ \)であるため，ワンポイント解説「1.フレミングの左手の法則」のローレンツ力\( \ F \ \)を求める式より，
\[
\begin{eqnarray}
F &=&ev\cos 60°\times B \\[ 5pt ] v &=&\frac {F}{e\cos 60°\times B} \\[ 5pt ] &=&\frac {1.0\times 10^{-8}}{4.0\times 10^{-6}\times 0.5 \times 1.0\times 10^{-3}} \\[ 5pt ] &=&5.0 \ \mathrm {[m / s]} \\[ 5pt ] \end{eqnarray}
\] と求められる。