《理論》〈電磁気〉[R4下:問2]平行平板コンデンサ内の電気力線の特徴と導体球の電位に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図のように，平行板コンデンサの上下極板に挟まれた空間の中心に，電荷\( \ Q \ \mathrm {[C]} \ \)を帯びた導体球を保持し，上側極板の電位が\( \ E \ \mathrm {[V]} \ \)，下側極板の電位が\( \ -E \ \mathrm {[V]} \ \)となるように電圧源をつないだ。ただし，\( \ E＞0 \ \)とする。同図に，二つの極板と導体球の間の電気力線の様子を示している。

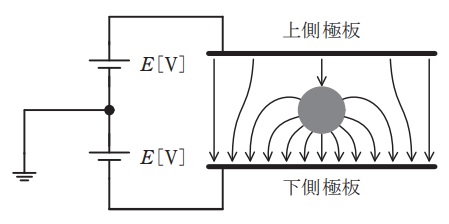
このとき，電荷\( \ Q \ \mathrm {[C]} \ \)の符号と導体球の電位\( \ U \ \mathrm {[V]} \ \)について，正しい記述のものを次の(1)～(5)のうちから一つ選べ。

(1)　\( \ Q＞0 \ \)であり，\( \ 0＜U＜E \ \)である。

(2)　\( \ Q＞0 \ \)であり，\( \ U=E \ \)である。

(3)　\( \ Q＞0 \ \)であり，\( \ 0＜E＜U \ \)である。

(4)　\( \ Q＜0 \ \)であり，\( \ U＜-E \ \)である。

(5)　\( \ Q＜0 \ \)であり，\( \ -E＜U＜0 \ \)である。

【ワンポイント解説】

平行平板コンデンサ内の電気力線の特徴に関する問題です。
電気力線の基本と電界の大きさと電位差が比例していることを理解していれば解ける問題となります。
問1の応用問題といった印象です。

1.電気力線の特徴
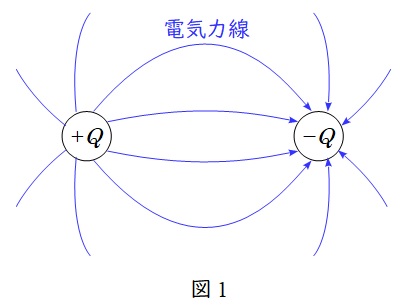
電気力線は正電荷から負電荷に向かう仮想の線で，以下のような特徴があります。言葉ではなく図で覚えておいて，内容を理解した方が良いと思います。
①電気力線の本数は電荷\( \ Q \ \mathrm {[C]} \ \)，誘電率\( \ \varepsilon \ \mathrm {[F/m]} \ \)を用いると，\( \ \displaystyle \frac {Q}{\varepsilon } \ \)本である。
②電気力線は正電荷から垂直に出て，負電荷に垂直に入る。
③電気力線同士は反発し合う。
④電気力線は枝分かれしたり，交差したりしない。
⑤電気力線の向きは電界の向きと一致し，電気力線の密度は電界の大きさに比例する。

2.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係
極板間の距離\( \ d \ \)の平行平板コンデンサに電圧\( \ V \ \)をかけると，極板間の電界\( \ E \ \)は，
\[
\begin{eqnarray}
E&=&\frac {V}{d} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(1)
問題図において，上側極板から導体球に入る電気力線より，導体球から下側極板に出ている電気力線の方が本数が多いため，\( \ Q＞0 \ \)である。

また，電気力線の本数は電界の大きさに比例し，電界の大きさが大きい方が電位差も大きくなるため，上側極板の電位\( \ E \ \mathrm {[V]} \ \)と導体球の電位\( \ U \ \mathrm {[V]} \ \)の電位差よりも，導体球の電位\( \ U \ \mathrm {[V]} \ \)と下側極板の電位\( \ -E \ \mathrm {[V]} \ \)の電位差の方が大きくなる。したがって，\( \ 0＜U＜E \ \)である。