《理論》〈電気回路〉[H29:問5]直流と４個の抵抗からなる回路に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

図のように直流電源と\( \ 4 \ \)個の抵抗からなる回路がある。この回路において\( \ 20 \ \Omega \ \)の抵抗に流れる電流\( \ I \ \)の値\( \ \left[ \mathrm {A}\right] \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　　

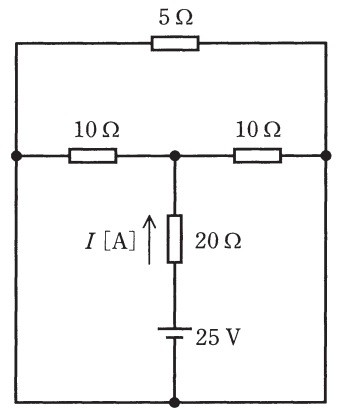
　(1)　\(0.5\)　　(2)　\(0.8\)　　(3)　\(1.0\)　　(4)　\(1.2\)　　(5)　\(1.5\)

【ワンポイント解説】

本問は回路の対称性に気が付けば，それほど難しい計算は必要ありません。分からない場合でも\( \ \Delta -\mathrm {Y} \ \)変換を用いれば，解くことが可能です。

1.直列と並列の合成抵抗
\( \ R_{1} \ \)と\( \ R_{2} \ \)の抵抗の合成抵抗\( \ R \ \)は以下の通りとなります。

①直列
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ] \end{eqnarray}
\]

②並列
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] すなわち，
\[
\begin{eqnarray}
R&=&\frac{R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\]

2.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y} -\Delta \ \)変換
①\( \ \Delta -\mathrm {Y} \ \)変換
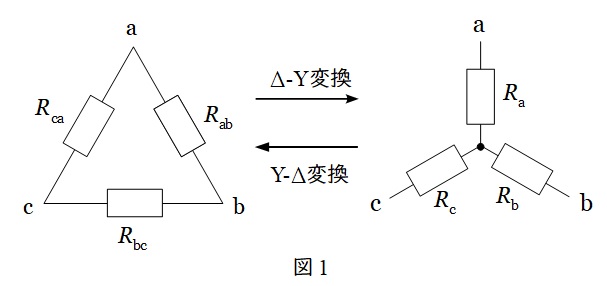
図1において，
\[
\begin{eqnarray}
R_{\mathrm {a}}&=&\frac {R_{\mathrm {ab}}R_{\mathrm {ca}}}{R_{\mathrm {ab}}+R_{\mathrm {bc}}+R_{\mathrm {ca}}} \\[ 5pt ] R_{\mathrm {b}}&=&\frac {R_{\mathrm {bc}}R_{\mathrm {ab}}}{R_{\mathrm {ab}}+R_{\mathrm {bc}}+R_{\mathrm {ca}}} \\[ 5pt ] R_{\mathrm {c}}&=&\frac {R_{\mathrm {ca}}R_{\mathrm {bc}}}{R_{\mathrm {ab}}+R_{\mathrm {bc}}+R_{\mathrm {ca}}} \\[ 5pt ] \end{eqnarray}
\] ②\( \ \mathrm {Y} -\Delta \ \)変換
図1において，
\[
\begin{eqnarray}
R_{\mathrm {ab}}&=&\frac {R_{\mathrm {a}}R_{\mathrm {b}}+R_{\mathrm {b}}R_{\mathrm {c}}+R_{\mathrm {c}}R_{\mathrm {a}}}{R_{\mathrm {c}}} \\[ 5pt ] R_{\mathrm {bc}}&=&\frac {R_{\mathrm {a}}R_{\mathrm {b}}+R_{\mathrm {b}}R_{\mathrm {c}}+R_{\mathrm {c}}R_{\mathrm {a}}}{R_{\mathrm {a}}} \\[ 5pt ] R_{\mathrm {ca}}&=&\frac {R_{\mathrm {a}}R_{\mathrm {b}}+R_{\mathrm {b}}R_{\mathrm {c}}+R_{\mathrm {c}}R_{\mathrm {a}}}{R_{\mathrm {b}}} \\[ 5pt ] \end{eqnarray}
\] ※\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y} -\Delta \ \)変換はなかなか覚えにくいですが，規則性を理解し，各変換の1個ずつの式を二次方程式の解の公式のように何度も唱え覚えるのが電験対策としては最も有効な手段と思います。

【関連する「電気の神髄」記事】

　　Y⇔Δ回路のインピーダンス変換式

【解答】

解答：(3)
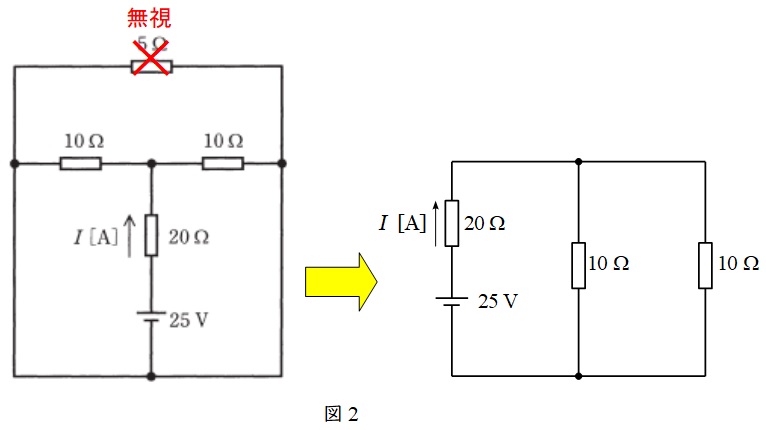
回路の対称性から，問題図の\( \ 5 \ \Omega \ \)の両端の電圧は等しい。従って\( \ 5 \ \Omega \ \)の抵抗には電流は流れないので無視できる。
これより，問題図の回路は図2のように書き換えられ，\( \ 10 \ \Omega \ \)の抵抗と\( \ 10 \ \Omega \ \)の抵抗の並列合成抵抗は，
\[
\begin{eqnarray}
\frac {10\times 10}{10+10}&=&5\left[ \Omega\right] \\[ 5pt ] \end{eqnarray}
\] となるため，回路全体の合成抵抗は，
\[
\begin{eqnarray}
20+5&=&25\left[ \Omega\right] \\[ 5pt ] \end{eqnarray}
\] となる。よって，\( \ 20 \ \Omega \ \)を流れる電流\( \ I \ \)は，
\[
\begin{eqnarray}
I&=&\frac {25}{25}=1.00\left[ \mathrm {A}\right] \\[ 5pt ] \end{eqnarray}
\] と求められる。

[別解]
ワンポイント解説「2.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y} -\Delta \ \)変換」の通り，\( \ 10 \ \Omega \ \)，\( \ 10 \ \Omega \ \)及び\( \ 5 \ \Omega \ \)で囲まれた抵抗の\( \ \Delta -\mathrm {Y} \ \)変換を行うと，図3のように求められる。
　　\( \ 10 \ \Omega \ \)と\( \ 10 \ \Omega \ \)の間の抵抗：\(\displaystyle \frac{10\times 10}{10+10+5}=4\left[ \Omega\right]\)

　　\( \ 10 \ \Omega \ \)と\( \ 5 \ \Omega \ \)の間の抵抗：\(\displaystyle \frac{10\times 5}{10+10+5}=2\left[ \Omega\right]\)

　

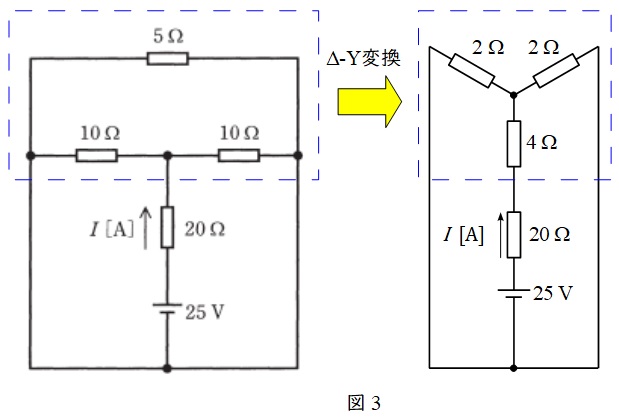
図3の\( \ 2 \ \Omega \ \)の抵抗と\( \ 2 \ \Omega \ \)の抵抗の並列合成抵抗は，
\[
\begin{eqnarray}
\frac {2\times 2}{2+2}&=&1\left[ \Omega\right] \\[ 5pt ] \end{eqnarray}
\] となり，回路全体の合成抵抗は，
\[
\begin{eqnarray}
20+4+1&=&25\left[ \Omega\right] \\[ 5pt ] \end{eqnarray}
\] となる。よって，\( \ 20 \ \Omega \ \)を流れる電流\( \ I \ \)は，
\[
\begin{eqnarray}
I&=&\frac {25}{25} \\[ 5pt ] &=&1.00\left[ \mathrm {A}\right] \\[ 5pt ] \end{eqnarray}
\] と求められる。