《理論》〈電気回路〉[R05上:問6]電圧源と電流源を含む回路の抵抗に流れる電流に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

図のような直流回路において，\( \ 3 \ \mathrm {\Omega } \ \)の抵抗を流れる電流の値\( \ \mathrm {[A]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

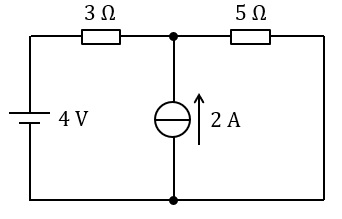
　(1)　\( \ 0.35 \ \)　　(2)　\( \ 0.45 \ \)　　(3)　\( \ 0.55 \ \)　　(4)　\( \ 0.65 \ \)　　(5)　\( \ 0.75 \ \)

【ワンポイント解説】

電圧源と電流源を含む回路の抵抗に流れる電流を求める問題です。
キルヒホッフの法則もしくは重ね合わせの理で解くことできそうです。解答ではキルヒホッフの法則を用いて，別解として重ね合わせの理を用いて解説します。
やや古い過去問ですが平成9年問5の再出題となります。

1.重ね合わせの理
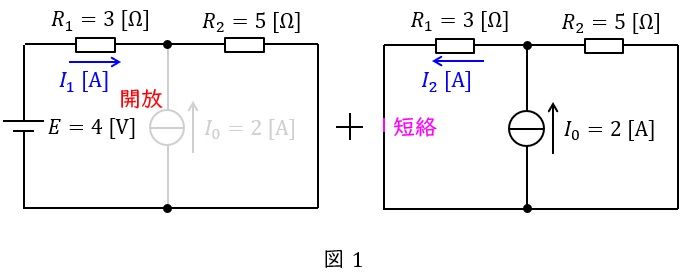
複数の電源で構成された回路は，電源毎に計算した電流を重ね合わせて求めることができます。この時，電圧源は短絡，電流源は開放します。本問において回路は図1のように分解できます。

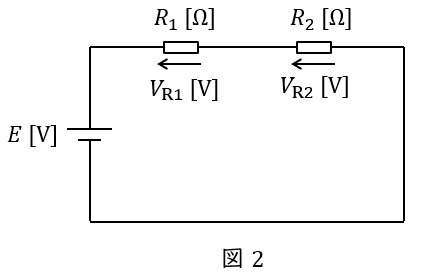
2.分圧・分流の法則
①分圧の法則
図2に示した直列回路において，各抵抗にかかる電圧は以下の通りとなります。
\[
\begin{eqnarray}
V_{\mathrm {R1}}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ] V_{\mathrm {R2}}&=&\frac {R_{2}}{R_{1}+R_{2}}E \\[ 5pt ] \end{eqnarray}
\]

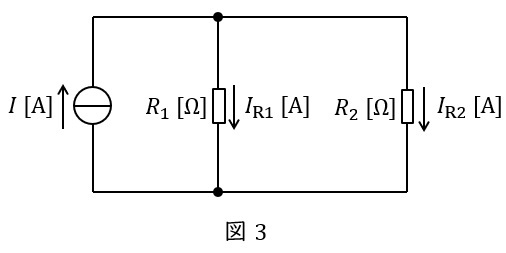
②分流の法則
図3に示した並列回路において，各抵抗に流れる電流は以下の通りとなります。分子の抵抗が分圧の法則と逆となることに注意して下さい。
\[
\begin{eqnarray}
I_{\mathrm {R1}}&=&\frac {\color{red}{R_{2}}}{R_{1}+R_{2}}I \\[ 5pt ] I_{\mathrm {R2}}&=&\frac {\color{red}{R_{1}}}{R_{1}+R_{2}}I \\[ 5pt ] \end{eqnarray}
\]

【関連する「電気の神髄」記事】

　　重ね合わせの理の証明

【解答】

解答：(5)
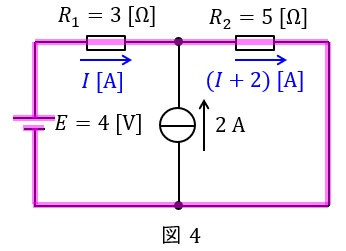
\( \ R_{1}=3 \ \mathrm {[\Omega ]} \ \)に流れる電流を\( \ I \ \mathrm {[A]} \ \)とすると，キルヒホッフの法則の電流則より，\( \ R_{2}=5 \ \mathrm {[\Omega ]} \ \)に流れる電流は\( \ \left( I+2\right) \ \mathrm {[A]} \ \)となる。したがって，図4に示す閉回路にキルヒホッフの法則の電圧則を適用すると，
\[
\begin{eqnarray}
E&=&R_{1}I+R_{2}\left( I+2\right) \\[ 5pt ] 4&=&3I+5\left( I+2\right) \\[ 5pt ] 4&=&3I+5I+10 \\[ 5pt ] 8I&=&-6 \\[ 5pt ] I&=&-0.75 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，大きさは\( \ 0.75 \ \mathrm {[A]} \ \)（左向き）と求められる。

【別解】
重ね合わせの理を適用して，各電源毎に分けると図1のようになる。図1左の回路について，\( \ R_{1}=3 \ \mathrm {[\Omega ]} \ \)に流れる電流\( \ I_{1} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{1}&=&\frac {E}{R_{1}+R_{2}} \\[ 5pt ] &=&\frac {4}{3+5} \\[ 5pt ] &=&0.5 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，図1右の回路について，\( \ R_{1}=3 \ \mathrm {[\Omega ]} \ \)に流れる電流\( \ I_{2} \ \mathrm {[A]} \ \)は，ワンポイント解説「2.分圧・分流の法則」の通り分流の法則を適用すると，
\[
\begin{eqnarray}
I_{2}&=&\frac {R_{2}}{R_{1}+R_{2}}I_{0} \\[ 5pt ] &=&\frac {5}{3+5}\times 2 \\[ 5pt ] &=&1.25 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，ワンポイント解説「1.重ね合わせの理」より，求める電流\( \ I \ \mathrm {[A]} \ \)は，電流の向きに注意すると，
\[
\begin{eqnarray}
I&=&I_{2}-I_{1} \\[ 5pt ] &=&1.25-0.5 \\[ 5pt ] &=&0.75 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。