《理論》〈電子理論〉[R06上:問12]平等電界中の電子の運動に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

真空中に置かれた平行電極板間に，直流電圧\( \ V \ \mathrm {[V]} \ \)を加えて平等電界\( \ E \ \mathrm {[V / m]} \ \)を作り，この陰極板に電子を置いた場合，初速零で出発した電子が陽極板に到達したときの速さは，\( \ v \ \mathrm {[m / s]} \ \)となった。このときの電子の運動エネルギーは，電子が陽極板に到達するまでに得るエネルギーに等しいと考えられ，次の式が成立する。
\[
\begin{eqnarray}
\frac {1}{2}mv^{2} &=& \ \fbox {　 （ア） 　} \ \\[ 5pt ] \end{eqnarray}
\] ただし，電子の電気素量を\( \ e \ \mathrm {[C]} \ \)，電子の質量を\( \ m \ \mathrm {[kg]} \ \)とする。

したがって，この式から電子の速さ\( \ v \ \mathrm {[m / s]} \ \)は，\( \ \fbox {　 （イ） 　} \ \)で表される。

上記の記述中の空白箇所(ア)及び(イ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{ccc}
& （ア） & （イ） \\
\hline
(1) & 　eV　 & 　\displaystyle \sqrt {\frac {4eV}{m}}　 \\
\hline
(2) & 　eV　 & 　\displaystyle \sqrt {\frac {2eV}{m}}　 \\
\hline
(3) & 　2eV　 & 　\displaystyle \sqrt {\frac {4eV}{m}}　 \\
\hline
(4) & 　eE　 & 　\displaystyle \sqrt {\frac {2eE}{m}}　 \\
\hline
(5) & 　eE　 & 　\displaystyle \sqrt {\frac {4eE}{m}}　 \\
\hline
\end{array}
\]

【ワンポイント解説】

平等電界中の電子の持つエネルギーが変わらないエネルギー保存則を利用して，電子の速さを求める問題です。
計算量も比較的少なくパターンも決まっている問題なので，必ず理解しておきましょう。
本問は平成9年問9からの再出題となります。

1.一様電界中において電子に働く力と電子の持つエネルギー
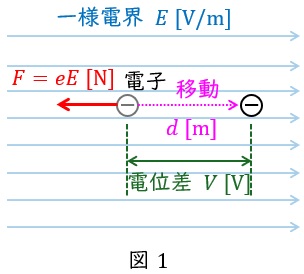
図1に示すように，一様な電界\( \ E \ \mathrm {[V／m]} \ \)中に電子\( \ -e \ \mathrm {[C]} \ \)があるとき，この電子に働く力の大きさ\( \ F \ \mathrm {[N]} \ \)は，
\[
\begin{eqnarray}
F &=&eE \\[ 5pt ] \end{eqnarray}
\] で向きは電界の向きと逆向きとなります。この電子を力の向きに逆らって\( \ d \ \mathrm {[m]} \ \)移動させるのに必要な仕事\( \ W \ \mathrm {[J]} \ \)は，
\[
\begin{eqnarray}
W &=&Fd \\[ 5pt ] &=&eEd \\[ 5pt ] \end{eqnarray}
\] であり，電界\( \ E \ \mathrm {[V／m]} \ \)と電位差\( \ V \ \mathrm {[V]} \ \)の関係\( \ V=Ed \ \)より，
\[
\begin{eqnarray}
W &=&eV \\[ 5pt ] \end{eqnarray}
\] となります。これは，外力により電子に蓄えられた位置エネルギーと言えます。

2.物体の運動エネルギー（力学）
質量\( \ m \ \mathrm {[kg]} \ \)の物体が，速度\( \ v \ \mathrm {[m／s]} \ \)で運動しているときの運動エネルギー\( \ K \ \mathrm {[J]} \ \)は，
\[
\begin{eqnarray}
K &=&\frac {1}{2}mv^{2} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(2)
(ア)
ワンポイント解説「1.一様電界中において電子に働く力と電子の持つエネルギー」の通り，電子の持つエネルギー（陽極板に到達するまでに得るエネルギー）は\( \ eV \ \mathrm {[J]} \ \)となります。

(イ)
（ア）の解答式より，
\[
\begin{eqnarray}
\frac {1}{2}mv^{2}&=&eV \\[ 5pt ] v^{2}&=&\frac {2eV}{m} \\[ 5pt ] v&=&\sqrt {\frac {2eV}{m}} \\[ 5pt ] \end{eqnarray}
\] と求められます。