《理論》〈電子理論〉[R06下:問12]マグネトロン内の電子の軌跡に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，電子レンジに内蔵されてマイクロ波を発生する，マグネトロン内の電子の軌跡を簡略化して説明した記述である。

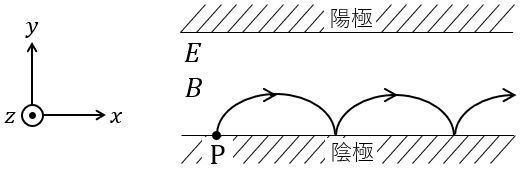
図に示すように，真空中の平行平板電極間に直流電圧を加えて平等電界\( \ E \ \mathrm {[V/m]} \ \)を作り，平等電界と直交する方向に磁束密度\( \ B \ \mathrm {[T]} \ \)の平等磁界を加えた。図中の\( \ \large{ \odot } \ \)は\( \ z \ \)軸の正の向きで，紙面に垂直かつ手前の向きを表す。

陰極上の点\( \ \mathrm {P} \ \)に初速零で電荷\( \ -e \ \mathrm {[C]} \ \)の電子を置いて静かに離すと，\( \ y \ \)軸の\( \ \fbox {　（ア）　} \ \)の向きの電界により電子は陽極に向かって動き始める。同時に電子は磁束密度に\( \ \fbox {　（イ）　} \ \)した大きさの\( \ \fbox {　（ウ）　} \ \)力を受ける。磁界は\( \ z \ \)軸の\( \ \fbox {　（エ）　} \ \)の向きのため，電子は電界と磁界の作用で\( \ x \ \)軸の正の向きに移動する。このとき磁束密度が一定値以上では電子は陽極に到達せずに，図のように\( \ \fbox {　（オ）　} \ \)といわれる軌跡を描く。ただし，電子は紙面と平行な平面上を移動し，重力の影響は無視できるものとする。

上記の記述中の空白箇所(ア)～(オ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{cccccc}
& （ア） & （イ） & （ウ） & （エ） & （オ） \\
\hline
(1) & 　正　 & 　比例　 & 　ローレンツ　 & 　正　 & 　サイクロイド　 \\
\hline
(2) & 　正　 & 　反比例　 & 　アンペール　 & 　正　 & 　ヒステリシス　 \\
\hline
(3) & 　負　 & 　比例　 & 　アンペール　 & 　負　 & 　リサジュー　 \\
\hline
(4) & 　負　 & 　比例　 & 　ローレンツ　 & 　負　 & 　サイクロイド　 \\
\hline
(5) & 　負　 & 　反比例　 & 　ローレンツ　 & 　負　 & 　リサジュー　 \\
\hline
\end{array}
\]

【ワンポイント解説】

マグネトロン内の電子の運動に関する問題です。
内容は難解そうに見えますが、内容は電磁気で学習する電界と磁界により発生する力を理解しているかどうかが問われています。
試験本番では知らない用語が出てくると焦ってしまうかもしれませんが，落ち着いて問題文を読み解いていくようにして下さい。

1.電荷に働く力の大きさ
一様な電界\( \ E \ \mathrm {[V / m]} \ \)が電荷\( \ q \ \mathrm {[C]} \ \)に加わっているとき，この電荷\( \ q \ \mathrm {[C]} \ \)に働く力の大きさ\( \ F \ \mathrm {[N]} \ \)は，
\[
\begin{eqnarray}
F &=&qE \\[ 5pt ] \end{eqnarray}
\] となります。電子の場合は，電荷がマイナスなので，電界と逆方向の力が加わります。

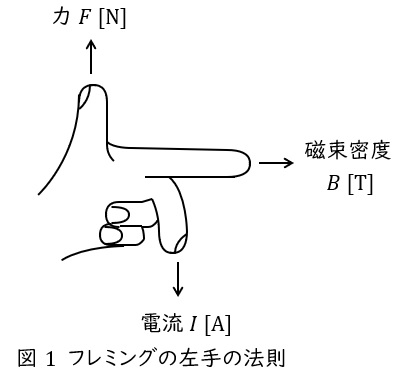
2.フレミングの左手の法則
中指を電流の向き，人差し指を磁界の向きに合わせると，親指の方向に力が働くという法則で，頭文字を取って「電磁力」と覚えます。
磁束密度の大きさ\( \ B \ \mathrm {[T]} \ \)，電子の速度\( \ v \ \mathrm {[m/s]} \ \)，電子の電荷を\( \ e \ \mathrm {[C]} \ \)とすると，電子にかかるローレンツ力\( \ F \ \mathrm {[N]} \ \)は，
\[
\begin{eqnarray}
F &=&evB \\[ 5pt ] \end{eqnarray}
\] となります。電子の場合，動く向きが電流の向きと逆になるので，中指の向きに注意するようにしましょう。

【解答】

解答：(4)
(ア)
ワンポイント解説「1.電荷に働く力の大きさ」の通り，電界は陽極から陰極に向かうので，\( \ y \ \)軸の負の向きとなります。

(イ)
ワンポイント解説「2.フレミングの左手の法則」の通り，電子には磁束密度に比例した力が加わります。

(ウ)
ワンポイント解説「2.フレミングの左手の法則」の通り，磁束密度により電子に加わる力をローレンツ力といいます。

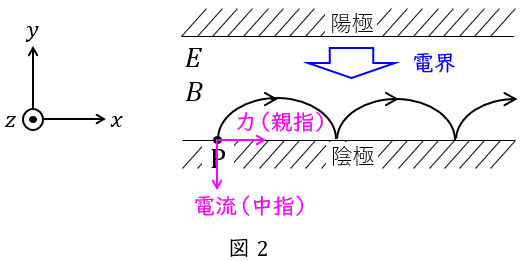
(エ)
図2に示す通り，点\( \ \mathrm {P} \ \)においては，電界により電子が\( \ y \ \)軸の正方向に動き始め，磁界により\( \ x \ \)軸の正方向に力が加わっているので，ワンポイント解説「2.フレミングの左手の法則」の通り，フレミングの法則を適用すると，磁界（人差し指）の向きは\( \ z \ \)軸の負の向きとなります。