《理論》〈電子理論〉[R06下:問18]演算増幅器の特徴と回路演算に関する論説・計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

演算増幅器（オペアンプ）について，次の(a)及び(b)の問に答えよ。

(a)　演算増幅器の特徴に関する記述として，誤っているものを次の(1)～(5)のうちから一つ選べ。

　(1)　アナログ\( \ \mathrm {IC} \ \)の一種である。

　(2)　入力インピーダンスが小さくて出力インピーダンスが大きい。

　(3)　反転並びに非反転の二つの入力端子と一つの出力端子がある。

　(4)　入力端子間の電圧のみを増幅して出力する。

　(5)　増幅度が非常に大きい。

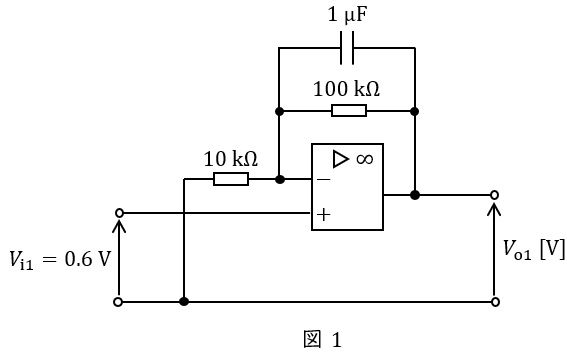
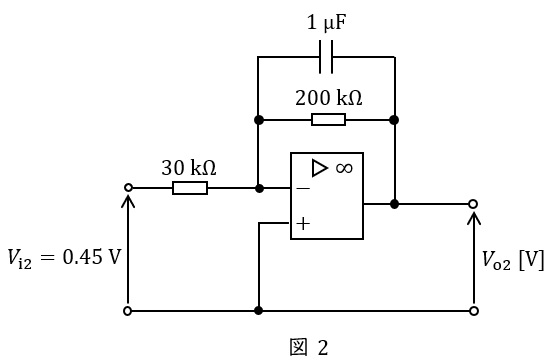
(b)　図1及び図2のような直流増幅回路がある。それぞれの出力電圧\( \ V_{\mathrm {o1}} \ \)，\( \ V_{\mathrm {o2}} \ \)の値\( \ \mathrm {[V]} \ \)の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

ただし，演算増幅器は理想的なものとし，\( \ V_{\mathrm {i1}}=0.6 \ \mathrm {V} \ \)及び\( \ V_{\mathrm {i2}}=0.45 \ \mathrm {V} \ \)は直流の入力電圧である。

\[
\begin{array}{ccc}
& 　V_{\mathrm {o1}}　 & 　V_{\mathrm {o2}}　 \\
\hline
(1) & 　6.6　 & 　-3.0　 \\
\hline
(2) & 　6.6　 & 　3.0　 \\
\hline
(3) & 　-6.6　 & 　3.0　 \\
\hline
(4) & 　-4.5　 & 　9.0　 \\
\hline
(5) & 　4.5　 & 　-9.0　 \\
\hline
\end{array}
\]

【ワンポイント解説】

演算増幅器に関する問題です。
基本的には選択問題で出題される内容ですが，必須問題で出題される可能性もあるので，演算増幅器の内容は理解しておきましょう。
演算増幅器は慣れてしまえば得点源となり得る問題も多いです。
本問は平成22年問18と酷似した類題となります。

1.理想的な演算増幅器の特徴
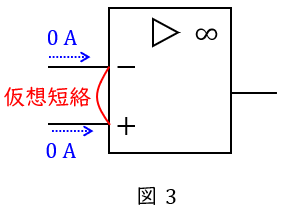
　１．電圧増幅率が無限大である。したがって，無限大でない有限数が出力される時，入力端子間の電圧は\( \ 0 \ \mathrm {V} \ \)(バーチャルショート)となる。
　２．入力インピーダンスが無限大である。したがって入力端子に電流は流れない。
　３．出力インピーダンスがゼロである。

【解答】

(a)解答：(2)
(1)：正しい
問題文の通り，演算増幅器はアナログ\( \ \mathrm {IC} \ \)の一種となります。

(2)：誤り
ワンポイント解説「1.理想的な演算増幅器の特徴」の通り，演算増幅器は入力インピーダンスが非常に大きく，出力インピーダンスが非常に小さい機器です。

(3)：正しい
ワンポイント解説「1.理想的な演算増幅器の特徴」の通り，反転増幅\( \ \left( -\right) \ \)と非反転増幅\( \ \left( +\right) \ \)の二つの入力端子と一つの出力端子があります。

(4)：正しい
問題文の通り，演算増幅器は入力端子間の電圧のみを増幅して出力する一種の差動増幅器と言えます。

(5)：正しい
ワンポイント解説「1.理想的な演算増幅器の特徴」の通り，演算増幅器の増幅度は非常に大きいです。

(b)解答：(1)
定常状態において，コンデンサは開放と考えれば良いので無視して考える。

図1において演算増幅器の非反転入力\( \ \left( +\right) \ \)の電位\( \ V_{\mathrm {+}} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {+}}&=&V_{\mathrm {i1}} \\[ 5pt ] &=&0.6 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] であり，ワンポイント解説「1.理想的な演算増幅器の特徴」の通り，入力端子間の電圧は\( \ 0 \ \mathrm {V} \ \)なので，反転入力\( \ \left( -\right) \ \)の電位\( \ V_{\mathrm {-}} \ \mathrm {[V]} \ \)も，
\[
\begin{eqnarray}
V_{\mathrm {-}}&=&V_{\mathrm {+}} \\[ 5pt ] &=&0.6 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] である。したがって，\( \ R_{11}=10 \ \mathrm {[k\Omega ]} \ \)の抵抗に流れる電流\( \ I_{1} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{1}&=&\frac {V_{\mathrm {-}}}{R_{11}} \\[ 5pt ] &=&\frac {0.6}{10\times 10^{3}} \\[ 5pt ] &=&0.06\times 10^{-3} \\[ 5pt ] &=&6.0\times 10^{-5} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，入力端子に電流が流れないので，\( \ R_{12}=100 \ \mathrm {[k\Omega ]} \ \)の抵抗に流れる電流も\( \ I_{1}=6.0\times 10^{-5} \ \mathrm {[A]} \ \)となる。よって，出力電圧\( \ V_{\mathrm {o1}} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {o1}}&=&V_{\mathrm {-}}+R_{12}I_{1} \\[ 5pt ] &=&0.6+\left( 100\times 10^{3}\right) \times \left( 6.0\times 10^{-5}\right) \\[ 5pt ] &=&6.6 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

次に，図2において，演算増幅器の非反転入力\( \ \left( +\right) \ \)の電位\( \ V_{\mathrm {+}} \ \mathrm {[V]} \ \)は\( \ 0 \ \mathrm {V} \ \)であり，ワンポイント解説「1.理想的な演算増幅器の特徴」の通り，入力端子間の電圧は\( \ 0 \ \mathrm {V} \ \)なので，反転入力\( \ \left( -\right) \ \)の電位\( \ V_{\mathrm {-}} \ \mathrm {[V]} \ \)も\( \ 0 \ \mathrm {V} \ \)である。
したがって，\( \ R_{21}=30 \ \mathrm {[k\Omega ]} \ \)の抵抗に流れる電流\( \ I_{2} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{2}&=&\frac {V_{\mathrm {i2}}-V_{\mathrm {-}}}{R_{21}} \\[ 5pt ] &=&\frac {0.45-0}{30\times 10^{3}} \\[ 5pt ] &=&0.015\times 10^{-3} \\[ 5pt ] &=&1.5\times 10^{-5} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，入力端子に電流が流れないので，\( \ R_{22}=200 \ \mathrm {[k\Omega ]} \ \)の抵抗に流れる電流も\( \ I_{2}=1.5\times 10^{-5} \ \mathrm {[A]} \ \)となる。よって，出力電圧\( \ V_{\mathrm {o2}} \ \mathrm {[V]} \ \)は，電流の向きに注意すると，
\[
\begin{eqnarray}
V_{\mathrm {o2}}&=&V_{\mathrm {-}}-R_{22}I_{2} \\[ 5pt ] &=&0-\left( 200\times 10^{3}\right) \times \left( 1.5\times 10^{-5}\right) \\[ 5pt ] &=&-3.0 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。