《理論》〈電気回路〉[R06下:問8]位相と波高値が異なる電源の合成電圧に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

図のように，二つの正弦波交流電圧源\( \ e_{1} \ \mathrm {[V]} \ \)，\( \ e_{2} \ \mathrm {[V]} \ \)が直列に接続されている回路において，合成電圧\( \ v \ \mathrm {[V]} \ \)の最大値は\( \ e_{1} \ \)の最大値の\( \ \fbox {　 （ア） 　} \ \)倍となり，その位相は\( \ e_{1} \ \)を基準として\( \ \fbox {　 （イ） 　} \ \mathrm {[rad]} \ \)の\( \ \fbox {　 （ウ） 　} \ \)となる。

上記の記述中の空白箇所(ア)～(ウ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
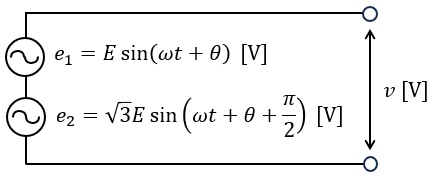
\begin{array}{cccc}
& （ア） & （イ） & （ウ） \\
\hline
(1) & 　\displaystyle \frac {1}{2}　 & 　\displaystyle \frac {\pi }{3}　 & 　進み　 \\
\hline
(2) & 　1+\sqrt {3}　 & 　\displaystyle \frac {\pi }{6}　 & 　遅れ　 \\
\hline
(3) & 　2　 & 　\displaystyle \frac {\pi }{3}　 & 　進み　 \\
\hline
(4) & 　\sqrt {3}　 & 　\displaystyle \frac {\pi }{6}　 & 　遅れ　 \\
\hline
(5) & 　2　 & 　\displaystyle \frac {2\pi }{3}　 & 　進み　 \\
\hline
\end{array}
\]

【ワンポイント解説】

位相と波高値が異なる交流電源の直列接続に関する問題です。
ベクトル図を描ければ難解ではありませんが，解法に気付けるかどうかが最大のポイントとなります。

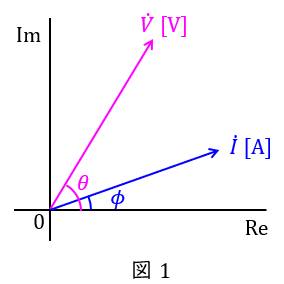
1.電圧・電流の瞬時値からの電力の導出
電圧及び電流の実効値が\( \ V \ \mathrm {[V]} \ \)及び\( \ I \ \mathrm {[A]} \ \)，角周波数が\( \ \omega \ \mathrm {[rad / s]} \ \)，電圧及び電流の初期位相が\( \ \theta \ \mathrm {[rad]} \ \)及び\( \ \phi \ \mathrm {[rad]} \ \)の正弦波交流があるとき，それぞれの瞬時値は，
\[
\begin{eqnarray}
v &=& \sqrt {2}V \sin \left( \omega t +\theta \right) \\[ 5pt ] i &=& \sqrt {2}I \sin \left( \omega t +\phi \right) \\[ 5pt ] \end{eqnarray}
\] となり，極座標平面では図1のように表されます。

【解答】

解答：(3)
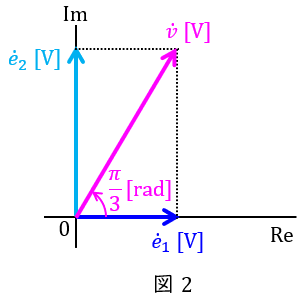
\( \ e_{1} \ \mathrm {[V]} \ \)を基準として，\( \ e_{2} \ \mathrm {[V]} \ \)及び合成電圧\( \ v \ \mathrm {[V]} \ \)を描く図2のようになる。

(ア)
図2より，\( \ \dot {e}_{2} \ \mathrm {[V]} \ \)の大きさは\( \ \dot {e}_{1} \ \mathrm {[V]} \ \)の\( \ \sqrt {3} \ \)倍なので，\( \ \dot v \ \mathrm {[V]} \ \)の大きさは\( \ 2 \ \)倍となり，波高値（最大値）も\( \ 2 \ \)倍となる。

(イ)
図2より，\( \ \dot v \ \mathrm {[V]} \ \)の位相は\( \ \displaystyle \frac {\pi }{3} \ \mathrm {[rad]} \ \)となる。

(ウ)
図2より，\( \ \dot v \ \mathrm {[V]} \ \)は\( \ \dot {e}_{1} \ \mathrm {[V]} \ \)より進み位相となる。