《理論》〈電磁気〉[R07上:問1]２つのコンデンサに蓄えられる静電エネルギーに関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

電圧\( \ V \ \mathrm {[V]} \ \)に充電された静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサと全く充電されていない静電容量\( \ 2C \ \mathrm {[F]} \ \)のコンデンサとがある。これら二つのコンデンサを並列に接続したとき，これらのコンデンサに蓄えられる全静電エネルギ一\( \ \mathrm {[J]} \ \)の値として，正しいものは次のうちどれか。

　(1)　\( \ \displaystyle \frac {1}{9}CV^{2} \ \)　　(2)　\( \ \displaystyle \frac {1}{6}CV^{2} \ \)　　(3)　\( \ \displaystyle \frac {2}{9}CV^{2} \ \)

　(4)　\( \ \displaystyle \frac {1}{3}CV^{2} \ \)　　(5)　\( \ \displaystyle \frac {3}{8}CV^{2} \ \)

【ワンポイント解説】

２つのコンデンサを並列接続したときに蓄えられる静電エネルギーに関する問題です。
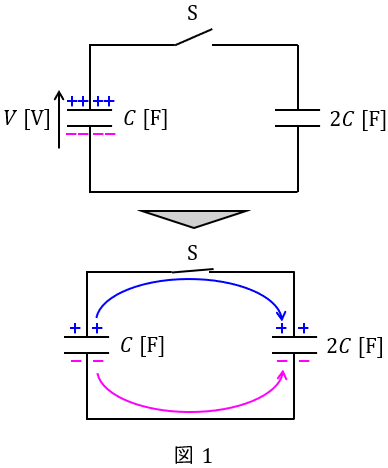
図が与えられていないので，しっかりと図1のような図を描いて整理していくことが重要です。また，本問に使用される公式はいずれも重要公式なので，しっかりと理解しておくようにしましょう。
本問は平成10年問6とほぼ同じ問題となります。

1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係
平行平板コンデンサにおいて，蓄えられる電荷\( \ Q \ \mathrm {[C]} \ \)と静電容量\( \ C \ \mathrm {[F]} \ \)及び電圧\( \ V \ \mathrm {[V]} \ \)には，
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ] \end{eqnarray}
\] の関係があります。

2.コンデンサの合成静電容量
コンデンサ容量が\( \ C_{1} \ \mathrm {[F]} \ \)と\( \ C_{2} \ \mathrm {[F]} \ \)のコンデンサがある場合，直並列の合成静電容量\( \ C \ \mathrm {[F]} \ \)は下記の通りとなります。抵抗の場合と直並列が逆になることを知っておきましょう。
①並列回路の合成静電容量
\[
\begin{eqnarray}
C&=&C_{1}+C_{2} \\[ 5pt ] \end{eqnarray}
\] ②直列回路の合成静電容量
\[
\begin{eqnarray}
\frac {1}{C}&=&\frac {1}{C_{1}}+\frac {1}{C_{2}} \\[ 5pt ] \end{eqnarray}
\] 整理すると，
\[
\begin{eqnarray}
C&=&\frac {C_{1}C_{2}}{C_{1}+C_{2}} \\[ 5pt ] \end{eqnarray}
\]

3.コンデンサの静電エネルギー\( \ W \ \)
コンデンサの静電エネルギー\( \ W \ \mathrm {[J]} \ \)は，コンデンサの静電容量\( \ C \ \mathrm {[F]} \ \)及びコンデンサに加わる電圧\( \ V \ \mathrm {[V]} \ \)とすると，
\[
\begin{eqnarray}
W &=&\frac {1}{2}CV^{2} \\[ 5pt ] \end{eqnarray}
\] であり，\( \ Q=CV \ \)の関係から，
\[
\begin{eqnarray}
W&=&\frac {1}{2}QV \\[ 5pt ] &=&\frac {Q^{2}}{2C} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(2)
本問は電荷を蓄えた\( \ C \ \mathrm {[F]} \ \)のコンデンサと蓄えていない\( \ 2C \ \mathrm {[F]} \ \)のコンデンサを並列に接続したとなっているので，図1に示すスイッチ\( \ \mathrm {S} \ \)を組み合わせた回路と等価であると考えられる。

図1において，スイッチ\( \ \mathrm {S} \ \)投入前に\( \ C \ \mathrm {[F]} \ \)のコンデンサに蓄えられる電荷\( \ Q \ \mathrm {[C]} \ \)は，ワンポイント解説「1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係」の通り，
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ] \end{eqnarray}
\] であり，スイッチ\( \ \mathrm {S} \ \)投入後も合計の電荷量は変化しない。また，並列接続後の合成静電容量\( \ C^{\prime } \ \mathrm {[F]} \ \)は，ワンポイント解説「2.コンデンサの合成静電容量」の通り，
\[
\begin{eqnarray}
C^{\prime } &=&C+2C \\[ 5pt ] &=&3C \\[ 5pt ] \end{eqnarray}
\] であるため，並列接続後の全静電エネルギー\( \ W \ \mathrm {[J]} \ \)は，ワンポイント解説「3.コンデンサの静電エネルギー\( \ W \ \)」の通り，
\[
\begin{eqnarray}
W &=&\frac {Q^{2}}{2C^{\prime }} \\[ 5pt ] &=&\frac {\left( CV\right) ^{2}}{2\times 3C} \\[ 5pt ] &=&\frac {1}{6}CV^{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。