《理論》〈電子理論〉[R07上:問13]トランジスタの電流増幅率と出力インピーダンスに関する計算問題

【問題】

【難易度】★★★★★（難しい）

図はあるエミッタ接地トランジスタの静特性を示す。この特性より，ベース電流\( \ I_{\mathrm {B}}= 40 \ \mathrm {\mu A} \ \)，コレクタ･エミッタ間の電圧\( \ V_{\mathrm {CE}}= 6 \ \mathrm {V} \ \)における電流増幅率\( \ h_{\mathrm {fe}} \ \)（又は\( \ \beta \ \)）の値及び出力インピーダンス\( \ \displaystyle \frac {1}{h_{\mathrm {oe}}} \ \)（又は\( \ r_{0} \ \)）の値\( \ \mathrm {[\Omega ]} \ \)の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
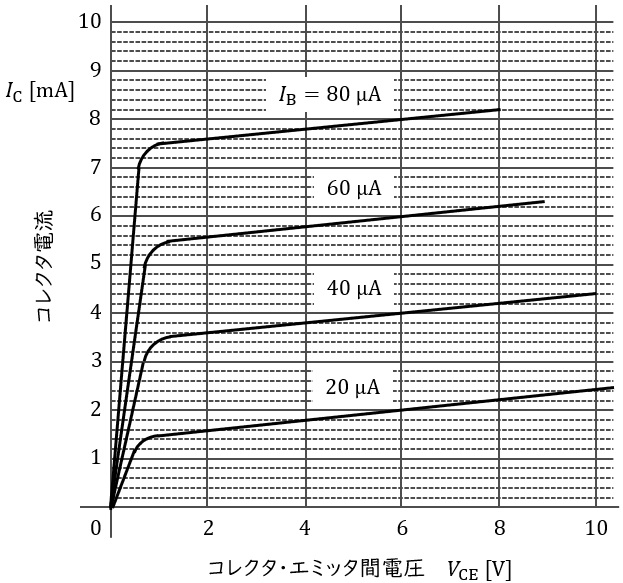
\begin{array}{ccc}
& h_{\mathrm {fe}} & \displaystyle \frac {1}{h_{\mathrm {oe}}} \\
\hline
(1) & 　80　 & 　30 \ 000　 \\
\hline
(2) & 　100　 & 　10 \ 000　 \\
\hline
(3) & 　100　 & 　20 \ 000　 \\
\hline
(4) & 　200　 & 　10 \ 000　 \\
\hline
(5) & 　200　 & 　20 \ 000　 \\
\hline
\end{array}
\]

【ワンポイント解説】

エミッタ接地トランジスタの静特性から\( \ h \ \)パラメータを導出する問題です。
電験での出題割合が少なく，しっかりと理解するためには電子回路の専門知識が必要となるため，かなり厳しい問題と言えます。電験対策としては，とりあえず本問が解けるようにしておけば十分でしょう。
本問は平成9年問13からの再出題となります。

1.トランジスタの基本式と\( \ h \ \)パラメータ
エミッタ接地回路の基本回路は図1に示すような回路で，入力にベース，出力にコレクタをとる信号増幅回路です。電圧電流とも増幅するため電力利得が高い増幅回路の基本となる回路で，電験でも最も出題されやすい回路となります。
交流信号に着目すると，トランジスタの入出力端子間の電圧電流において以下の式が成立し，これをトランジスタの基本式といいます。
\[
\begin{eqnarray}
v_{\mathrm {in}}&=&h_{\mathrm {ie}}i_{\mathrm {b}}+h_{\mathrm {re}}v_{\mathrm {out}} \\[ 5pt ] i_{\mathrm {c}}&=&h_{\mathrm {fe}}i_{\mathrm {b}}+h_{\mathrm {oe}}v_{\mathrm {out}} \\[ 5pt ] \end{eqnarray}
\] 上式の各計数を\( \ h \ \)パラメータといい，各パラメータの導出方法は以下の通りとなります。
\[
\begin{array}{|l|l|}
\hline
　　　h \ パラメータ & 　　　　導出式 \\
\hline
h_{\mathrm {ie}}（入力インピーダンス） & 　\displaystyle h_{\mathrm {ie}}=\left( \frac {v_{\mathrm {in}}}{i_{\mathrm {b}}}\right) _{v_{\mathrm {out}}=0}　 \\
\hline
h_{\mathrm {re}}（電圧帰還率）　 & 　\displaystyle h_{\mathrm {ie}}=\left( \frac {v_{\mathrm {in}}}{v_{\mathrm {out}}}\right) _{i_{\mathrm {b}}=0}　 \\
\hline
h_{\mathrm {fe}}（電流増幅率）　 & 　\displaystyle h_{\mathrm {fe}}=\left( \frac {i_{\mathrm {c}}}{i_{\mathrm {b}}}\right) _{v_{\mathrm {out}}=0}　 \\
\hline
h_{\mathrm {oe}}（出力アドミタンス）　 & 　\displaystyle h_{\mathrm {oe}}=\left( \frac {i_{\mathrm {c}}}{v_{\mathrm {out}}}\right) _{i_{\mathrm {b}}=0}　 \\
\hline
\end{array}
\]

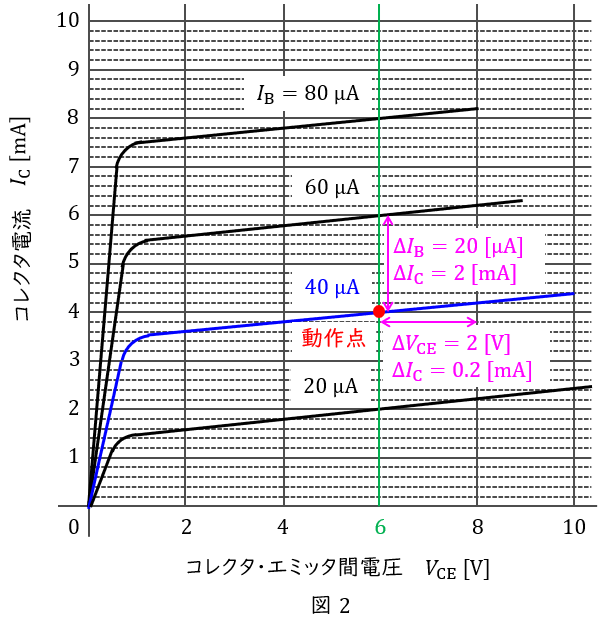
【解答】

解答：(2)
題意より，ベース電流\( \ I_{\mathrm {B}}= 40 \ \mathrm {\mu A} \ \)，コレクタ･エミッタ間の電圧\( \ V_{\mathrm {CE}}= 6 \ \mathrm {V} \ \)となっているので，動作点は図2に示す通りとなる。
ワンポイント解説「1.トランジスタの基本式と\( \ h \ \)パラメータ」の通り，電流増幅率\( \ h_{\mathrm {fe}} \ \)は，出力電圧の変化が零\( \ \left( V_{\mathrm {CE}}= 6 \ \mathrm {V} \right) \ \)におけるベース電流の変化量\( \ \Delta I_{\mathrm {B}} \ \)に対するコレクタ電流の変化量\( \ \Delta I_{\mathrm {C}} \ \)なので，図2より，
\[
\begin{eqnarray}
h_{\mathrm {fe}}&=&\frac {\Delta I_{\mathrm {C}}}{\Delta I_{\mathrm {B}}} \\[ 5pt ] &=&\frac {2\times 10^{-3}}{20\times 10^{-6}} \\[ 5pt ] &=&100 \\[ 5pt ] \end{eqnarray}
\] と求められる。また，出力インピーダンス\( \ \displaystyle \frac {1}{h_{\mathrm {oe}}} \ \)は，ベース電流の変化が零\( \ \left( I_{\mathrm {B}}= 40 \ \mathrm {\mu A} \right) \ \)におけるコレクタ電流の変化量\( \ \Delta I_{\mathrm {C}} \ \)に対する出力電圧の変化量\( \ \Delta V_{\mathrm {CE}} \ \)なので，図2より，
\[
\begin{eqnarray}
\frac {1}{h_{\mathrm {oe}}}&=&\frac {\Delta V_{\mathrm {CE}}}{\Delta I_{\mathrm {C}}} \\[ 5pt ] &=&\frac {2}{0.2\times 10^{-3}} \\[ 5pt ] &=&10 \ 000 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。