平成29年理論(問16)について，なぜΔ-Y変換すると静電容量が3倍になるのでしょうか。

【質問】

2017年理論(問16)(b)の静電容量\(C_{\mathrm {Y}}\)と\(C\)の関係が分かりません。何で\(3\)が入ってくるのでしょうか？
よろしくお願いします。

【回答】

ご質問ありがとうございました。
\(3\)が入ってくるのは\(\Delta – \mathrm {Y}\)変換をするからです。
ちなみに，なぜ設問において\(\Delta – \mathrm {Y}\)変換をするかというと，三相平衡回路を一相分等価回路にして計算しやすくするためです。

それでは何故\(\Delta – \mathrm {Y}\)変換をすると静電容量に\(3\)がくっついてくるのか説明します。
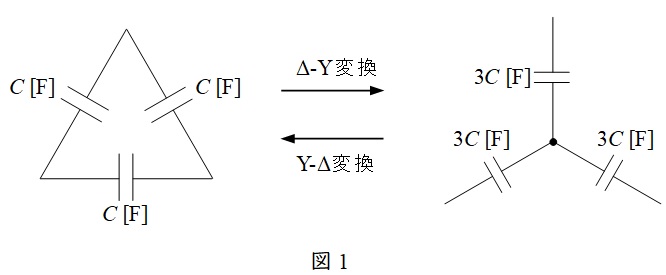
図1のように静電容量\(C\)の\(\Delta\)結線された回路について，等価変換したいと思います。
まず，それぞれのインピーダンス\(\dot Z\)は，角周波数を\(\omega \)とすると，
\[
\begin{eqnarray}
\dot Z&=&\frac {1}{j\omega C} \\[ 5pt ] \end{eqnarray}
\] となります。2017年理論(問16)(b)に掲載されている公式の通り\(\Delta – \mathrm {Y}\)変換をすると，\(\mathrm {Y}\)結線でのインピーダンス\(\dot Z_{\mathrm {Y}}\)は，
\[
\begin{eqnarray}
\dot Z_{\mathrm {Y}}&=&\frac {\dot Z\cdot \dot Z}{\dot Z+\dot Z+\dot Z} \\[ 5pt ] &=&\frac {\dot Z^{2}}{3\dot Z} \\[ 5pt ] &=&\frac {\dot Z}{3} \\[ 5pt ] \end{eqnarray}
\] となるので，\(\displaystyle \dot Z=\frac {1}{j\omega C}\)を代入すると，
\[
\begin{eqnarray}
\dot Z_{\mathrm {Y}}&=&\frac {1}{3}\dot Z \\[ 5pt ] &=&\frac {1}{3}\times \frac {1}{j\omega C}\\[ 5pt ] &=&\frac {1}{j\omega \left( 3C\right) } \\[ 5pt ] \end{eqnarray}
\] となるので，静電容量\(3C\)のインピーダンスと等しくなります。
よって，静電容量を\(\Delta – \mathrm {Y}\)変換すると値が\(3\)倍となります。