Contents
【問題】
【難易度】★★★☆☆(普通)
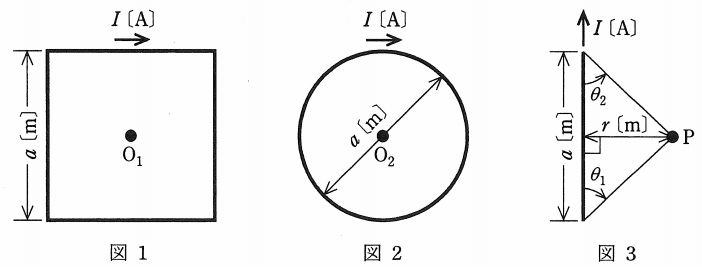
図1のように,\( \ 1 \ \)辺の長さが\( \ a \ \mathrm {[m]} \ \)の正方形のコイル(巻数:\( \ 1 \ \))に直流電流\( \ I \ \mathrm {[A]} \ \)が流れているときの中心点\( \ \mathrm {O}_{1} \ \)の磁界の大きさを\( \ H_{1} \ \mathrm {[A/m]} \ \)とする。また,図2のように,直径\( \ a \ \mathrm {[m]} \ \)の円形のコイル(巻数:\( \ 1 \ \))に直流電流\( \ I \ \mathrm {[A]} \ \)が流れているときの中心点\( \ \mathrm {O}_{2} \ \)の磁界の大きさを\( \ H_{2} \ \mathrm {[A/m]} \ \)とする。このとき,磁界の大きさの比\( \ \displaystyle \frac {H_{1}}{H_{2}} \ \)の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,中心点\( \ \mathrm {O}_{1} \ \),\( \ \mathrm {O}_{2} \ \)はそれぞれ正方形のコイル,円形のコイルと同一平面上にあるものとする。
参考までに,図3のように,長さ\( \ a \ \mathrm {[m]} \ \)の直線導体に直流電流\( \ I \ \mathrm {[A]} \ \)が流れているとき,導体から距離\( \ r \ \mathrm {[m]} \ \)離れた点\( \ \mathrm {P} \ \)における磁界の大きさ\( \ H \ \mathrm {[A/m]} \ \)は,\( \ \displaystyle H=\frac {I}{4\pi r}\left( \cos \theta _{1}+\cos \theta _{2} \right) \ \)で求められる(角度\( \ \theta _{1} \ \)と\( \ \theta _{2} \ \)の定義は図参照)。
(1) \( \ 0.45 \ \) (2) \( \ 0.90 \ \) (3) \( \ 1.00 \ \) (4) \( \ 1.11 \ \) (5) \( \ 2.22 \ \)
【ワンポイント解説】
正方形コイルと円形コイルの比較に関する問題です。
\( \ 3 \ \)種においては,円形コイルは公式として覚えておく必要がありますが,正方形コイルは積分計算を伴うため本問のように式を与えられると考えて問題ありません。
1.ビオ・サバールの法則
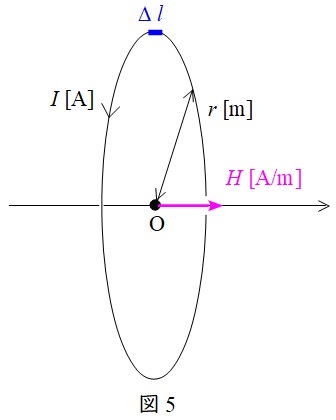
図4に示すように,微小な長さ\( \ \Delta l \ \)に流れる電流\( \ I \ \)が,距離\( \ r \ \)離れた場所に作る磁界\( \ \Delta H \ \)は,
\[
\begin{eqnarray}
\Delta H&=&\frac {I \Delta l}{4\pi r^{2}}\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
となります。

2.円形コイルが中心点に作る磁界の大きさ
ビオ・サバールの法則を図5のような円形コイルに適用すると,コイルの長さが\( \ 2 \pi r \ \)であり,中心点\( \ \mathrm {O} \ \)から見た微小電流の角度\( \ \theta \ \)は常に\( \ 90° \ \)であるから,
\[
\begin{eqnarray}
H&=&\frac {I \times 2\pi r}{4\pi r^{2}}\sin 90° \\[ 5pt ]
&=&\frac {I}{2r} \\[ 5pt ]
\end{eqnarray}
\]
となります。(この結果は公式として覚えておきましょう。)
【解答】
解答:(2)
題意より,図1の正方形のコイルの一辺が中心点\( \ \mathrm {O}_{1} \ \)に作る磁界の大きさ\( \ H_{1}^{\prime } \ \mathrm {[A/m]} \ \)は,
\[
\begin{eqnarray}
H_{1}^{\prime }&=&\frac {I}{\displaystyle 4\pi \cdot \frac {a}{2}}\left( \cos 45°+\cos 45° \right) \\[ 5pt ]
&=&\frac {I}{\displaystyle 2\pi a}\left( \frac {1}{\sqrt {2}}+ \frac {1}{\sqrt {2}} \right) \\[ 5pt ]
&=&\frac {I}{\displaystyle 2\pi a}\cdot \frac {2}{\sqrt {2}} \\[ 5pt ]
&=&\frac {I}{\displaystyle \sqrt {2} \pi a} \ \mathrm {[A/m]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,正方形コイルが中心点\( \ \mathrm {O}_{1} \ \)に作る磁界の大きさ\( \ H_{1} \ \mathrm {[A/m]} \ \)はその\( \ 4 \ \)倍であるから,
\[
\begin{eqnarray}
H_{1}&=&4H_{1}^{\prime } \\[ 5pt ]
&=&4\times \frac {I}{\displaystyle \sqrt {2}\pi a} \\[ 5pt ]
&=&\frac {2\sqrt {2}I}{\displaystyle \pi a} \ \mathrm {[A/m]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。一方,円形コイルが中心点\( \ \mathrm {O}_{2} \ \)に作る磁界の大きさ\( \ H_{2} \ \mathrm {[A/m]} \ \)は,ワンポイント解説「2.円形コイルが中心点に作る磁界の大きさ」の通り,
\[
\begin{eqnarray}
H_{2}&=&\frac {I}{2\cdot \displaystyle \frac {a}{2}} \\[ 5pt ]
&=&\frac {I}{a} \ \mathrm {[A/m]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,磁界の大きさの比\( \ \displaystyle \frac {H_{1}}{H_{2}} \ \)は,
\[
\begin{eqnarray}
\frac {H_{1}}{H_{2}}&=&\frac {\displaystyle \frac {2\sqrt {2}I}{\displaystyle \pi a}}{\displaystyle \frac {I}{a}} \\[ 5pt ]
&=&\frac {2\sqrt {2}}{\pi } \\[ 5pt ]
&≒&0.90 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは