《理論》〈電気及び電子計測〉[H27:問12]真空管を通る電子の運動に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

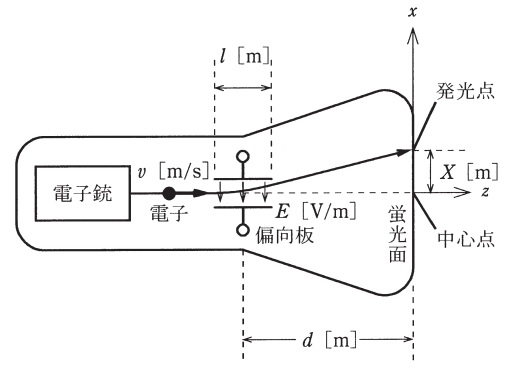
ブラウン管は電子銃，偏向板，蛍光面などから構成される真空管であり，オシロスコープの表示装置として用いられる。図のように，電荷\(-e \ \mathrm {[C]}\)をもつ電子が電子銃から一定の速度\(v \ \mathrm {[m/s]}\)で\(z\)軸に沿って発射される。電子は偏向板の中を通過する間，\(x\)軸に平行な平等電界\(E \ \mathrm {[V/m]}\)から静電力\(-eE \ \mathrm {[N]}\)を受け，\(x\)方向の速度成分\(u \ \mathrm {[m/s]}\)を与えられ進路を曲げられる。偏向板を通過後の電子は\(z\)軸と\(\displaystyle \tan \theta =\frac {u}{v}\)なる角度\(\theta \)をなす方向に直進して蛍光面に当たり，その点を発光させる。このとき発光する点は蛍光面の中心点から\(x\)方向に距離\(X \ \mathrm {[m]}\)だけシフトした点となる。

\(u\)と\(X\)を表す式の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

ただし，電子の静止質量を\(m \ \mathrm {[kg]}\)，偏向板の\(z\)方向の大きさを\(l \ \mathrm {[m]}\)，偏向板の中心から蛍光面までの距離を\(d \ \mathrm {[m]}\)とし，\(l ≪ d\)と仮定してよい。また，速度\(v\)は光速に比べて十分に小さいものとする。

\[
\begin{array}{ccc}
& 　　u　　 & 　　X　　 \\[5pt] \hline
(1) & 　　\displaystyle \frac {elE}{mv}　　 & 　　\displaystyle \frac {2eldE}{mv^{2}}　　 \\[5pt] \hline
(2) & 　　\displaystyle \frac {elE^{2}}{mv}　　 & 　　\displaystyle \frac {2eldE}{mv^{2}}　　 \\[5pt] \hline
(3) & 　　\displaystyle \frac {elE}{mv^{2}}　　 & 　　\displaystyle \frac {eldE^{2}}{mv}　　 \\[5pt] \hline
(4) & 　　\displaystyle \frac {elE^{2}}{mv^{2}}　　 & 　　\displaystyle \frac {eldE}{mv}　　 \\[5pt] \hline
(5) & 　　\displaystyle \frac {elE}{mv}　　 & 　　\displaystyle \frac {eldE}{mv^{2}}　　 \\[5pt] \hline
\end{array}
\]

【ワンポイント解説】

真空電子の運動に関する問題で，本問と全く同じような問題が何回か出題されています。解き方をよく理解して，同じ問題が出題されたら確実に得点できるようにしましょう。

1.運動方程式(力学)
質量\(m \ \mathrm {[kg]}\)の物体に\(F \ \mathrm {[N]}\)の力が加わった時の加速度\(a \ \mathrm {[m/s^{2}]}\)との関係は，
\[
F=ma
\] となります。

2.速度\(v\)と加速度\(a\)の関係(力学)
初速度が\(v_{0} \ \mathrm {[m/s]}\)の物体が加速度\(a \ \mathrm {[m/s^{2}]}\)で運動している時，\(t \ \mathrm {[s]}\) 後の物体の速度は
\[
v=v_{0}+at
\] となります。

【解答】

解答：(5)
題意に沿って，偏向板周辺部の模式図を描くと図1のようになる。

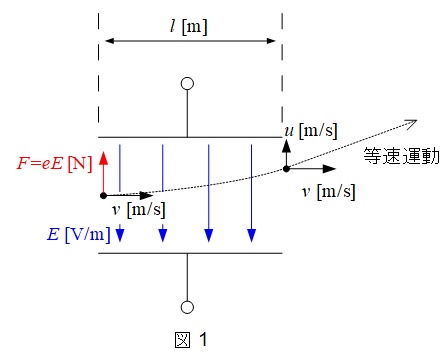
図1の通り，電子は\(z\)方向の速度成分は変化せず，\(x\)方向の速度成分のみ，静電力\(F=eE\)の大きさの力を受けることが分かる。よって，ワンポイント解説「1.運動方程式(力学)」の通り，電子に加わる\(x\)方向の加速度\(a\)は，
\[
\begin{eqnarray}
F&=&ma \\[ 5pt ] eE&=&ma \\[ 5pt ] a&=&\frac {eE}{m} \ \mathrm{[m/s^{2}]} \\[ 5pt ] \end{eqnarray}
\] となる。また，電界\(E\)が電子にかかる時間\(t_{1}\)は，\(z\)方向の速度成分は変化しないことから，
\[
t_{1}=\frac {l}{v} \ \mathrm{[s]}
\] となる。よって，偏向板から出た時の\(x\)方向の速度成分\(u\)は，ワンポイント解説「2.速度\(v\)と加速度\(a\)の関係(力学)」及び初速度が0であることから，
\[
\begin{eqnarray}
u&=&at_{1}\\[ 5pt ] &=&\frac {eE}{m}\cdot \frac {l}{v} \\[ 5pt ] a&=&\frac {elE}{mv} \ \mathrm{[m/s]} \\[ 5pt ] \end{eqnarray}
\] と求められる。
次に偏向板を出てから，蛍光面に到達するまで，電子は等速直線運動をする。偏向板を出てから蛍光面へ到達するまでの時間\(t_{2}\)は，
\[
\begin{eqnarray}
t_{2}&=&\frac {d-\frac {l}{2}}{v} \\[ 5pt ] &≒&\frac {d}{v} \ \mathrm{[s]} (d ≫ l)
\end{eqnarray}
\] であるから，偏向板内の\(x\)方向の移動は十分に小さいので，発光する点の中心からの距離\(X\)は，
\[
\begin{eqnarray}
X&=&ut_{2} \\[ 5pt ] &=&\frac {eE}{m}\cdot \frac {l}{v}t_2 \\[ 5pt ] &=&\frac {elE}{mv}\frac {d}{v} \\[ 5pt ] &=&\frac {eldE}{mv^{2}} \ \mathrm{[m]} \\[ 5pt ] \end{eqnarray}
\] と求められる。