《機械》〈変圧器〉[H23:問7]変圧器の損失と効率の特性に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，変圧器の損失と効率に関する記述である。

電圧一定で出力を変化させても，出力一定で電圧を変化させても，変圧器の効率の最大は鉄損と銅損とが等しいときに生じる。ただし，変圧器の損失は鉄損と銅損だけとし，負荷の力率は一定とする。

a.出力$\ 1 \ 000 \ \mathrm {[W]} \ $で運転している単相変圧器において鉄損が$\ 40.0 \ \mathrm {[W]} \ $，銅損が$\ 40.0 \ \mathrm {[W]} \ $発生している場合，変圧器の効率は$\ \fbox {　 （ア） 　} \ \mathrm {[％]} \ $である。

b.出力電圧一定で出力を$\ 500 \ \mathrm {[W]} \ $に下げた場合の鉄損は$\ 40.0 \ \mathrm {[W]} \ $，銅損は$\ \fbox {　 （イ） 　} \ \mathrm {[W]} \ $，効率は$\ \fbox {　 （ウ） 　} \ \mathrm {[％]} \ $となる。

c.出力電圧が$\ 20 \ \mathrm {[％]} \ $低下した状態で，出力$\ 1 \ 000 \ \mathrm {[W]} \ $の運転をしたとすると鉄損は$\ 25.6 \ \mathrm {[W]} \ $，銅損は$\ \fbox {　 （エ） 　} \ \mathrm {[W]} \ $，効率は$\ \fbox {　 （オ） 　} \ \mathrm {[％]} \ $となる。ただし，鉄損は電圧の$\ 2 \ $乗に比例するものとする。

上記の記述中の空白箇所(ア)，(イ)，(ウ)，(エ)及び(オ)に当てはまる最も近い数値の組合せを，次の(1)～(5)のうちから一つ選べ。

$$\begin{array}{cccccc} & （ア） & （イ） & （ウ） & （エ） & （オ） \\ \hline (1) & 　94　 & 　20.0　 & 　89　 & 　61.5　 & 　91　 \\ \hline (2) & 　93　 & 　10.0　 & 　91　 & 　62.5　 & 　92　 \\ \hline (3) & 　94　 & 　20.0　 & 　89　 & 　63.5　 & 　91　 \\ \hline (4) & 　93　 & 　10.0　 & 　91　 & 　50.0　 & 　93　 \\ \hline (5) & 　92　 & 　20.0　 & 　89　 & 　61.5　 & 　91　 \\ \hline \end{array}$$

【ワンポイント解説】

変圧器の損失に関する問題です。
a.およびb.の内容は標準的かやや易しいレベルの内容ですが，c.の文章が加わることでぐんと難易度が上がっている問題です。
メカニズムを一度理解すれば忘れにくい内容なので，確実に理解するようにしましょう。

1.変圧器の等価回路（一次換算）と鉄損及び銅損
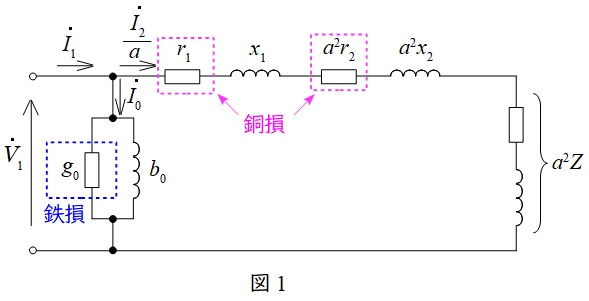
変圧器の一次側換算等価回路を図1に示します。ただし，$\ {\dot V}_{1} \ $は一次側端子電圧，$\ {\dot I}_{1} \ $は一次電流，$\ {\dot I}_{2} \ $は二次電流，$\ {\dot I}_{0} \ $は励磁電流，$\ r_{1} \ $は一次巻線抵抗，$\ r_{2} \ $は二次巻線抵抗，$\ x_{1} \ $は一次漏れリアクタンス，$\ x_{2} \ $は二次漏れリアクタンス，$\ a \ $は変圧比（巻数比）となります。
等価回路より，鉄損は電圧$\ {\dot V}_{1} \ $の$\ 2 \ $乗に比例し，銅損は電流$\ {\dot I}_{2} \ $の$\ 2 \ $乗に比例することがわかります。

2.変圧器の効率$\ \eta \ $と最大効率$\ \eta _{\mathrm {m}} \ $
変圧器の損失は鉄損$\ p_{\mathrm {i}} \ $と銅損$\ p_{\mathrm {c}} \ $があり，$\ p_{\mathrm {i}} \ $は負荷によらず一定であり，$\ p_{\mathrm {c}} \ $は負荷(電流)の$\ 2 \ $乗に比例します。従って，定格出力$\ P_{\mathrm {n}} \ $で利用率$\ \alpha \ $の時の変圧器の効率$\ \eta \ $は，
$$\begin{eqnarray} \eta &=&\frac {出力}{入力} \\[ 5pt ] &=&\frac {出力}{出力+損失} \\[ 5pt ] &=&\frac {\alpha P_{\mathrm {n}}}{\alpha P_{\mathrm {n}}+p_{\mathrm {i}}+\alpha ^{2}p_{\mathrm {c}}} \\[ 5pt ] \end{eqnarray}$$ となります。
次に，最大効率$\ \eta _{\mathrm {m}} \ $を求めます。上式の分母分子を$\ \alpha \ $で割ると
$$\begin{eqnarray} \eta &=&\frac {P_{\mathrm {n}}}{\displaystyle P_{\mathrm {n}}+\frac {p_{\mathrm {i}}}{\alpha }+\alpha p_{\mathrm {c}}} \\[ 5pt ] \end{eqnarray}$$ となり，効率が最大となるためには，上式の分母が最小となれば良いです。よって，$\ \displaystyle A=P_{\mathrm {n}}+\frac {p_{\mathrm {i}}}{\alpha }+\alpha p_{\mathrm {c}} \ $と置くと，
$$\begin{eqnarray} \frac {\mathrm {d}A}{\mathrm {d}\alpha }&=&-\frac {p_{\mathrm {i}}}{\alpha ^{2} }+p_{\mathrm {c}} \\[ 5pt ] \end{eqnarray}$$ となります。よって$\ \displaystyle \frac {\mathrm {d}A}{\mathrm {d}\alpha }=0 \ $となるとき，$\ p_{\mathrm {i}}=\alpha ^{2}p_{\mathrm {c}} \ $であり，鉄損と銅損が等しい時効率は最大となります。

　※　電験$\ 3 \ $種においては，鉄損と銅損が等しい時，効率が最大となることを覚えていれば問題ありません。

【関連する「電気の神髄」記事】

　　変圧器の効率

【解答】

解答：(2)
(ア)
ワンポイント解説「2.変圧器の効率$\ \eta \ $と最大効率$\ \eta _{\mathrm {m}} \ $」の通り，出力$\ P_{\mathrm {o}}=1 \ 000 \ \mathrm {[W]} \ $，鉄損$\ p_{\mathrm {i}}=40.0 \ \mathrm {[W]} \ $，銅損$\ p_{\mathrm {c}}=40.0 \ \mathrm {[W]} \ $の時の効率$\ \eta \ $は，
$$\begin{eqnarray} \eta &=&\frac {P_{\mathrm {o}}}{\displaystyle P_{\mathrm {o}}+p_{\mathrm {i}}+p_{\mathrm {c}}} \\[ 5pt ] &=&\frac {1000}{\displaystyle 1000+40+40} \\[ 5pt ] &≒&0.9259　→　93 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(イ)
銅損は出力の$\ 2 \ $乗に比例に比例するので，出力$\ P_{\mathrm {o}}^{\prime }=500 \ \mathrm {[W]} \ $の時の銅損$\ p_{\mathrm {c}}^{\prime } \ \mathrm {[W]} \ $は，
$$\begin{eqnarray} p_{\mathrm {c}}^{\prime } &=&\left( \frac {500}{1000}\right) ^{2}\times p_{\mathrm {c}} \\[ 5pt ] &=&\frac {1}{4}\times 40 \\[ 5pt ] &=&10 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(ウ)
（イ）より，出力$\ P_{\mathrm {o}}^{\prime }=500 \ \mathrm {[W]} \ $の時の効率$\ \eta ^{\prime } \ $は，
$$\begin{eqnarray} \eta ^{\prime }&=&\frac {P_{\mathrm {o}}^{\prime }}{\displaystyle P_{\mathrm {o}}^{\prime }+p_{\mathrm {i}}+p_{\mathrm {c}}^{\prime }} \\[ 5pt ] &=&\frac {500}{\displaystyle 500+40+10} \\[ 5pt ] &≒&0.9091　→　91 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(エ)
単相変圧器の出力$\ P_{\mathrm {o}} \ \mathrm {[W]} \ $は，電圧$\ V \ \mathrm {[V]}$，電流$\ I \ \mathrm {[A]}$，力率$\ \cos \theta$を用いて，
$$\begin{eqnarray} P_{\mathrm {o}}&=&VI\cos \theta \\[ 5pt ] \end{eqnarray}$$ で与えられ，これより，
$$\begin{eqnarray} I&=&\frac {P_{\mathrm {o}}}{V\cos \theta } \\[ 5pt ] \end{eqnarray}$$ となる。出力及び力率一定で電圧が$\ 20 \ \mathrm {[％]} \ $低下したときの電流$\ I^{\prime } \ \mathrm {[A]}$は，
$$\begin{eqnarray} I^{\prime }&=&\frac {P_{\mathrm {o}}}{0.8V\cos \theta } \\[ 5pt ] &=&\frac {I}{0.8} \\[ 5pt ] &=&1.25I \\[ 5pt ] \end{eqnarray}$$ となるので，このときの銅損$\ p_{\mathrm {c}}^{\prime \prime } \ \mathrm {[W]} \ $は，
$$\begin{eqnarray} p_{\mathrm {c}}^{\prime \prime } &=&\left( \frac {1.25I}{I}\right) ^{2}\times p_{\mathrm {c}} \\[ 5pt ] &=&1.5625\times 40 \\[ 5pt ] &=&62.5 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(オ)
（エ）より，出力電圧が$\ 20 \ \mathrm {[％]} \ $低下した状態での効率$\ \eta ^{\prime \prime } \ $は，鉄損$\ p_{\mathrm {i}}^{\prime \prime }=0.8^{2}\times 40 =25.6 \ \mathrm {[W]} \ $が与えられているので，
$$\begin{eqnarray} \eta ^{\prime \prime }&=&\frac {P_{\mathrm {o}}}{\displaystyle P_{\mathrm {o}}+p_{\mathrm {i}}^{\prime \prime }+p_{\mathrm {c}}^{\prime \prime }} \\[ 5pt ] &=&\frac {1000}{\displaystyle 1000+25.6+62.5} \\[ 5pt ] &≒&0.9190　→　92 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}$$ と求められる。