【問題】
【難易度】★★★☆☆(普通)
次の文章は,単相半波ダイオード整流回路に関する記述である。
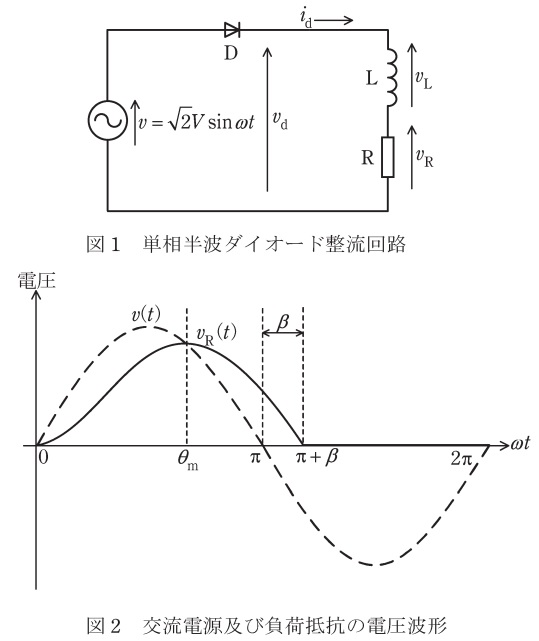
抵抗\( \ \mathrm {R} \ \)とリアクトル\( \ \mathrm {L} \ \)とを直列接続した負荷に電力を供給する単相半波ダイオード整流回路を図1に示す。また図1に示した回路の交流電源の電圧波形\( \ v\left( t \right) \ \)を破線で,抵抗\( \ \mathrm {R} \ \)の電圧波形\( \ v_{\mathrm {R}}\left( t \right) \ \)を実線で図2に示す。ただし,ダイオード\( \ \mathrm {D} \ \)の電圧降下及びリアクトル\( \ \mathrm {L} \ \)の抵抗は無視する。次の(a)及び(b)の問に答えよ。
ただし,必要であれば次の計算結果を利用してよい。
\[
\begin{eqnarray}
\int ^{\alpha } _{0}\sin \theta \mathrm {d}\theta &=&1-\cos \alpha \\[ 5pt ]
\int ^{\alpha } _{0}\cos \theta \mathrm {d}\theta &=&\sin \alpha \\[ 5pt ]
\end{eqnarray}
\]
(a) 以下の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
図1の電源電圧\( \ v\left( t \right) \gt 0 \ \)の期間においてダイオード\( \ \mathrm {D} \ \)は順方向バイアスとなり導通する。\( \ v\left( t \right) \ \)と\( \ v_{\mathrm {R}}\left( t \right) \ \)が等しくなる電源電圧\( \ v\left( t \right) \ \)の位相を\( \ \omega t=\theta _{\mathrm {m}} \ \)とすると,出力電流\( \ i_{\mathrm {d}}\left( t \right) \ \)が増加する電源電圧の位相\( \ \omega t \ \)が\( \ 0 \lt \omega t \lt \theta _{\mathrm {m}} \ \)の期間においては\( \ \fbox { (ア) } \ \),\( \ \omega t = \theta _{\mathrm {m}} \ \)以降については\( \ \fbox { (イ) } \ \)となる。出力電流\( \ i_{\mathrm {d}}\left( t \right) \ \)は電源電圧\( \ v\left( t \right) \ \)が負となっても\( \ v\left( t \right) =0 \ \)の点よりも\( \ \omega t=\beta \ \)に相当する時間だけ長く流れ続ける。すなわち,\( \ \mathrm {L} \ \)の磁気エネルギーが\( \ \fbox { (ウ) } \ \)となる\( \ \omega t=\pi +\beta \ \)で出力電流\( \ i_{\mathrm {d}}\left( t \right) \ \)が\( \ 0 \ \)となる。出力電圧\( \ v_{\mathrm {d}}\left( t \right) \ \)の平均値\( \ V_{\mathrm {d}} \ \)は電源電圧\( \ v\left( t \right) \ \)を\( \ 0 \sim \ \fbox { (エ) } \ \)の区間で積分して一周期である\( \ 2\pi \ \)で除して計算でき,このとき\( \ \mathrm {L} \ \)の電圧\( \ v_{\mathrm {L}}\left( t \right) \ \)を同区間で積分すれば\( \ 0 \ \)となるので,\( \ V_{\mathrm {d}} \ \)は抵抗\( \ \mathrm {R} \ \)の電圧\( \ v_{\mathrm {R}}\left( t \right) \ \)の平均値\( \ V_{\mathrm {R}} \ \)に等しくなる。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & v_{\mathrm {L}}\left( t \right) \gt 0 & v_{\mathrm {L}}\left( t \right) \lt 0 & 0 & \pi +\beta \\
\hline
(2) & v_{\mathrm {L}}\left( t \right) \lt 0 & v_{\mathrm {L}}\left( t \right) \gt 0 & 0 & \pi +\beta \\
\hline
(3) & v_{\mathrm {L}}\left( t \right) \gt 0 & v_{\mathrm {L}}\left( t \right) \lt 0 & 最大 & \pi +\beta \\
\hline
(4) & v_{\mathrm {L}}\left( t \right) \lt 0 & v_{\mathrm {L}}\left( t \right) \gt 0 & 最大 & \beta \\
\hline
(5) & v_{\mathrm {L}}\left( t \right) \gt 0 & v_{\mathrm {L}}\left( t \right) \lt 0 & 0 & \beta \\
\hline
\end{array}
\]
(b) 小問(a)において,電源電圧の実効値\( \ 100 \ \mathrm {V} \ \),\( \ \displaystyle \beta =\frac {\pi }{6} \ \)のときの出力電圧\( \ v_{\mathrm {d}}\left( t \right) \ \)の平均値\( \ V_{\mathrm {d}} \ \mathrm {[V]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 3 \ \) (2) \( \ 20 \ \) (3) \( \ 42 \ \) (4) \( \ 45 \ \) (5) \( \ 90 \ \)
【ワンポイント解説】
単相半波整流回路に関する問題です。
単相半波整流回路は単相全波整流回路や三相整流回路の基本となる内容です。
各タイミングでどのような動作をするかイメージして理解するようにしましょう。
1.リアクトルを含む単相半波ダイオード整流回路の動作
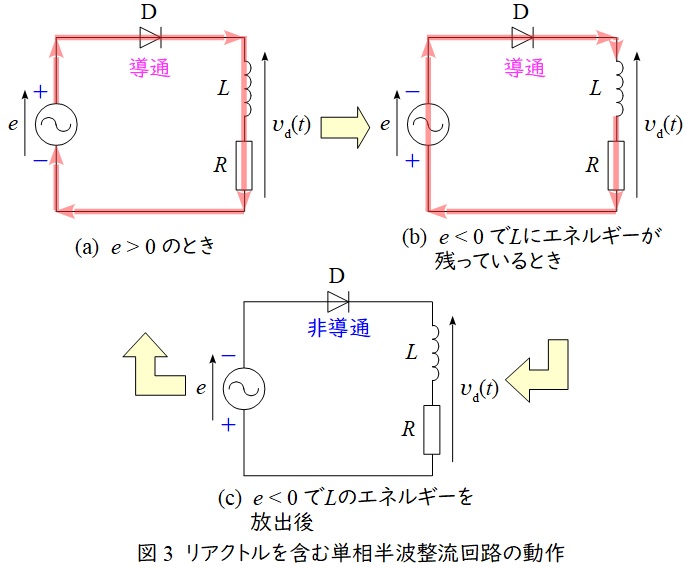
単相半波ダイオード整流回路の動作を図3に示します。
正弦波の電源電圧\( \ e \gt 0 \ \)のときは,(a)のようにダイオード\( \ \mathrm {D} \ \)が導通するため,出力側に電流が流れます。その際,リアクトル\( \ \mathrm {L} \ \)にエネルギーが蓄えられます。
電源電圧が\( \ e \lt 0 \ \)に切り換わると,(b)のように電源からはダイオード\( \ \mathrm {D} \ \)に対し逆方向の電圧がかかりますが,リアクトル\( \ \mathrm {L} \ \)に蓄えられているエネルギーがあるため,リアクトル\( \ \mathrm {L} \ \)から電源側に電流が流れます。
電源電圧が\( \ e \lt 0 \ \)に切り換わり,リアクトル\( \ \mathrm {L} \ \)にエネルギーがなくなると,(c)のようにダイオード\( \ \mathrm {D} \ \)に対し逆方向の電圧がかかるようになるため\( \ \mathrm {D} \ \)が導通せず,電流は流れなくなります。
以後,(a)~(c)を繰り返すようになります。
【関連する「電気の神髄」記事】
【解答】
(a)解答:(1)
(ア)
\( \ v_{\mathrm {L}}\left( t \right) =v\left( t \right) -v_{\mathrm {R}}\left( t \right) \ \)の関係があるので,\( \ 0 \lt \omega t \lt \theta _{\mathrm {m}} \ \)の期間においては図2より,\( \ v_{\mathrm {L}}\left( t \right) \gt 0 \ \)となります。
(イ)
(ア)と同様,\( \ v_{\mathrm {L}}\left( t \right) =v\left( t \right) -v_{\mathrm {R}}\left( t \right) \ \)の関係があるので,\( \ \omega t = \theta _{\mathrm {m}} \ \)以降においては図2より,\( \ v_{\mathrm {L}}\left( t \right) \lt 0 \ \)となります。
(ウ)
ワンポイント解説「1.リアクトルを含む単相半波ダイオード整流回路の動作」の通り,\( \ \omega t=\pi +\beta \ \)でリアクトルはエネルギーを放出し終えるため,エネルギーは\( \ 0 \ \)となります。
(エ)
出力電圧\( \ v_{\mathrm {d}}\left( t \right) \ \)の平均値\( \ V_{\mathrm {d}} \ \)は,導通している間の電源電圧\( \ v\left( t \right) \ \)の平均値となるため,\( \ 0 \sim \pi +\beta \ \)の区間で積分して一周期である\( \ 2\pi \ \)で除して計算することにより求めることができます。
(b)解答:(3)
(a)の(エ)に関して式に表すと,
\[
\begin{eqnarray}
V_{\mathrm {d}} &=&\frac {1}{2\pi}\int _{0}^{\pi +\beta }v\left( t \right) \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {1}{2\pi}\int _{0}^{\pi +\beta }\sqrt {2} V \sin \omega t \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {\sqrt {2} V}{2\pi} \int _{0}^{\pi +\beta }\sin \omega t \mathrm {d}\omega t \\[ 5pt ]
\end{eqnarray}
\]
となるから,題意より,
\[
\begin{eqnarray}
\int ^{\alpha } _{0}\sin \theta \mathrm {d}\theta &=&1-\cos \alpha \\[ 5pt ]
\end{eqnarray}
\]
を適用すると,
\[
\begin{eqnarray}
V_{\mathrm {d}} &=&\frac {\sqrt {2} V}{2\pi} \left\{ 1-\cos \left( \pi +\beta \right) \right\} \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ V=100 \ \mathrm {[V]} \ \),\( \ \displaystyle \beta =\frac {\pi }{6} \ \)を代入すると,
\[
\begin{eqnarray}
V_{\mathrm {d}} &=&\frac {\sqrt {2} \times 100}{2\pi} \left\{ 1-\cos \left( \pi +\frac {\pi }{6} \right) \right\} \\[ 5pt ]
&=&\frac {100\sqrt {2}}{2\pi } \left( 1-\cos \frac {7\pi }{6} \right) \\[ 5pt ]
&=&\frac {50\sqrt {2}}{\pi } \left( 1+\frac {\sqrt {3}}{2} \right) \\[ 5pt ]
&≒&42.0 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは