《理論》〈電子理論〉[R4上:問18]トランジスタ増幅器のバイアス回路に関する計算・空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

図1，図2及び図3は，トランジスタ増幅器のバイアス回路を示す。次の(a)及び(b)の問に答えよ。

ただし，\( \ V_{\mathrm {CC}} \ \)は電源電圧，\( \ V_{\mathrm {B}} \ \)はベース電圧，\( \ I_{\mathrm {B}} \ \)はベース電流，\( \ I_{\mathrm {C}} \ \)はコレクタ電流，\( \ I_{\mathrm {E}} \ \)はエミッタ電流，\( \ R \ \)，\( \ R_{\mathrm {B}} \ \)，\( \ R_{\mathrm {C}} \ \)及び\( \ R_{\mathrm {E}} \ \)は抵抗を示す。

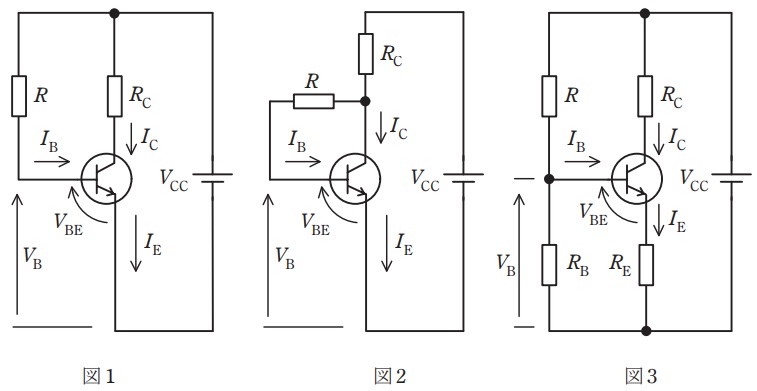
(a)　次の①式，②式及び③式は，図1，図2及び図3のいずれかの回路のベース・エミッタ間の電圧\( \ V_{\mathrm {BE}} \ \)を示す。
\[
\begin{eqnarray}
V_{\mathrm {BE}} &=&V_{\mathrm {B}}-I_{\mathrm {E}}\cdot R_{\mathrm {E}}　　　&・・・・・・・・・・　①& \\[ 5pt ] V_{\mathrm {BE}} &=&V_{\mathrm {CC}}-I_{\mathrm {B}}\cdot R　　　&・・・・・・・・・・　②& \\[ 5pt ] V_{\mathrm {BE}} &=&V_{\mathrm {CC}}-I_{\mathrm {B}}\cdot R-I_{\mathrm {E}}\cdot R_{\mathrm {C}}　　　&・・・・・・・・・・　③& \\[ 5pt ] \end{eqnarray}
\] 上記の式と図の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{cccc}
& ①式 & ②式 & ③式 \\
\hline
(1) & 　　図 \ 1　　 & 　　図 \ 2　　 & 　　図 \ 3　　 \\
\hline
(2) & 　　図 \ 2　　 & 　　図 \ 3　　 & 　　図 \ 1　　 \\
\hline
(3) & 　　図 \ 3　　 & 　　図 \ 1　　 & 　　図 \ 2　　 \\
\hline
(4) & 　　図 \ 1　　 & 　　図 \ 3　　 & 　　図 \ 2　　 \\
\hline
(5) & 　　図 \ 3　　 & 　　図 \ 2　　 & 　　図 \ 1　　 \\
\hline
\end{array}
\]

(b) 次の文章ａ，ｂ及びｃは，それぞれのバイアス回路における周囲温度の変化と電流\( \ I_{\mathrm {C}} \ \)との関係について述べたものである。
ただし，\( \ h_{\mathrm {FE}} \ \)は直流電流増幅率を表す。

ａ　温度上昇により\( \ h_{\mathrm {FE}} \ \)が増加すると\( \ I_{\mathrm {C}} \ \)が増加し，バイアス安定度が悪いバイアス回路の図は\( \ \fbox {　（ア）　} \ \)である。

ｂ　\( \ h_{\mathrm {FE}} \ \)の変化により\( \ I_{\mathrm {C}} \ \)が増加しようとすると，\( \ V_{\mathrm {B}} \ \)はほぼ一定であるから\( \ V_{\mathrm {BE}} \ \)が減少するので，\( \ I_{\mathrm {C}} \ \)や\( \ I_{\mathrm {E}} \ \)の増加を妨げるように働く。\( \ I_{\mathrm {C}} \ \)の変化の割合が比較的低く，バイアス安定度が良いものの，電力損失が大きいバイアス回路の図は\( \ \fbox {　（イ）　} \ \)である。

ｃ　\( \ h_{\mathrm {FE}} \ \)の変化により\( \ I_{\mathrm {C}} \ \)が増加しようとすると，\( \ R_{\mathrm {C}} \ \)の電圧降下も増加することでコレクタ・エミッタ間の電圧\( \ V_{\mathrm {CE}} \ \)が低下する。これにより\( \ R \ \)の電圧が減少して\( \ I_{\mathrm {B}} \ \)が減少するので，\( \ I_{\mathrm {C}} \ \)の増加が抑えられるバイアス回路の図は\( \ \fbox {　（ウ）　} \ \)である。

上記の記述中の空白箇所(ア)～(ウ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{cccc}
& ①式 & ②式 & ③式 \\
\hline
(1) & 　　図 \ 1　　 & 　　図 \ 2　　 & 　　図 \ 3　　 \\
\hline
(2) & 　　図 \ 2　　 & 　　図 \ 3　　 & 　　図 \ 1　　 \\
\hline
(3) & 　　図 \ 3　　 & 　　図 \ 1　　 & 　　図 \ 2　　 \\
\hline
(4) & 　　図 \ 1　　 & 　　図 \ 3　　 & 　　図 \ 2　　 \\
\hline
(5) & 　　図 \ 2　　 & 　　図 \ 1　　 & 　　図 \ 3　　 \\
\hline
\end{array}
\]

【ワンポイント解説】

バイポーラトランジスタのバイアス回路に関する問題です。
図1が固定バイアス回路，図2が自己バイアス回路，図3が電流帰還バイアス回路と呼ばれます。いずれも電子回路の教科書には掲載されている内容ですが，名称よりも定性的なメカニズムを理解するようにして下さい。

1.バイポーラトランジスタのバイアス回路
①固定バイアス回路
問題の図1に示す回路となります。
バイアス回路の中で最も単純な構成の回路ですが，温度上昇により\( \ h_{\mathrm {FE}} \ \)が増加すると\( \ I_{\mathrm {C}} \ \)が増加し，バイアス安定度が悪くなる特徴があります。
定量的には以下の通りとなります。
\( \ V_{\mathrm {CC}} \ \)→\( \ R \ \)→トランジスタ→\( \ V_{\mathrm {CC}} \ \)の閉回路において，
\[
\begin{eqnarray}
V_{\mathrm {CC}}&=&RI_{\mathrm {B}}+V_{\mathrm {BE}} \\[ 5pt ] RI_{\mathrm {B}}&=&V_{\mathrm {CC}}-V_{\mathrm {BE}} \\[ 5pt ] I_{\mathrm {B}}&=&\frac {V_{\mathrm {CC}}-V_{\mathrm {BE}}}{R} \\[ 5pt ] \end{eqnarray}
\] であり，バイポーラトランジスタにおいては\( \ V_{\mathrm {BE}} \ \)は一定として扱い，\( \ V_{\mathrm {CC}} \ \)，\( \ R \ \)も一定なので，\( \ I_{\mathrm {B}} \ \)は一定となります。
したがって，コレクタ電流\( \ I_{\mathrm {C}} \ \)は，トランジスタの電流増幅率を\( \ h_{\mathrm {FE}} \ \)とすると，
\[
\begin{eqnarray}
I_{\mathrm {C}}&=&h_{\mathrm {FE}}I_{\mathrm {B}} \\[ 5pt ] \end{eqnarray}
\] となるので，トランジスタの動作点が変わり，場合によっては交流信号の波形がひずむ可能性があります。

②自己バイアス回路
問題の図2に示すような回路となります。
温度上昇により\( \ h_{\mathrm {FE}} \ \)が増加しても\( \ I_{\mathrm {C}} \ \)の上昇を抑えられる回路です。
定量的には以下の通りとなります。
\( \ V_{\mathrm {CC}} \ \)→\( \ R_{\mathrm {C}} \ \)→\( \ R \ \)→トランジスタ→\( \ V_{\mathrm {CC}} \ \)の閉回路において，
\[
\begin{eqnarray}
V_{\mathrm {CC}}&=&V_{\mathrm {BE}}+RI_{\mathrm {B}}+R_{\mathrm {C}}\left( I_{\mathrm {B}}+I_{\mathrm {C}}\right) \\[ 5pt ] \end{eqnarray}
\] となり，\( \ I_{\mathrm {C}}≫I_{\mathrm {B}} \ \)より，
\[
\begin{eqnarray}
V_{\mathrm {CC}}&≃&V_{\mathrm {BE}}+RI_{\mathrm {B}}+R_{\mathrm {C}}I_{\mathrm {C}} \\[ 5pt ] RI_{\mathrm {B}}&=&V_{\mathrm {CC}}-V_{\mathrm {BE}}-R_{\mathrm {C}}I_{\mathrm {C}} \\[ 5pt ] I_{\mathrm {B}}&=&\frac {V_{\mathrm {CC}}-V_{\mathrm {BE}}-R_{\mathrm {C}}I_{\mathrm {C}}}{R} \\[ 5pt ] \end{eqnarray}
\] となるので，仮に\( \ h_{\mathrm {FE}} \ \)が変化し\( \ I_{\mathrm {C}} \ \)が上昇しても上式により\( \ I_{\mathrm {B}} \ \)が低下することになり，結果的に\( \ I_{\mathrm {C}} \ \)の上昇が抑えられることになります。

③電流帰還バイアス回路
問題の図3に示す回路となります。
\( \ I_{\mathrm {C}} \ \)の変化の割合が比較的低く，バイアスの安定度が良いですが，\( \ R_{\mathrm {B}} \ \)に流す電流の分，電力損失が大きいバイアス回路となります。
定量的には以下の通りとなります。
ベース電流\( \ I_{\mathrm {B}} \ \)は十分に小さいとすると，ベース電位\( \ V_{\mathrm {B}} \ \)は，分圧の法則より，
\[
\begin{eqnarray}
V_{\mathrm {B}}&=&\frac {R_{\mathrm {B}}}{R+R_{\mathrm {B}}}V_{\mathrm {CC}}\\[ 5pt ] \end{eqnarray}
\] となり，ほぼ一定となります。これより，エミッタ電流\( \ I_{\mathrm {E}} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {E}}&=&\frac {V_{\mathrm {B}}-V_{\mathrm {BE}}}{R_{\mathrm {E}}} \\[ 5pt ] \end{eqnarray}
\] となり，上式を変形すると，
\[
\begin{eqnarray}
R_{\mathrm {E}}I_{\mathrm {E}}&=&V_{\mathrm {B}}-V_{\mathrm {BE}} \\[ 5pt ] V_{\mathrm {BE}}&=&V_{\mathrm {B}}-R_{\mathrm {E}}I_{\mathrm {E}} \\[ 5pt ] &≃&V_{\mathrm {B}}-R_{\mathrm {E}}I_{\mathrm {C}} \\[ 5pt ] \end{eqnarray}
\] となります。この式より，仮に\( \ h_{\mathrm {FE}} \ \)が変化し\( \ I_{\mathrm {C}} \ \)が上昇しても\( \ V_{\mathrm {BE}} \ \)が減少するので\( \ I_{\mathrm {B}} \ \)が低下するというバイアスがかかることになります。

【解答】

(a)解答：(3)
図1-1に示す閉回路において，回路方程式は，
\[
\begin{eqnarray}
V_{\mathrm {CC}}&=&V_{\mathrm {BE}}+RI_{\mathrm {B}} \\[ 5pt ] V_{\mathrm {BE}}&=&V_{\mathrm {CC}}-RI_{\mathrm {B}} \\[ 5pt ] \end{eqnarray}
\] となり，②式に該当する。

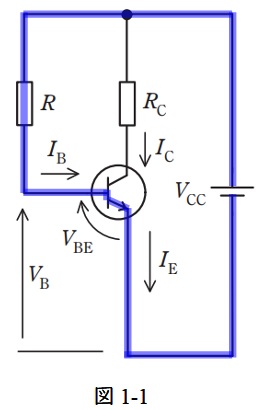
図2-1に示す閉回路において，回路方程式は，
\[
\begin{eqnarray}
V_{\mathrm {CC}}&=&V_{\mathrm {BE}}+RI_{\mathrm {B}}+R_{\mathrm {C}}\left( I_{\mathrm {B}}+I_{\mathrm {C}}\right) \\[ 5pt ] &=&V_{\mathrm {BE}}+RI_{\mathrm {B}}+R_{\mathrm {C}}I_{\mathrm {E}} \\[ 5pt ] V_{\mathrm {BE}}&=&V_{\mathrm {CC}}-RI_{\mathrm {B}}-R_{\mathrm {C}}I_{\mathrm {E}} \\[ 5pt ] \end{eqnarray}
\] となり，③式に該当する。

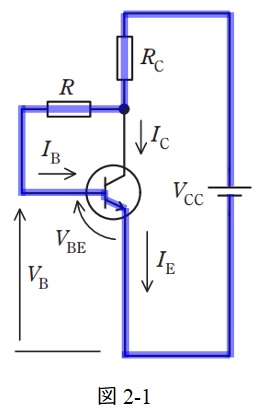
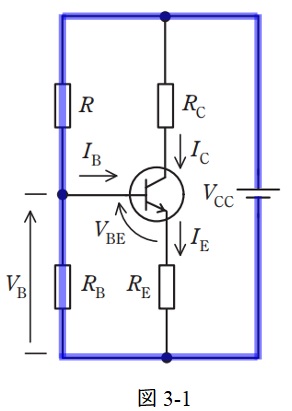
図3-1に示す閉回路において，ベース電流\( \ I_{\mathrm {B}} \ \)は十分に小さいとすると，ベース電位\( \ V_{\mathrm {B}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {B}}&=&\frac {R_{\mathrm {B}}}{R+R_{\mathrm {B}}}V_{\mathrm {CC}}\\[ 5pt ] \end{eqnarray}
\] となり，ほぼ一定となる。これより，エミッタ電流\( \ I_{\mathrm {E}} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {E}}&=&\frac {V_{\mathrm {B}}-V_{\mathrm {BE}}}{R_{\mathrm {E}}} \\[ 5pt ] \end{eqnarray}
\] となり，上式を変形すると，
\[
\begin{eqnarray}
R_{\mathrm {E}}I_{\mathrm {E}}&=&V_{\mathrm {B}}-V_{\mathrm {BE}} \\[ 5pt ] V_{\mathrm {BE}}&=&V_{\mathrm {B}}-R_{\mathrm {E}}I_{\mathrm {E}} \\[ 5pt ] \end{eqnarray}
\] となり，①式に該当する。