【問題】
【難易度】★★★★☆（やや難しい）
いろいろな変圧器に関する記述として，誤っているものを次の(1)～(5)のうちから一つ選べ。
(1) 単巻変圧器は，一つの巻線の一部から端子が出ており，巻線の共通部分を分路巻線，共通でない部分を直列巻線という。三相結線にして電力系統の電圧変成などに用いられる。
(2) 単相変圧器\( \ 3 \ \)台を\( \ \Delta – \Delta \ \)結線として三相給電しているとき，故障等により\( \ 1 \ \)台を取り除いて残りの\( \ 2 \ \)台で同じ電圧のまま給電する方式を\( \ \mathrm {V} \ \)結線方式という。\( \ \mathrm {V} \ \)結線にすると変圧器の利用率はおよそ\( \ 0.866 \ \)倍に減少する。
(3) スコット結線変圧器は，\( \ \mathrm {M} \ \)変圧器，\( \ \mathrm {T} \ \)変圧器と呼ばれる単相変圧器\( \ 2 \ \)台を用いる。\( \ \mathrm {M} \ \)変圧器の中央タップに片端子を接続した\( \ \mathrm {T} \ \)変圧器の途中の端子と\( \ \mathrm {M} \ \)変圧器の両端の端子を三相電源の一次側入力端子とする。二次側端子からは位相差\( \ 180 \ \)度の二つの単相電源が得られる。この変圧器は，電気鉄道の給電などに用いられる。
(4) 計器用変成器は，送配電系統等の高電圧・大電流を低電圧・小電流に変成して指示計器にて計測するためなどに用いられる。このうち，計器用変圧器は，変圧比が\( \ 1 \ \)より大きく，定格二次電圧は一般に，\( \ 110 \ \mathrm {V} \ \)又は\( \ \displaystyle \frac {110}{\sqrt {3}} \ \mathrm {V} \ \)に統一されている。
(5) 計器用変成器のうち，変流器は，一次巻線の巻数が少なく，\( \ 1 \ \)本の導体を鉄心に貫通させた貫通形と呼ばれるものがある。二次側を開放したままで一次電流を流すと一次電流が全て励磁電流となり，二次端子には高電圧が発生するので，電流計を接続するなど短絡状態で使用する必要がある。
【ワンポイント解説】
単巻変圧器，\( \ \mathrm {V} \ \)結線，スコット結線，計器用変成器とやや受験生が戸惑う内容をすべて取り入れた問題です。
間違いがパッと見つかれば良いですが，各選択肢の文章が長く誤りが見つけにくい点等，問題としてはかなり難問の部類に入るかなという印象なので，本番で出題されたら一旦飛ばして後からじっくりと見返すのが良いかなと思います。
1.単相単巻変圧器
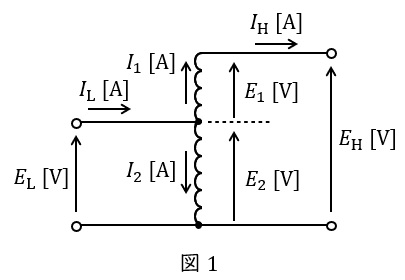
高圧側と低圧側の巻線の一部を共用する変圧器です。共用しない巻線を直列巻線(図1の\( \ E_{1} \ \)に当たる巻線)，共用する巻線を分路巻線(図1の\( \ E_{2} \ \)に当たる巻線)と言います。それぞれの電圧を図1のように定義し，自己容量を\( \ P_{1} \ \)，分路容量を\( \ P_{2} \ \)，線路容量を\( \ P_{3} \ \)とすると，
\[
\begin{eqnarray}
P_{1} &=&E_{1}I_{1} \\[ 5pt ]
&=&\left( E_{\mathrm {H}}-E_{\mathrm {L}}\right) I_{\mathrm {H}} \\[ 5pt ]
P_{2} &=&E_{2}I_{2} \\[ 5pt ]
&=&E_{\mathrm {L}}\left( I_{\mathrm {L}}-I_{\mathrm {H}}\right) \\[ 5pt ]
P_{3} &=&E_{\mathrm {H}}I_{\mathrm {H}} \\[ 5pt ]
&=&E_{\mathrm {L}}I_{\mathrm {L}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.\( \ \mathrm {\Delta -\Delta } \ \)結線と\( \ \mathrm {V-V} \ \)結線の比較
①\( \ \mathrm {\Delta -\Delta } \ \)結線
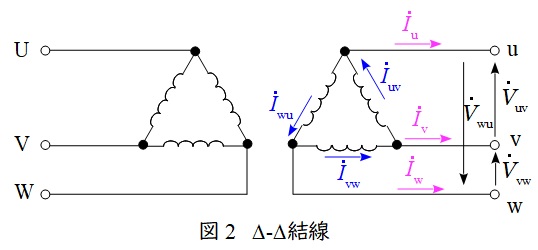
\( \ \mathrm {\Delta -\Delta } \ \)結線の変圧器の回路図とベクトル図を図2及び図3に示します。
図2において，負荷電流\( \ {\dot I}_{\mathrm {u}} \ \mathrm {[A]} \ \)は，変圧器を流れる電流\( \ {\dot I}_{\mathrm {uv}} \ \mathrm {[A]} \ \)及び\( \ {\dot I}_{\mathrm {wu}} \ \mathrm {[A]} \ \)を用いて，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {u}}&=& {\dot I}_{\mathrm {uv}}-{\dot I}_{\mathrm {wu}} \\[ 5pt ]
\end{eqnarray}
\]
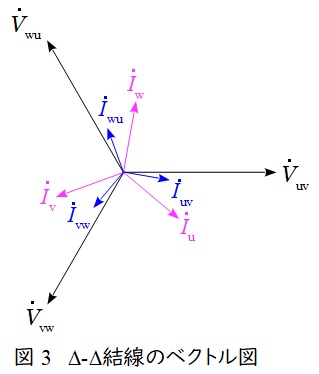
で求められ，ベクトル図上では図3のような関係となり，三相平衡である場合にはそれぞれの大きさの比は，
\[
\begin{eqnarray}
I_{\mathrm {u}}&=& \sqrt {3}I_{\mathrm {uv}} \\[ 5pt ]
\end{eqnarray}
\]
であることが分かります。したがって，各変圧器が分担する容量\( \ S \ \mathrm {[V\cdot A]} \ \)は，負荷の線間電圧を\( \ V_{\mathrm {uv}}=V_{\mathrm {vw}}=V_{\mathrm {wu}}=V \ \)，負荷電流を\( \ I_{\mathrm {u}}=I_{\mathrm {v}}=I_{\mathrm {w}}=I \ \)とすると，
\[
\begin{eqnarray}
S&=& \frac {VI}{\sqrt {3}} \\[ 5pt ]
\end{eqnarray}
\]
となります。したがって，変圧器全体の送電電力\( \ P \ \mathrm {[W]} \ \)は力率を\( \ \cos \theta \ \)とすると，
\[
\begin{eqnarray}
P&=& 3S\cos \theta \\[ 5pt ]
&=& 3\cdot \frac {VI}{\sqrt {3}}\cdot \cos \theta \\[ 5pt ]
&=&\sqrt {3}VI \cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となります。
②\( \ \mathrm {V -V } \ \)結線
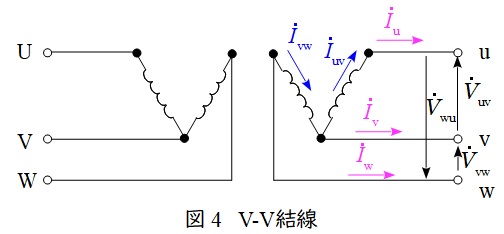
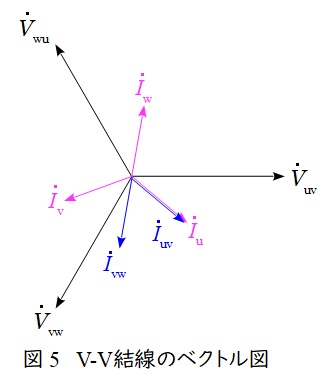
\( \ \mathrm {V -V } \ \)結線の変圧器の回路図とベクトル図を図4及び図5に示します。
図4において，負荷電流\( \ {\dot I}_{\mathrm {u}} \ \mathrm {[A]} \ \)，\( \ {\dot I}_{\mathrm {v}} \ \mathrm {[A]} \ \)，\( \ {\dot I}_{\mathrm {w}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {u}}&=& {\dot I}_{\mathrm {uv}} \\[ 5pt ]
{\dot I}_{\mathrm {v}}&=& {\dot I}_{\mathrm {vw}}-{\dot I}_{\mathrm {uv}} \\[ 5pt ]
{\dot I}_{\mathrm {w}}&=& -{\dot I}_{\mathrm {vw}} \\[ 5pt ]
\end{eqnarray}
\]
で求められ，ベクトル図上では図5のような関係となり，三相平衡である場合にはそれぞれの大きさの比は，
\[
\begin{eqnarray}
I_{\mathrm {u}}&=&I_{\mathrm {v}}&=&I_{\mathrm {w}}&=&I_{\mathrm {uv}}&=&I_{\mathrm {vw}} \\[ 5pt ]
\end{eqnarray}
\]
であることが分かります。したがって，各変圧器が分担する容量\( \ S \ \mathrm {[V\cdot A]} \ \)は，負荷の線間電圧を\( \ V_{\mathrm {uv}}=V_{\mathrm {vw}}=V_{\mathrm {wu}}=V \ \)，負荷電流を\( \ I_{\mathrm {u}}=I_{\mathrm {v}}=I_{\mathrm {w}}=I \ \)とすると，
\[
\begin{eqnarray}
S&=& VI \\[ 5pt ]
\end{eqnarray}
\]
となります。変圧器全体の送電電力\( \ P_{\mathrm {V}} \ \mathrm {[W]} \ \)は力率を\( \ \cos \theta \ \)とすると，
\[
\begin{eqnarray}
P_{\mathrm {V}}&=& \sqrt {3}VI \cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となるので，\( \ \mathrm {V -V } \ \)結線で得られる出力\( \ \mathrm {[V\cdot A]} \ \)は各変圧器の出力の\( \ \sqrt {3} \ \)倍となるため，利用率は，
\[
\begin{eqnarray}
利用率&=& \frac {\sqrt {3}VI}{2VI} \\[ 5pt ]
&=& \frac {\sqrt {3}}{2} → 86.6 \ \mathrm {[％]} \\[ 5pt ]
\end{eqnarray}
\]
となります。また，\( \ \mathrm {V -V } \ \)結線と\( \ \mathrm {\Delta -\Delta } \ \)結線で同じ電力を出力する場合に必要となる変圧器の容量比は，
\[
\begin{eqnarray}
容量比&=& \frac {\displaystyle \frac {VI}{\sqrt {3}}}{VI} \\[ 5pt ]
&=& \frac {1}{\sqrt {3}} → 57.7 \ \mathrm {[％]} \\[ 5pt ]
\end{eqnarray}
\]
となるため，\( \ \mathrm {V -V } \ \)結線の出力は\( \ \mathrm {\Delta -\Delta } \ \)結線の\( \ 57.7 \ \mathrm {[％]} \ \)程度であることがわかります。
3.スコット結線変圧器
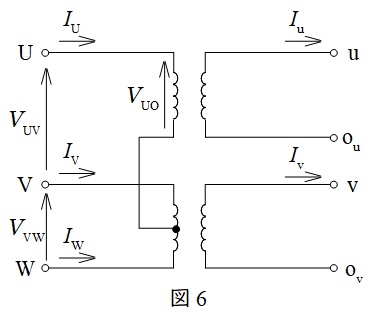
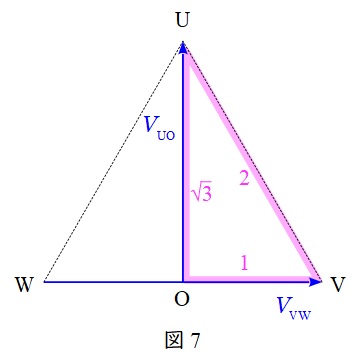
単相変圧器を図6のように接続することで，図7に示すようなベクトル図の電圧を取り出すことができる結線方式です。
一次側の\( \ V_{\mathrm {VW}} \ \)と\( \ V_{\mathrm {UO}} \ \)がそれぞれ二次側に変圧され，その電圧の大きさは図7に示す直角三角形の関係を用いれば\( \ 2 : \sqrt {3} \ \)であることが分かります。
したがって，巻数比の関係を\( \ 2 : \sqrt {3} \ \)とすれば，二次側に同じ大きさで位相が\( \ 90° \ \)異なる電圧を取り出すことができます。
4.計器用変成器
計器用変成器はそのままでは測定困難な高電圧や大電流を測定可能な大きさの電圧や電流に変成して測定機器を接続する機器です。計器用変圧器と変流器があります。
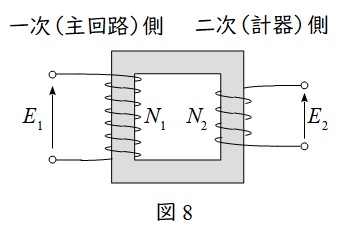
①計器用変圧器\( \ \left( \mathrm {VT} \right) \ \)
図8のように一次（主回路）側の高電圧を二次（計器）側の低電圧に変換する機器となります。
一次二次の巻数比と変圧比の関係は，
\[
\begin{eqnarray}
\frac {N_{1}}{N_{2}}&=&\frac {V_{1}}{V_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
計器用変圧器\( \ \mathrm {VT} \ \)の二次側を短絡すると，二次側に電圧を発生させるため過大な電流が流れ，機器の焼損や波及事故が発生してしまう可能性があるので，二次側は絶対に短絡してはいけません。
②変流器\( \ \left( \mathrm {CT} \right) \ \)
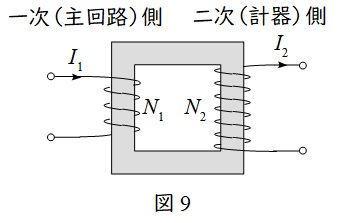
図9のように一次（主回路）側の大電流を二次（計器）側の測定電流に変換する機器となります。
一次二次の巻数比と変流比の関係は，
\[
\begin{eqnarray}
\frac {N_{1}}{N_{2}}&=&\frac {I_{2}}{I_{1}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
変流器\( \ \mathrm {CT} \ \)の二次側を開放すると測定電流が全て励磁電流となるので，鉄心の磁束密度が著しく大きくなり，焼損するおそれがあります。したがって，二次側は絶対に開放してはいけません。
【解答】
解答：(3)
(1)：正しい
ワンポイント解説「1.単相単巻変圧器」の通り，一つの巻線の一部から端子が出ており，巻線の共通部分を分路巻線，共通でない部分を直列巻線といいます。
(2)：正しい
ワンポイント解説「2.\( \ \mathrm {\Delta -\Delta } \ \)結線と\( \ \mathrm {V-V} \ \)結線の比較」の通りです。\( \ \mathrm {V} \ \)結線にすると変圧器の利用率はおよそ\( \ 0.866 \ \)倍に減少します。
(3)：誤り
ワンポイント解説「3.スコット結線変圧器」の通り，スコット結線変圧器は，\( \ \mathrm {M} \ \)変圧器，\( \ \mathrm {T} \ \)変圧器と呼ばれる単相変圧器\( \ 2 \ \)台を用い，\( \ \mathrm {M} \ \)変圧器の中央タップに片端子を接続した\( \ \mathrm {T} \ \)変圧器の途中の端子と\( \ \mathrm {M} \ \)変圧器の両端の端子を三相電源の一次側入力端子とします。そして，二次側端子からは二つの単相電源が得られますが位相差は\( \ 90 \ \)度となります。
(4)：正しい
ワンポイント解説「4.計器用変成器」の通り，計器用変成器は，送配電系統等の高電圧・大電流を低電圧・小電流に変成して指示計器にて計測するためなどに用いられます。計器用変圧器は，変圧比が\( \ 1 \ \)より大きく，定格二次電圧は一般に\( \ 110 \ \mathrm {V} \ \)又は\( \ \displaystyle \frac {110}{\sqrt {3}} \ \mathrm {V} \ \)です。
(5)：正しい
ワンポイント解説「4.計器用変成器」の通り，変流器は，一次巻線の巻数が少なく，\( \ 1 \ \)本の導体を鉄心に貫通させた貫通形と呼ばれるものがあります。二次側を開放したままで一次電流を流すと一次電流が全て励磁電流となり，二次端子には高電圧が発生するので，電流計を接続するなど短絡状態で使用する必要があります。
愛知県出身 愛称たけちゃん
詳しくは