《理論》〈電気及び電子計測〉[H22:問16]電力量計の原理と誤差率に関する空欄穴埋及び計算問題

【問題】

【難易度】★★★★☆（やや難しい）

電力量計について，次の(a)及び(b)に答えよ。

(a)　次の文章は，交流の電力量計の原理について述べたものである。

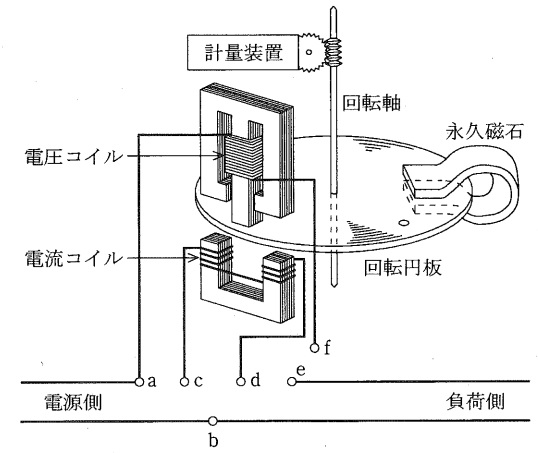
計器の指針等を駆動するトルクを発生する動作原理により計器を分類すると，図に示した構造の電力量計の場合は，\( \ \fbox {　 （ア） 　} \ \)に分類される。

この計器の回転円板が負荷の電力に比例するトルクで回転するように，図中の端子\( \ \mathrm {a} \ \)から\( \ \mathrm {f} \ \)を\( \ \fbox {　 （イ） 　} \ \)のように接続して，負荷電圧を電圧コイルに加え，負荷電流を電流コイルに流す。 その結果，コイルに生じる磁束による移動磁界と，回転円板上に生じる渦電流との電磁力の作用で回転円板は回転する。

一方，永久磁石により回転円板には速度に比例する\( \ \fbox {　 （ウ） 　} \ \)が生じ，負荷の電力に比例する速度で回転円板は回転を続ける。したがって，計量装置でその回転数をある時間計量すると，その値は同時間中に消費された電力量を表す。

上記の記述中の空白箇所(ア)，(イ)及び(ウ)に当てはまる語句又は記号として，正しいものを組み合わせたのは次のうちどれか。

\[
\begin{array}{cccc}
& （ア） & （イ） & （ウ） \\
\hline
(1) & 　誘導形　　　 & 　\mathrm {ac,de,bf}　 & 　駆動トルク　 \\
\hline
(2) & 　電流力計形　 & 　\mathrm {ad,bc,ef}　 & 　制動トルク　 \\
\hline
(3) & 　誘導形　　　 & 　\mathrm {ac,de,bf}　 & 　制動トルク　 \\
\hline
(4) & 　電流力計形　 & 　\mathrm {ad,bc,ef}　 & 　駆動トルク　 \\
\hline
(5) & 　電力計形　　 & 　\mathrm {ac,de,bf}　 & 　駆動トルク　 \\
\hline
\end{array}
\]

(b)　上記(a)の原理の電力量計の使用の可否を検討するために，電力量計の計量の誤差率を求める実験を行った。 実験では，\( \ 3 \ \mathrm {[kW]} \ \)の電力を消費している抵抗負荷の交流回路に，この電力量計を接続した。 このとき，電力量計はこの抵抗負荷の消費電力量を計量しているので，計器の回転円板の回転数を測定することから計量の誤差率を計算できる。

電力量計の回転円板の回転数を測定したところ，回転数は\( \ 1 \ \)分間に\( \ 61 \ \)であった。この場合，電力量計の計量の誤差率\( \ \mathrm {[％]} \ \)の大きさの値として最も近いのは次のうちどれか。

ただし，電力量計の計器定数(\( \ 1 \ \mathrm {[kW\cdot h]} \ \)当たりの回転円板の回転数)は，\( \ 1 \ 200 \ \mathrm {[rev / kW\cdot h]} \ \)であり，回転円板の回転数と計量装置の計量値の関係は正しいものとし，電力損失は無視できるものとする。

　(1)　\( \ 0.2 \ \)　　(2)　\( \ 0.4 \ \)　　(3)　\( \ 1.0 \ \)　　(4)　\( \ 1.7 \ \)　　(5)　\( \ 2.1 \ \)

【ワンポイント解説】

電力量計の原理と誤差率の計算に関する問題です。
やや内容がマイナーであり，より現場に近い内容であることから，受験生には少し厳しい問題であったかもしれません。

1.誘導形計器
アラゴの円板の原理を利用した計器です。
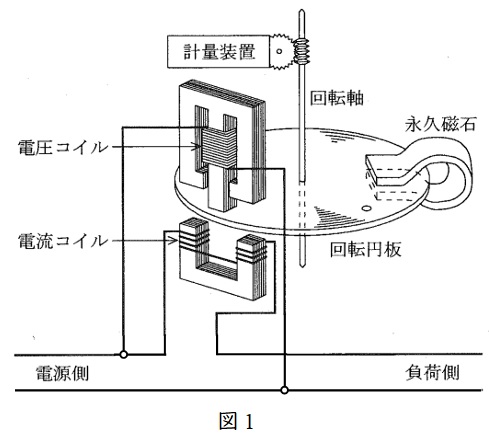
図1に示すように電流コイルを発生する磁束が逆向きになるように巻き，電圧コイルにはインダクタンスを大きくして電流コイルの各磁束に対して位相が\( \ 90° \ \)異なる磁束を発生させ，全体として移動磁界を発生させます。これにより，有効電力に比例した回転力が回転円板に与えられます。
しかしながら，この状態では電力がなくなっても回転し続けてしまうので，制動磁石と呼ばれる逆向きの磁束を発生させる永久磁石を設け，これによって回転円板に制動トルクを働かせ，電力に比例した回転数で円板を回転させます。
計量装置は回転軸と歯車で接続し，その回転数によって電力量を計測します。

2.電流力計形計器
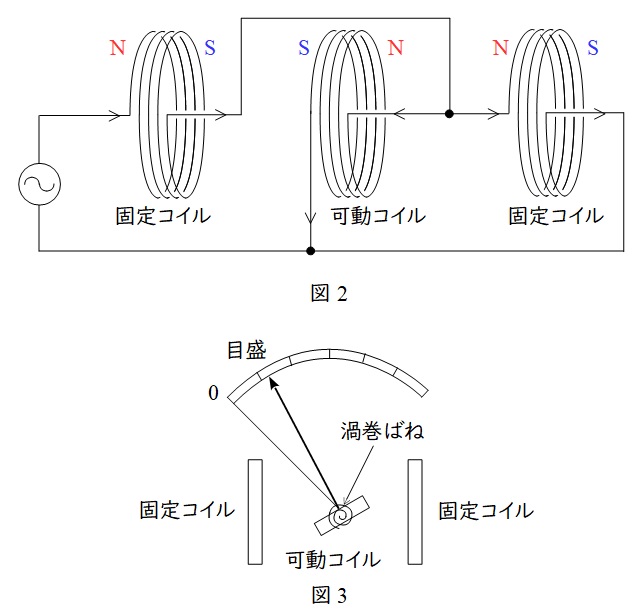
図2のように三つのコイルを配置し，中央のコイルを可動式にし，両端のコイルを固定式にします。
それぞれのコイルには右ねじの法則により磁界が発生し磁化されますが，可動コイルだけ電流を逆向きに流すことにより，それぞれに反発力が生まれます。
反発力の大きさが測定する電流の大きさに比例するので，図3のように可動コイルに指針をつけ軸で回転させることにより，電流の大きさや負荷電力の大きさを測定することが可能となります。また，電流がなくなった場合に元の位置に戻るように渦巻ばねが設けられています。
逆向きに流れてもすべての\( \ \mathrm {N} \ \)極と\( \ \mathrm {S} \ \)極が反転し同様の反発力が発生するため，直流・交流ともに測定可能となります。

3.誤差及び誤差率の定義
真値を\( \ T \ \)，測定値を\( \ M \ \)とすると，誤差\( \ \varepsilon \ \)と誤差率\( \ ％\varepsilon \ \)は，
\[
\begin{eqnarray}
\varepsilon &=&M-T \\[ 5pt ] ％\varepsilon &=&\frac {M-T}{T} \times 100 \ [％] \end{eqnarray}
\] となります。

【解答】

(a)解答：(3)
(ア)
ワンポイント解説「1.誘導形計器」の通り，問題図の電力量計は誘導形となります。

(イ)
ワンポイント解説「1.誘導形計器」図1の通り，電圧コイルには負荷の電圧が加わるように並列に，電流コイルには負荷電流が流れるように直列に接続します。したがって，\( \ \mathrm {ac,de,bf} \ \)と接続します。

(ウ)
ワンポイント解説「1.誘導形計器」の通り，永久磁石により発生させるのは制動トルクとなります。

(b)解答：(4)
題意より，電力量計の計器定数(\( \ 1 \ \mathrm {[kW\cdot h]} \ \)当たりの回転円板の回転数)は\( \ 1 \ 200 \ \mathrm {[rev / kW\cdot h]} \ \)であるから，\( \ 3 \ \mathrm {[kW]} \ \)で\( \ 1 \ \)時間運転したときの回転数すなわち真値\( \ T \ \)は，
\[
\begin{eqnarray}
T &=&3\times 1200 \\[ 5pt ] &=&3 \ 600 \ \mathrm {[rev]} \\[ 5pt ] \end{eqnarray}
\] となる。一方，\( \ 1 \ \)時間当たりの測定値\( \ M \ \)は，回転数が\( \ 1 \ \)分間に\( \ 61 \ \)であることから，
\[
\begin{eqnarray}
M &=&60\times 61 \\[ 5pt ] &=&3 \ 660 \ \mathrm {[rev]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，誤差率\( \ ％\varepsilon \ \mathrm {[％]} \ \)は，ワンポイント解説「3.誤差及び誤差率の定義」より，
\[
\begin{eqnarray}
％\varepsilon &=&\frac {M-T}{T} \times 100 \\[ 5pt ] &=&\frac {3 \ 660-3 \ 600}{3 \ 600} \times 100 \\[ 5pt ] &≒&1.7 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。