Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
無限に長い直線状導体に直流電流を流すと,導体の周りに磁界が生じる。この磁界中に小磁針を置くと,小磁針の\( \ \fbox { (ア) } \ \)は磁界の向きを指して静止する。そこで,小磁針を磁界の向きに沿って少しずつ動かしていくと,導体を中心とした\( \ \fbox { (イ) } \ \)の線が得られる。この線に沿って磁界の向きに矢印をつけたものを\( \ \fbox { (ウ) } \ \)という。
また,磁界の強さを調べてみると,電流の大きさに比例し,導体からの\( \ \fbox { (エ) } \ \)に反比例している。
上記の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & \mathrm {N} \ 極 & 放射状 & 電気力線 & 距離の \ 2 \ 乗 \\
\hline
(2) & \mathrm {N} \ 極 & 同心円状 & 電気力線 & 距離の \ 2 \ 乗 \\
\hline
(3) & \mathrm {S} \ 極 & 放射状 & 磁力線 & 距離 \\
\hline
(4) & \mathrm {N} \ 極 & 同心円状 & 磁力線 & 距離 \\
\hline
(5) & \mathrm {S} \ 極 & 同心円状 & 磁力線 & 距離の \ 2 \ 乗 \\
\hline
\end{array}
\]
【ワンポイント解説】
直線状導体が作る磁界に関する問題です。
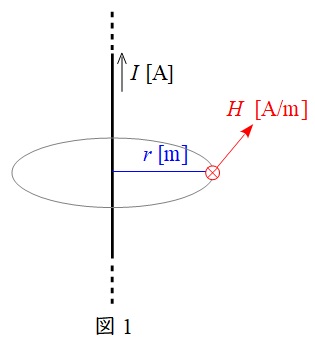
図が与えられていないので図1に示すような図を簡単に描くと良いかと思います。
電界→電気力線,磁界→磁力線と名称も特徴も似ていますが,電気と磁気の違いをしっかりと理解しておきましょう。
1.アンペールの周回積分の法則
図1のように無限長直線電流\( \ I \ \mathrm {[A]} \ \)が流れているとき,電線から距離\( \ r \ \mathrm {[m]} \ \)離れた位置での磁界の強さ\( \ H \ \mathrm {[A / m]} \ \)は,
\[
\begin{eqnarray}
H&=&\frac {I}{2\pi r} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
2.磁力線の特徴
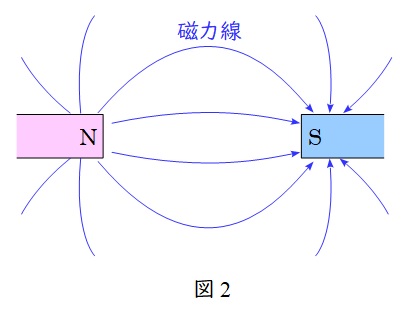
磁力線は\( \ \mathrm {N} \ \)極から出て\( \ \mathrm {S} \ \)極に向かう仮想の線で,以下のような特徴があります。
①磁力線の本数は磁荷\( \ m \ \mathrm {[Wb]} \ \),透磁率\( \ \mu \ \mathrm {[H/m]} \ \)を用いると,\( \ \displaystyle \frac {m}{\mu } \ \)本である。
②磁力線は\( \ \mathrm {N} \ \)極から出て\( \ \mathrm {S} \ \)極に入る。
③磁力線同士は反発し合う。
④磁力線は枝分かれしたり,交差したりしない。
⑤磁力線の向きは磁界の向きと一致し,磁力線の密度は磁界の強さに比例する。
【解答】
解答:(4)
(ア)
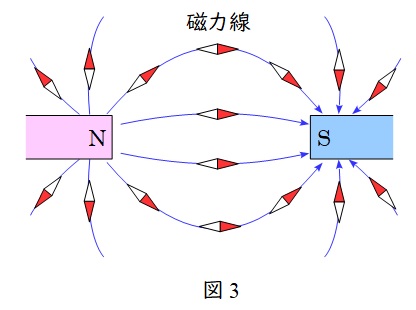
小磁針の\( \ \mathrm {N} \ \)極が\( \ \mathrm {S} \ \)極と引き合うので,図3に示すように任意の位置において磁界の向き(磁力線の向き)と\( \ \mathrm {N} \ \)極の向きは等しくなります。
(イ)
ワンポイント解説「1.アンペールの周回積分の法則」の通り,磁界の向きは円方向の向きとなるので,小磁針を磁界の向きに沿って少しずつ動かしていくと,導体を中心とした同心円状の線が描けます。
(ウ)
ワンポイント解説「2.磁力線の特徴」の通り,磁界の向きに矢印をつけたものを磁力線といいます。
(エ)
ワンポイント解説「1.アンペールの周回積分の法則」の通り,磁界の強さ\( \ H \ \mathrm {[A / m]} \ \)は,電流の大きさ\( \ I \ \mathrm {[A]} \ \),導体からの距離\( \ r \ \mathrm {[m]} \ \)とすると,
\[
\begin{eqnarray}
H&=&\frac {I}{2\pi r} \\[ 5pt ]
\end{eqnarray}
\]
で求められ,電流の大きさ\( \ I \ \mathrm {[A]} \ \)に比例し,導体からの距離\( \ r \ \mathrm {[m]} \ \)に反比例します。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは