《理論》〈電気回路〉[H21:問16]三相平衡回路の線電流と相電流の導出に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

平衡三相回路について，次の(a)及び(b)に答えよ。

(a)　図1のように，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)が接続された平衡三相負荷に線間電圧\( \ E \ \mathrm {[V]} \ \)の対称三相交流電源を接続した。このとき，図1に示す電流\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)の大きさの値を表す式として，正しいのは次のうちどれか。

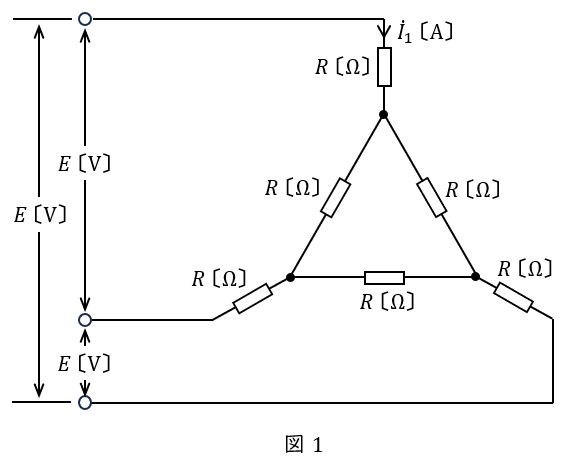
　(1)　\( \ \displaystyle \frac {E}{4\sqrt {3}R} \ \)　　(2)　\( \ \displaystyle \frac {E}{4R} \ \)　　(3)　\( \ \displaystyle \frac {\sqrt {3}E}{4R} \ \)　　(4)　\( \ \displaystyle \frac {\sqrt {3}E}{R} \ \)　　(5)　\( \ \displaystyle \frac {4E}{\sqrt {3}R} \ \)

(b)　次に，図1を図2のように，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)をインピーダンス\( \ \dot Z=12+\mathrm {j}9 \ \mathrm {[\Omega ]} \ \)の負荷に置き換え，線間電圧\( \ E=200 \ \mathrm {[V]} \ \)とした。このとき，図2に示す電流\( \ {\dot I}_{2} \ \mathrm {[A]} \ \)の大きさの値として，最も近いのは次のうちどれか。

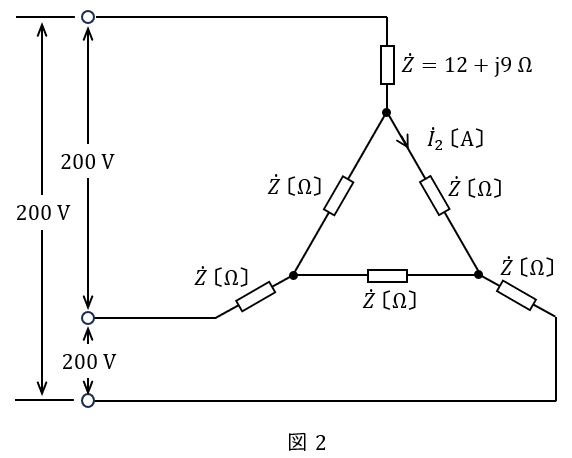
　(1)　\( \ 2.5 \ \)　　(2)　\( \ 3.3 \ \)　　(3)　\( \ 4.4 \ \)　　(4)　\( \ 5.8 \ \)　　(5)　\( \ 7.7 \ \)

【ワンポイント解説】

三相平衡回路の線電流と相電流の導出に関する問題です。
\( \ \Delta -\mathrm {Y} \ \)変換を使用する等の解法は比較的イメージつくかと思いますが，相電圧と線間電圧，線電流と相電流の関係に迷う受験生が多かったかと思います。

1.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換
①\( \ \Delta -\mathrm {Y} \ \)変換
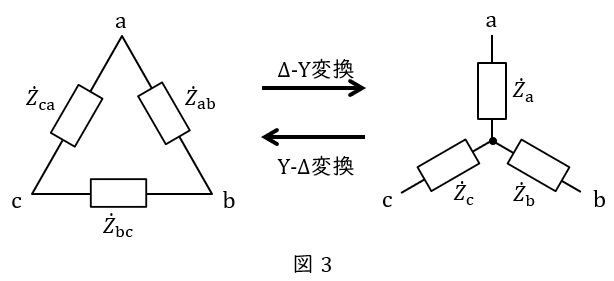
図3において，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}}&=&\frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] {\dot Z}_{\mathrm {b}}&=&\frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] {\dot Z}_{\mathrm {c}}&=&\frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] \end{eqnarray}
\] ②\( \ \mathrm {Y}-\Delta \ \)変換
図3において，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ] {\dot Z}_{\mathrm {bc}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ] {\dot Z}_{\mathrm {ca}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ] \end{eqnarray}
\] 平衡三相回路においては，
\[
{\dot Z}_{\mathrm {ab}}={\dot Z}_{\mathrm {bc}}={\dot Z}_{\mathrm {ca}}=3{\dot Z}_{\mathrm {a}}=3{\dot Z}_{\mathrm {b}}=3{\dot Z}_{\mathrm {c}}
\] となります。

2.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係
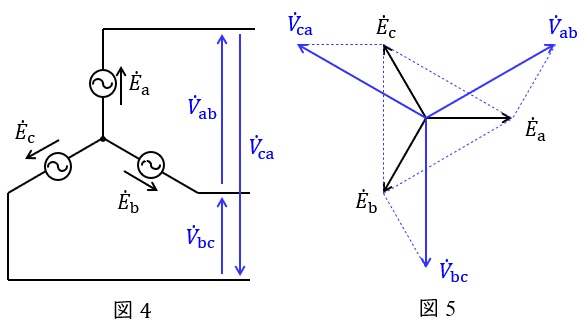
図4のような三相対称電源がある時，線間電圧と相電圧の関係は図5のベクトル図のようになり，線間電圧の大きさ\( \ V \ \)は相電圧の大きさ\( \ E \ \)と比較すると，
\[
\begin{eqnarray}
V_{\mathrm {ab}} &=&\sqrt {3}E_{\mathrm {a}} \\[ 5pt ] V_{\mathrm {bc}} &=&\sqrt {3}E_{\mathrm {b}} \\[ 5pt ] V_{\mathrm {ca}} &=&\sqrt {3}E_{\mathrm {c}} \\[ 5pt ] \end{eqnarray}
\] かつ\( \ \displaystyle \frac {\pi }{6} \)（30°)進みであることが分かります。

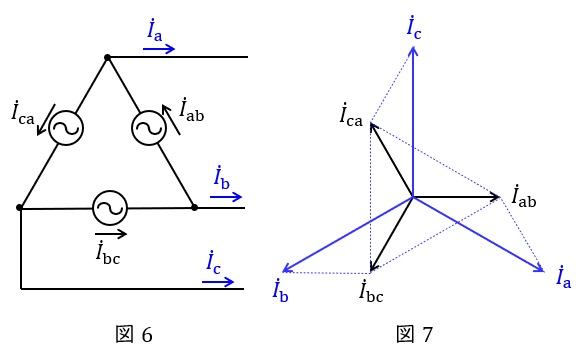
3.\( \ \Delta \ \)結線における相電流と線電流の関係
図6のような三相対称電源がある時，線電流と相電流の関係は図7のベクトル図のようになり，線電流の大きさは相電流の大きさと比較すると，
\[
\begin{eqnarray}
I_{\mathrm {a}} &=&\sqrt {3}I_{\mathrm {ab}} \\[ 5pt ] I_{\mathrm {b}} &=&\sqrt {3}I_{\mathrm {bc}} \\[ 5pt ] I_{\mathrm {c}} &=&\sqrt {3}I_{\mathrm {ca}} \\[ 5pt ] \end{eqnarray}
\] かつ\( \ \displaystyle \frac {\pi }{6} \)（30°)遅れであることが分かります。

【解答】

(a)解答：(3)
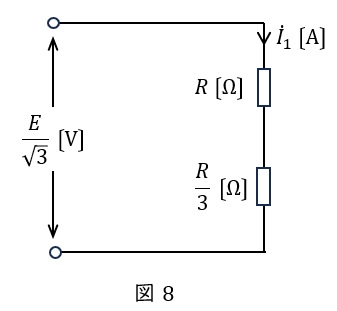
図1の\( \ \Delta \ \)結線の各抵抗を\( \ \Delta -\mathrm {Y} \ \)変換すると，ワンポイント解説「1.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換」の通り，三相平衡回路であるから\( \ \displaystyle \frac {R}{3} \ \mathrm {[\Omega ]} \ \)となる。
したがって，一相分等価回路は図8のようになるので，電流\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)の大きさ\( \ I_{1} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{1} &=&\frac {\displaystyle \frac {E}{\sqrt {3}}}{\displaystyle R+\frac {R}{3}} \\[ 5pt ] &=&\frac {\displaystyle \frac {E}{\sqrt {3}}}{\displaystyle \frac {4R}{3}} \\[ 5pt ] &=&\frac {3E}{4\sqrt {3}R} \\[ 5pt ] &=&\frac {\sqrt {3}E}{4R} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(2)
(a)解答より，図2の線電流の大きさ\( \ I_{2}^{\prime } \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{2}^{\prime } &=&\frac {\sqrt {3}E}{4Z} \\[ 5pt ] &=&\frac {\sqrt {3}\times 200}{4\times \sqrt {12^{2}+9^{2}}} \\[ 5pt ] &=&\frac {\sqrt {3}\times 200}{4\times 15} \\[ 5pt ] &=&\frac {10\sqrt {3}}{3} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，ワンポイント解説「3.\( \ \Delta \ \)結線における相電流と線電流の関係」の通り，\( \ \Delta \ \)結線においては線電流は相電流の\( \ \sqrt {3} \ \)倍であるから，
\[
\begin{eqnarray}
I_{2} &=&\frac {I_{2}^{\prime }}{\sqrt {3}} \\[ 5pt ] &=&\frac {\displaystyle \frac {10\sqrt {3}}{3}}{\sqrt {3}}\\[ 5pt ] &=&\frac {10}{3} \\[ 5pt ] &≒&3.33 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。