《理論》〈電磁気〉[R05上:問10]コイルを接続した回路に現れる電圧の最大値に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

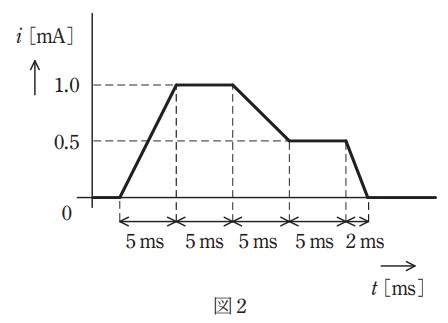
図1のように，インダクタンス$\ L＝5 \ \mathrm {H} \ $のコイルに直流電流源$\ J \ $が電流$\ i \ \mathrm {[mA]} \ $を供給している回路がある。電流$\ i \ \mathrm {[mA]} \ $は図2のような時間変化をしている。このとき，コイルの端子間に現れる電圧の大きさ$\ \left| v\right| \ $の最大値$\ \mathrm {[V]} \ $として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　$\ 0.25 \ $　　(2)　$\ 0.5 \ $　　(3)　$\ 1 \ $　　(4)　$\ 1.25 \ $　　(5)　$\ 1.5 \ $

【ワンポイント解説】

電流源とコイルを接続した回路のコイルに現れる電圧の導出に関する問題です。
電磁誘導の自己インダクタンスの公式を覚えていれば，比較的容易に解ける問題かと思います。
平成16年問9からの再出題の問題となります。

1.ファラデーの電磁誘導の法則と自己インダクタンス$\ L \ $
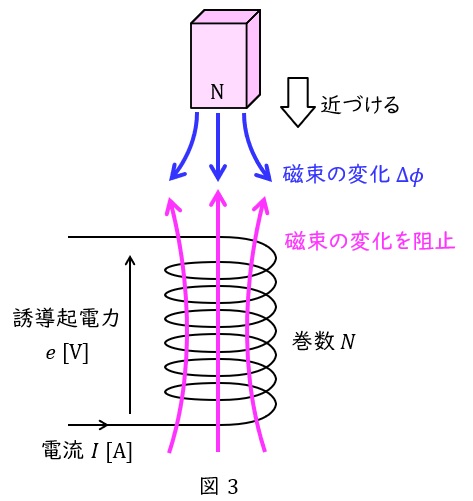
図3に示すように，巻数$\ N \ $のコイルを貫通する磁束$\ \phi \ \mathrm {[Wb]} \ $があるとき，ファラデーの電磁誘導の法則より，コイルに発生する誘導起電力$\ e \ \mathrm {[V]} \ $は，磁束の時間変化$\ \displaystyle \frac {\Delta \phi }{\Delta t} \ $に比例し，

$$\begin{eqnarray} e&=&−N\frac {\Delta \phi }{\Delta t} \\[ 5pt ] \end{eqnarray}$$ で求められます。これをファラデーの電磁誘導の法則といいます。一方，電流変化$\ \Delta I \ \mathrm {[A]} \ $を考える場合，
$$\begin{eqnarray} e&=&−L\frac {\Delta I }{\Delta t} \\[ 5pt ] \end{eqnarray}$$ という関係も成り立ち，$\ L \ \mathrm {[H]}\ $を自己インダクタンスと言います。これらの関係から，
$$\begin{eqnarray} −N\frac {\Delta \phi }{\Delta t}&=&−L\frac {\Delta I }{\Delta t} \\[ 5pt ] N\phi &=&LI \\[ 5pt ] \end{eqnarray}$$ の関係があります。

【解答】

解答：(4)
図2において最も電流変化が大きいのは最後の$\ \Delta t=2 \ \mathrm {[ms]} \ $で，$\ \Delta i=-0.5 \ \mathrm {[mA]} \ $の時である。したがって，このときのコイルの端子間に現れる電圧の大きさ$\ v \ \mathrm {[V]} \ $は，ワンポイント解説「1.ファラデーの電磁誘導の法則と自己インダクタンス$\ L \ $」の通り，

$$\begin{eqnarray} v&=&−L\frac {\Delta I }{\Delta t} \\[ 5pt ] &=&−5\times \frac {-0.5\times 10^{-3}}{2\times 10^{-3}} \\[ 5pt ] &=&1.25 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}$$ と求められる。