《法規》〈電気設備技術基準〉[H28:問12]高圧ケーブルの交流絶縁耐力試験に関する計算問題

【問題】

【難易度】★★★★★（難しい）

「電気設備技術基準の解釈」に基づいて，使用電圧\( \ \mathrm {6600 \ V} \ \)，周波数\( \ \mathrm {50 \ Hz} \ \)の電路に接続する高圧ケーブルの交流絶縁耐力試験を実施する。次の(a)及び(b)の問に答えよ。
ただし，試験回路は図のとおりとする。高圧ケーブルは\( \ 3 \ \)線一括で試験電圧を印加するものとし，各試験機器の損失は無視する。また，被試験体の高圧ケーブルと試験用変圧器の仕様は次のとおりとする。

【高圧ケーブルの仕様】
ケーブルの種類：\( \ \mathrm {6 \ 600 \ V} \ \)トリプレックス形架橋ポリエチレン絶縁ビニルシースケーブル(\( \ \mathrm {CVT} \ \))
公称断面積：\( \ \mathrm {100 \ mm^{2}} \ \)，ケーブルのこう長：\( \ \mathrm {87 \ m} \ \)
1線の対地静電容量：\( \ \mathrm {0.45 \ \mu F / km} \ \)

【試験用変圧器の仕様】
定格入力電圧：\( \ \mathrm {AC } \ \)　\( \ \mathrm {0-120 \ V } \ \)，定格出力電圧：\( \ \mathrm {AC } \ \)　\( \ \mathrm {0-12 \ 000 \ V } \ \)
入力電源周波数：\(\mathrm {50Hz}\)

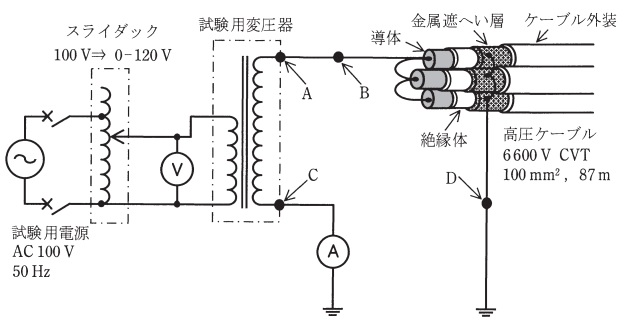
(a)　この交流絶縁耐力試験に必要な皮相電力(以下，試験容量という。)の値\( \ \mathrm { [ kV\cdot A ] } \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

(1)　\( \ 1.4 \ \)　　(2)　\( \ 3.0 \ \)　　(3)　\( \ 4.0 \ \)　　(4)　\( \ 4.8 \ \)　　(5)　\( \ 7.0 \ \)

(b)　上記(a)の計算の結果，試験容量が使用する試験用変圧器の容量よりも大きいことがわかった。そこで，この試験回路に高圧補償リアクトルを接続し，試験容量を試験用変圧器の容量より小さくすることができた。
このとき，同リアクトルの接続位置(図中の\( \ \mathrm {A～D} \ \)のうちの\( \ 2 \ \)点間)と，試験用変圧器の容量の値\( \ \mathrm { [ kV\cdot A ] } \ \)の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
ただし，接続する高圧補償リアクトルの仕様は次のとおりとし，接続する台数は1台とする。また，同リアクトルによる損失は無視し，\( \ \mathrm {A}\)-\(\mathrm {B} \ \)間に同リアクトルを接続する場合は，図中の\( \ \mathrm {A}\)-\(\mathrm {B} \ \)間の電線を取り除くものとする。

【高圧補償リアクトルの仕様】
定格容量：\( \ \mathrm {3.5 \ kvar } \ \)，定格周波数：\( \ \mathrm {50 \ Hz} \ \)，定格電圧：\( \ \mathrm {12 \ 000 \ V } \ \)
電流：\( \ \mathrm {292 \ mA } \ \) ( \( \ \mathrm {12 \ 000 \ V } \ \)　\( \ \mathrm {50 \ Hz } \ \)印加時)
\[
\begin{array}{ccc}
& 高圧補償リアクトル接続位置 & 試験用変圧器の容量 \ [\mathrm {kV\cdot A}] \\
\hline
(1) & \mathrm {A}－\mathrm {B} \ 間 & 1 \\
\hline
(2) & \mathrm {A}－\mathrm {C} \ 間 & 1 \\
\hline
(3) & \mathrm {C}－\mathrm {D} \ 間 & 2 \\
\hline
(4) & \mathrm {A}－\mathrm {C} \ 間 & 2 \\
\hline
(5) & \mathrm {A}－\mathrm {B} \ 間 & 3 \\
\hline
\end{array}
\]

【ワンポイント解説】

問題の難易度としては二種や一種の一次試験にも出ても良さそうな内容です。ただ最大使用電圧を暗記しているのみでは解けず，電力科目の知識も総合的に問われている良問と言えると思います。

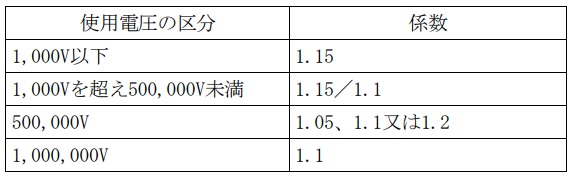
1.最大使用電圧
最大使用電圧は下表のとおりとなりますが，電験で出題されるのは係数\(\displaystyle \frac {1.15}{1.1}\)のみです。
＜電気設備技術基準の解釈第1条(抜粋)＞

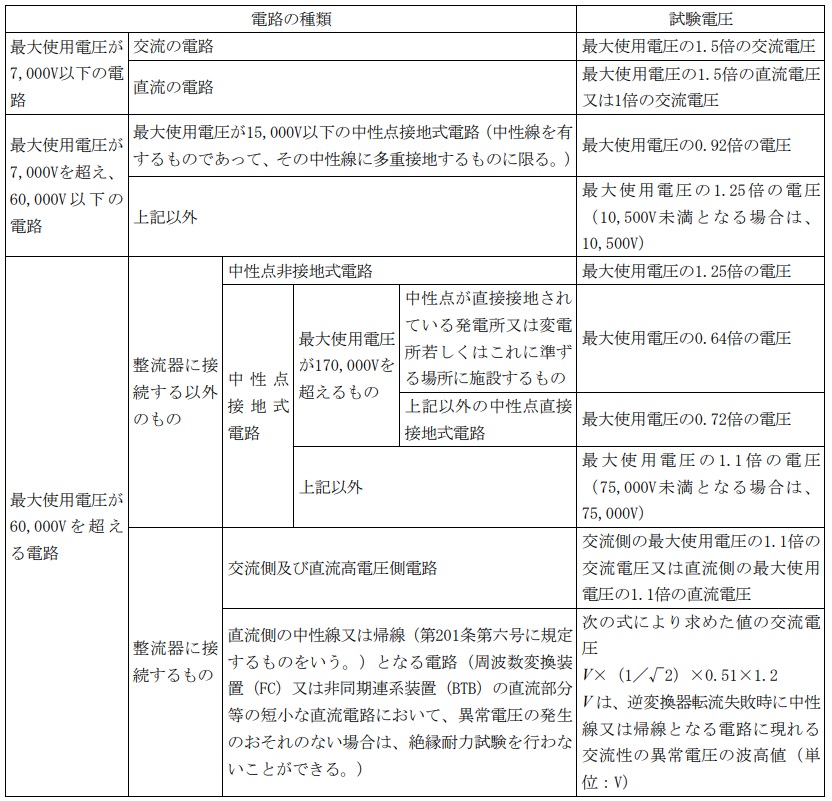
2.試験電圧
試験電圧は下表の通り細かく分かれています。最初に覚えておくべき内容は交流の試験電圧で，
　　\( \ 1.5 \ \times \ \)最大使用電圧　(最大使用電圧が\( \ 7 \ 000 \ \mathrm {V} \ \)以下の時)
　　\( \ 1.25 \ \times \ \)最大使用電圧　(最大使用電圧が\( \ 7 \ 000 \ \mathrm {V} \ \)を超え\( \ 60 \ 000 \ \mathrm {V} \ \)以下の時)
となります。

＜電気設備技術基準の解釈第15条(抜粋)＞

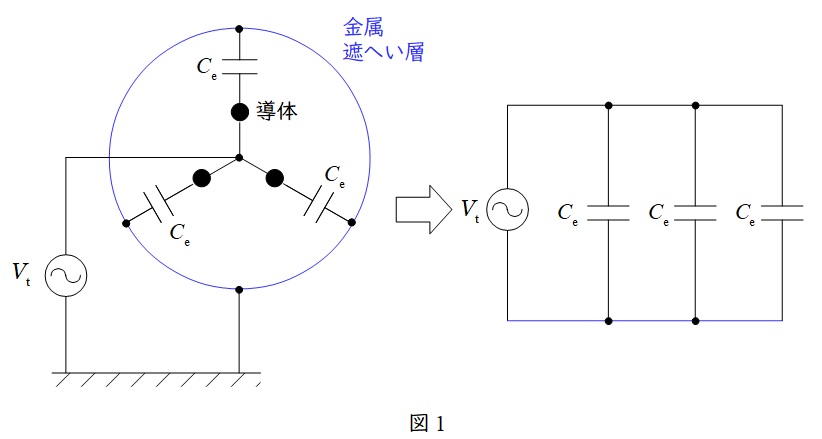
3.ケーブルの試験等価回路
\( \ \mathrm {CVT} \ \)ケーブルの断面図は下図のようになり，各相間および各祖と大地との間に静電容量を持ちます。\( \ 3 \ \)線一括の交流絶縁耐力試験では，各相間の静電容量は短絡されるので，静電容量は各相と金属遮へい層の間のみを考慮すればよく，金属遮へい層は接地されているので，等価回路は右図のようになります。

【解答】

(a)解答：(3)
ケーブルの最大使用電圧\( \ E_{\mathrm {m}} \ \)は，
\[
\begin{eqnarray}
E_{\mathrm {m}}&=&\frac {1.15}{1.1}\times 6600 \\[ 5pt ] &=&6900 \ \mathrm {[ V ] } \\[ 5pt ] \end{eqnarray}
\] となるので，試験電圧\( \ V_{\mathrm {t}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {t}}&=&1.5\times E_{\mathrm {m}} \\[ 5pt ] &=&1.5\times 6900 \\[ 5pt ] &=&10350 \ \mathrm {[ V ] } \\[ 5pt ] \end{eqnarray}
\] となる。ケーブルの静電容量\( \ C \ \)は，
\[
\begin{eqnarray}
C&=&0.45\times 87\times 10^{-3} \\[ 5pt ] &=&0.03915 \ \mathrm {[ \mu F ] }
\end{eqnarray}
\] となるので，試験時のケーブルの合成サセプタンス\( \ B \ \)は，三相の並列回路となるから，
\[
\begin{eqnarray}
B&=&3\omega C \\[ 5pt ] &=&3\times 2\pi f C \\[ 5pt ] &=&3\times 2\pi \times 50 \times 0.03915 \\[ 5pt ] &≒&36.898 \ \mathrm {[ \mu S ] } \\[ 5pt ] \end{eqnarray}
\] となる。よって，試験電圧を掛けた際，電流計を流れる電流\(I\)は，
\[
\begin{eqnarray}
I&=&B V_{\mathrm {t}} \\[ 5pt ] &=&36.898\times 10^{-6}\times 10350 \\[ 5pt ] &≒&0.3819 \ \mathrm {[ A ] } \\[ 5pt ] \end{eqnarray}
\] となる。したがって，交流絶縁耐力試験に必要な皮相電力\(S\)は，
\[
\begin{eqnarray}
S&=&V_{\mathrm {t}}I \\[ 5pt ] &=&10350\times 0.3819 \\[ 5pt ] &≒&3953 \ \mathrm {[ V\cdot A ] }　→　4.0 \ \mathrm {[ kV\cdot A ] } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
試験の実施方法として，ケーブルには試験電圧と試験電流を与え，変圧器を流れる電流が小さくなるように調整しなければならない。したがって，ケーブルと並列に接続する必要がある。図の\( \ \mathrm {A}\)-\(\mathrm {C} \ \)間にリアクトルを接続すれば，リアクトルに遅相電流が流れ，試験容量を小さくすることができる。
高圧補償リアクトルのリアクタンス\( \ X_{\mathrm {L}} \ \)は，
\[
\begin{eqnarray}
X_{\mathrm {L}}&=&\frac {12000}{0.292} \\[ 5pt ] &≒&41096 \ \mathrm {[ \Omega ] }
\end{eqnarray}
\] であるから，試験電圧をかけた際の高圧補償リアクトルに流れる電流\( \ I_{\mathrm {L}} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {L}}&=&\frac {V_{\mathrm {t}}}{X_{\mathrm {L}}} \\[ 5pt ] &=&\frac {10350}{41096} \\[ 5pt ] &≒&0.2518 \ \mathrm {[ A ] } \\[ 5pt ] \end{eqnarray}
\] となる。したがって，変圧器に流れる電流\( \ I_{\mathrm {T}} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {T}}&=&I-I_{\mathrm {L}} \\[ 5pt ] &=&0.3819-0.2518 \\[ 5pt ] &≒&0.1301 \ \mathrm {[ A ] } \\[ 5pt ] \end{eqnarray}
\] となるので，変圧器にかかる皮相電力\( \ S_{\mathrm {T}} \ \)は，
\[
\begin{eqnarray}
S_{\mathrm {T}}&=&V_{\mathrm {t}}I_{\mathrm {T}} \\[ 5pt ] &=&10350\times 0.1301\\[ 5pt ] &≒&1347 \ \mathrm {[ V\cdot A ] }　→　1.35 \ \mathrm {[ kV\cdot A ] }　\\[ 5pt ] \end{eqnarray}
\] と求められる。したがって，条件を満たす変圧器の容量は\( \ \mathrm {2 \ kV\cdot A} \ \)となる。