《法規》〈電気施設管理〉[R05下:問12]コンデンサ設備接続による力率改善に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

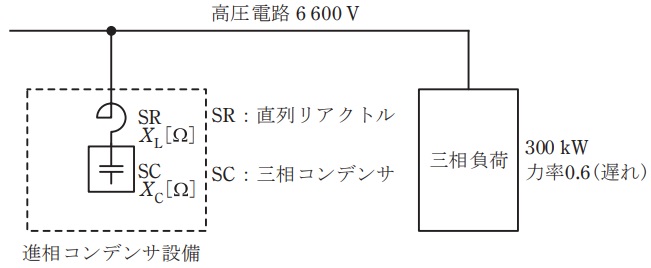
三相$\ 3 \ $線式の高圧電路に$\ 300 \ \mathrm {kW} \ $，遅れ力率$\ 0.6 \ $の三相負荷が接続されている。この負荷と並列に進相コンデンサ設備を接続して力率改善を行うものとする。進相コンデンサ設備は図に示すように直列リアクトル付三相コンデンサとし，直列リアクトル$\ \mathrm {SR} \ $のリアクタンス$\ X_{\mathrm {L}} \ \mathrm {[\Omega ]} \ $は，三相コンデンサ$\ \mathrm {SC} \ $のリアクタンス$\ X_{\mathrm {C}} \ \mathrm {[\Omega ]} \ $の$\ 6 \ \mathrm {％} \ $とするとき，次の(a)及び(b)の問に答えよ。

ただし，高圧電路の線間電圧は$\ 6 \ 600 \ \mathrm {V} \ $とし，無効電力によって電圧は変動しないものとする。

(a)　進相コンデンサ設備を高圧電路に接続したときに三相コンデンサ$\ \mathrm {SC} \ $の端子電圧の値$\ \mathrm {[V]} \ $として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　$\ 6 \ 410 \ $　　(2)　$\ 6 \ 795 \ $　　(3)　$\ 6 \ 807 \ $　　(4)　$\ 6 \ 995 \ $　　(5)　$\ 7 \ 021 \ $

(b)　進相コンデンサを負荷と並列に接続し，力率を遅れ$\ 0.6 \ $から遅れ$\ 0.8 \ $に改善した。このとき，この設備の三相コンデンサ$\ \mathrm {SC} \ $の容量の値$\ \mathrm {[kvar]} \ $として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　$\ 170 \ $　　(2)　$\ 180 \ $　　(3)　$\ 186 \ $　　(4)　$\ 192 \ $　　(5)　$\ 208 \ $

【ワンポイント解説】

コンデンサ設備接続による力率改善に関する問題です。
力率改善の問題は電気施設管理の分野の中でもかなり出題されやすい分野です。本問は直列リアクトルが含まれているので例年の力率改善の問題よりは難易度は幾分高めとなりますが，ベクトル図を描く等解法自体はそれほど変わりませんので，必ずマスターするようにして下さい。
本問は令和元年問12からの再出題となります。

1.抵抗，コイル，コンデンサの電圧$\ V \ \mathrm {[V]} \ $と電流$\ I \ \mathrm {[A]} \ $の関係
抵抗$\ R \ \mathrm {[\Omega ]} \ $，コイル$\ L \ \mathrm {[H]} \ $，コンデンサ$\ C \ \mathrm {[F]} \ $があり，電源の角周波数$\ \omega \ \mathrm {[rad / s]} \ $及び周波数$\ f \ \mathrm {[Hz]} \ $が与えられているとき，それぞれのインピーダンスは，
$$\begin{eqnarray} {\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ] {\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ] {\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}$$ で求められ，それぞれの電圧と電流の関係は，
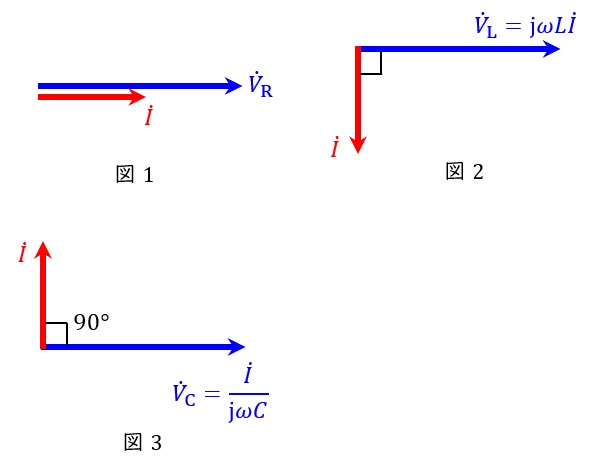
$$\begin{eqnarray} {\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ] {\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ] {\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ] \end{eqnarray}$$ となります。この関係をベクトル図に表すと，図1～図3となります。

2.有効電力$\ P \ \mathrm {[W]} \ $と無効電力$\ Q \ \mathrm {[var]} \ $
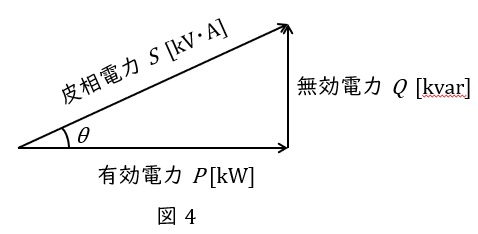
抵抗で消費される電力を有効電力$\ P \ \mathrm {[W]} \ $，リアクタンスで消費もしくは供給される電力を無効電力$\ Q \ \mathrm {[var]} \ $と呼び，図4のようにベクトル図を描きます。さらに，有効電力$\ P \ \mathrm {[W]} \ $と無効電力$\ Q \ \mathrm {[var]} \ $のベクトル和は皮相電力$\ S \ \mathrm {[V\cdot A]} \ $と呼ばれ，
$$\begin{eqnarray} S&=&\sqrt {P^{2}+Q^{2}} \\[ 5pt ] \end{eqnarray}$$ の関係があります。図4において，力率は$\ \cos \theta \ $で定義され，
$$\begin{eqnarray} \cos \theta &=&\frac {P}{S} \\[ 5pt ] \end{eqnarray}$$ となります。

また，線路に電流$\ I \ \mathrm {[A]} \ $が流れているとき，皮相電力$\ S \ \mathrm {[V\cdot A]} \ $，有効電力$\ P \ \mathrm {[W]} \ $，無効電力$\ Q \ \mathrm {[var]} \ $は，インピーダンスを$\ Z \ \mathrm {[\Omega ]} \ $，抵抗を$\ R \ \mathrm {[\Omega ]} \ $，リアクタンスを$\ X \ \mathrm {[\Omega ]} \ $とすると，
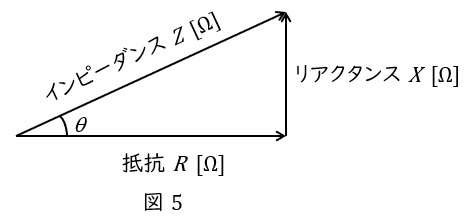
$$\begin{eqnarray} S &=&ZI^{2} \\[ 5pt ] P &=&RI^{2} \\[ 5pt ] Q &=&XI^{2} \\[ 5pt ] \end{eqnarray}$$ となるため，$\ Z \ \mathrm {[\Omega ]} \ $，$\ R \ \mathrm {[\Omega ]} \ $，$\ X \ \mathrm {[\Omega ]} \ $に関しても電力と同様な図5のような関係を描くことができます。

3.分圧・分流の法則
①分圧の法則
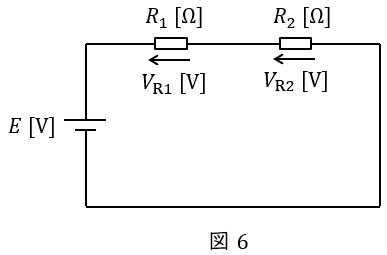
図6に示した直列回路において，各抵抗にかかる電圧は以下の通りとなります。
$$\begin{eqnarray} V_{\mathrm {R1}}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ] V_{\mathrm {R2}}&=&\frac {R_{2}}{R_{1}+R_{2}}E \\[ 5pt ] \end{eqnarray}$$

②分流の法則
図7に示した並列回路において，各抵抗に流れる電流は以下の通りとなります。分子の抵抗が分圧の法則と逆となることに注意して下さい。
$$\begin{eqnarray} I_{\mathrm {R1}}&=&\frac {\color{red}{R_{2}}}{R_{1}+R_{2}}I \\[ 5pt ] I_{\mathrm {R2}}&=&\frac {\color{red}{R_{1}}}{R_{1}+R_{2}}I \\[ 5pt ] \end{eqnarray}$$

【解答】

(a)解答：(5)
進相コンデンサ設備を高圧電路に接続したときの三相コンデンサ$\ \mathrm {SC} \ $の端子電圧$\ V_{\mathrm {C}} \ \mathrm {[V]} \ $は，高圧電路の線間電圧を$\ V_{\mathrm {n}}=6 \ 600 \ \mathrm {[V]} \ $とすると，ワンポイント解説「1.抵抗，コイル，コンデンサの電圧$\ V \ \mathrm {[V]} \ $と電流$\ I \ \mathrm {[A]} \ $の関係」及び「3.分圧・分流の法則」より，
$$\begin{eqnarray} V_{\mathrm {C}}&=&\frac {-\mathrm {j}X_{\mathrm {C}}}{\mathrm {j}X_{\mathrm {L}}-\mathrm {j}X_{\mathrm {C}}}V_{\mathrm {n}} \\[ 5pt ] &=&\frac {-X_{\mathrm {C}}}{X_{\mathrm {L}}-X_{\mathrm {C}}}V_{\mathrm {n}} \\[ 5pt ] \end{eqnarray}$$ となり，$\ X_{\mathrm {L}} \ \mathrm {[\Omega ]} \ $は，$\ X_{\mathrm {C}} \ \mathrm {[\Omega ]} \ $の$\ 6 \ \mathrm {[％]} \ $，すなわち$\ X_{\mathrm {L}}=0.06X_{\mathrm {C}} \ $であることに注意すれば，
$$\begin{eqnarray} V_{\mathrm {C}}&=&\frac {-X_{\mathrm {C}}}{0.06X_{\mathrm {C}}-X_{\mathrm {C}}}V_{\mathrm {n}} \\[ 5pt ] &=&\frac {-1}{0.06-1}\times 6 \ 600 \\[ 5pt ] &≒&7 \ 021 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(b)解答：(3)
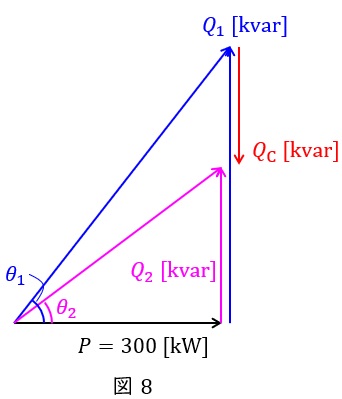
進相コンデンサ設備接続前後のベクトル図を図8に示す。図8より接続前後の無効電力$\ Q_{1} \ \mathrm {[kvar]} \ $及び$\ Q_{2} \ \mathrm {[kvar]} \ $は，三相負荷の有効電力が$\ P=300 \ \mathrm {[kW]} \ $，コンデンサ設備接続前後の力率がそれぞれ$\ \cos \theta _{1}=0.6 \ $，$\ \cos \theta _{2}=0.8 \ $なので，ワンポイント解説「2.有効電力$\ P \ \mathrm {[W]} \ $と無効電力$\ Q \ \mathrm {[var]} \ $」の通り，
$$\begin{eqnarray} Q_{1}&=&P\tan \theta _{1} \\[ 5pt ] &=&P\frac {\sin \theta _{1}}{\cos \theta _{1}} \\[ 5pt ] &=&P\frac {\sqrt {1-\cos ^{2}\theta _{1}}}{\cos \theta _{1}} \\[ 5pt ] &=&300\times \frac {\sqrt {1-0.6^{2}}}{0.6} \\[ 5pt ] &=&300\times \frac {0.8}{0.6} \\[ 5pt ] &=&400 \ \mathrm {[kvar]} \\[ 5pt ] Q_{2}&=&P\tan \theta _{2} \\[ 5pt ] &=&P\frac {\sin \theta _{2}}{\cos \theta _{2}} \\[ 5pt ] &=&P\frac {\sqrt {1-\cos ^{2}\theta _{2}}}{\cos \theta _{2}} \\[ 5pt ] &=&300\times \frac {\sqrt {1-0.8^{2}}}{0.8} \\[ 5pt ] &=&300\times \frac {0.6}{0.8} \\[ 5pt ] &=&225 \ \mathrm {[kvar]} \\[ 5pt ] \end{eqnarray}$$ となり，進相コンデンサによる無効電力の供給容量$\ Q_{\mathrm {C}} \ \mathrm {[kvar]} \ $は，
$$\begin{eqnarray} Q_{\mathrm {C}}&=&Q_{1}-Q_{2} \\[ 5pt ] &=&400-225 \\[ 5pt ] &=&175 \ \mathrm {[kvar]} \\[ 5pt ] \end{eqnarray}$$ となる。ここで，進相コンデンサ設備には$\ 6 \ \mathrm {[％]} \ $の直列リアクトルのリアクタンス$\ X_{\mathrm {L}} \ \mathrm {[\Omega ]} \ $が接続されているので，三相コンデンサ$\ \mathrm {SC} \ $の容量$\ Q_{\mathrm {SC}} \ \mathrm {[kvar]} \ $は，
$$\begin{eqnarray} Q_{\mathrm {SC}}&=&\frac {-\mathrm {j}X_{\mathrm {C}}}{\mathrm {j}X_{\mathrm {L}}-\mathrm {j}X_{\mathrm {C}}}\times Q_{\mathrm {C}} \\[ 5pt ] &=&\frac {-X_{\mathrm {C}}}{X_{\mathrm {L}}-X_{\mathrm {C}}}\times Q_{\mathrm {C}} \\[ 5pt ] &=&\frac {-X_{\mathrm {C}}}{0.06X_{\mathrm {C}}-X_{\mathrm {C}}}\times Q_{\mathrm {C}} \\[ 5pt ] &=&\frac {-1}{0.06-1}\times 175 \\[ 5pt ] &≒&186 \ \mathrm {[kvar]} \\[ 5pt ] \end{eqnarray}$$ と求められる。