Contents
【問題】
【難易度】★☆☆☆☆(易しい)
図のように,正弦波交流電圧\( \ e=E_{m} \sin \omega t \ \mathrm {[V]} \ \)の電源,静電容量\( \ C \ \mathrm {[F]} \ \)のコンデンサ及びインダクタンス\( \ L \ \mathrm {[H]} \ \)のコイルからなる交流回路がある。この回路に流れる電流\( \ i \ \mathrm {[A]} \ \)が常に零となるための角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)の値を表す式として,正しいのは次のうちどれか。
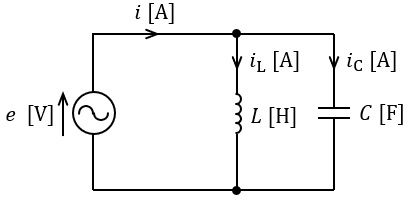
(1) \( \ \displaystyle \frac {1}{\sqrt {LC}} \ \) (2) \( \ \sqrt {LC} \ \) (3) \( \ \displaystyle \frac {1}{LC} \ \) (4) \( \ \displaystyle \sqrt {\frac {L}{C}} \ \) (5) \( \ \displaystyle \sqrt {\frac {C}{L}} \ \)
【ワンポイント解説】
\( \ LC \ \)並列回路に流れる電流が零となる,すなわち並列共振する際の角周波数を求める問題です。
もちろん導出できるのが理想ですが,共振角周波数及び共振周波数においては値を覚えておくことも重要です。本問の内容とは直接関係はありませんが,直列共振に関しても合わせて理解しておきましょう。
1.直列回路の共振回路
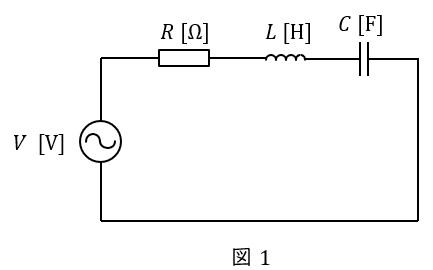
図1のような\( \ RLC \ \)直列回路があった場合の合成インピーダンス\( \ \dot Z \ \mathrm {[\Omega ]} \ \)は,角周波数を\( \ \omega \ \mathrm {[rad / s]} \ \)とすると,
\[
\begin{eqnarray}
\dot Z&=&R+\mathrm {j}\omega L +\frac {1}{\mathrm {j}\omega C} \\[ 5pt ]
&=&R+\mathrm {j}\left( \omega L -\frac {1}{\omega C}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,インピーダンスが最も小さくなるためには,上式の虚数部が零である必要があります。よって,共振角周波数\( \ \omega _{\mathrm {c}} \ \mathrm {[rad / s]} \ \)は,
\[
\begin{eqnarray}
\omega_{\mathrm {c}} L -\frac {1}{\omega_{\mathrm {c}} C}&=&0 \\[ 5pt ]
\omega_{\mathrm {c}} L &=&\frac {1}{\omega_{\mathrm {c}} C} \\[ 5pt ]
\omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ]
\omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ]
\end{eqnarray}
\]
となります。また,共振周波数を\( \ f_{\mathrm {c}} \ \mathrm {[Hz]} \ \)とすると,\( \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ \)より,
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
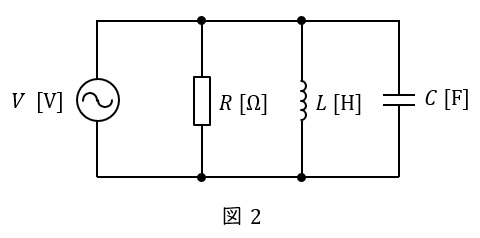
2.並列回路の共振回路
図2のような\( \ RLC \ \)並列回路があった場合の合成アドミタンス\( \ \dot Y \ \mathrm {[S]} \ \)は,角周波数を\( \ \omega \ \mathrm {[rad / s]} \ \)とすると,
\[
\begin{eqnarray}
\dot Y&=&\frac {1}{R}+\mathrm {j}\omega C +\frac {1}{\mathrm {j}\omega L} \\[ 5pt ]
&=&\frac {1}{R}+\mathrm {j}\left( \omega C -\frac {1}{\omega L}\right)
\end{eqnarray}
\]
となり,アドミタンスが最も小さくなるためには,上式の虚数部が零である必要があります。よって,共振角周波数\( \ \omega _{\mathrm {c}} \ \mathrm {[rad / s]} \ \)は,
\[
\begin{eqnarray}
\omega_{\mathrm {c}} C -\frac {1}{\omega_{\mathrm {c}} L}&=&0 \\[ 5pt ]
\omega_{\mathrm {c}} C &=&\frac {1}{\omega_{\mathrm {c}} L} \\[ 5pt ]
\omega_{\mathrm {c}}^{2} &=&\frac {1}{LC} \\[ 5pt ]
\omega_{\mathrm {c}} &=& \frac {1}{\sqrt {LC}} \\[ 5pt ]
\end{eqnarray}
\]
となります。また,共振周波数を\( \ f_{\mathrm {c}} \ \mathrm {[Hz]} \ \)とすると,\( \ \omega _{\mathrm {c}}=2\pi f_{\mathrm {c}} \ \)より,
\[
\begin{eqnarray}
f_{\mathrm {c}} &=& \frac {1}{2\pi \sqrt {LC}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
解答:(1)
ワンポイント解説「2.並列回路の共振回路」の通り,回路に流れる電流\( \ i \ \mathrm {[A]} \ \)が常に零となるための角周波数,すなわち共振角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)は,
\[
\begin{eqnarray}
\omega &=& \frac {1}{\sqrt {LC}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは