《理論》〈電気回路〉[H20:問10]RL直列回路の過渡現象に関する論説問題

【問題】

【難易度】★☆☆☆☆（易しい）

図のように，開いた状態のスイッチ\( \ \mathrm {S} \ \)，\( \ R \ \mathrm {[\Omega ]} \ \)の抵抗，インダクタンス\( \ L \ \mathrm {[H]} \ \)のコイル，直流電源\( \ E \ \mathrm {[V]} \ \)からなる直列回路がある。この直列回路において，スイッチ\( \ \mathrm {S} \ \)を閉じた直後に過渡現象が起こる。この場合に「回路に流れる電流」，「抵抗の端子電圧」及び「コイルの端子電圧」に関し，時間の経過にしたがって起こる過渡現象として，正しいものを組み合わせたのは次のうちどれか。

\[
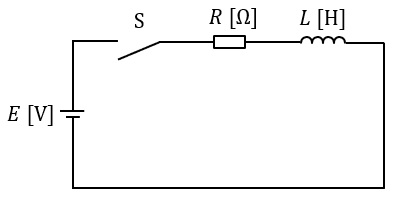
\begin{array}{cccc}
& 回路に流れる電流 & 抵抗の端子電圧 & コイルの端子電圧 \\
\hline
(1) & 　大きくなる　 & 　低下する　 & 　上昇する　 \\
\hline
(2) & 　小さくなる　 & 　上昇する　 & 　低下する　 \\
\hline
(3) & 　大きくなる　 & 　上昇する　 & 　上昇する　 \\
\hline
(4) & 　小さくなる　 & 　低下する　 & 　上昇する　 \\
\hline
(5) & 　大きくなる　 & 　上昇する　 & 　低下する　 \\
\hline
\end{array}
\]

【ワンポイント解説】

\( \ RL \ \)直列回路の過渡現象を問う問題です。
リアクトルがどのような作用をするか理解しているかどうかが問われています。一度理解してしまえば様々な問題に対応できるようになるため，リアクトルとコンデンサの特性はここで理解しておくようにしましょう。

1.過渡現象におけるリアクトルの過渡状態と定常状態
開いた状態である\( \ RL \ \)直列回路のスイッチを投入した後の変化は以下のように考えます。

① 過渡状態
リアクトルに流れる電流値を維持しようとする働きをします。したがって，リアクトルに電圧を印加した瞬間はほとんど電流は流れないので，開放として考えます。

② 定常状態
電圧を印加して十分時間が経過した後は，リアクトルの抵抗はほぼ零になります。したがって，短絡として考えます。

2.過渡現象におけるコンデンサの過渡状態と定常状態
開いた状態である\( \ RC \ \)直列回路のスイッチを投入した後の変化は以下のように考えます。

① 過渡状態
コンデンサに蓄えられている電荷が零であるので，電流がものすごく流れやすい状態，すなわち短絡として考えます。

② 定常状態
コンデンサに十分に電荷が蓄えられているので，電流をこれ以上蓄えようとしない，すなわち開放として考えます。

【解答】

解答：(5)
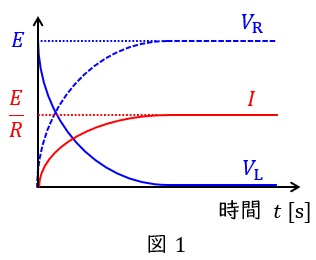
ワンポイント解説「1.過渡現象におけるリアクトルの過渡状態と定常状態」の通り，以下に示す特性から，図1に示すような波形を描くことになります。

回路に流れる電流
スイッチ\( \ \mathrm {S} \ \)投入直後はリアクトル\( \ L \ \mathrm {[H]} \ \)により回路には電流が流れず，十分に時間が経過するとリアクトル\( \ L \ \mathrm {[H]} \ \)は短絡状態となり，回路には\( \ \displaystyle I=\frac {E}{R} \ \mathrm {[A]} \ \)の電流が流れます。したがって，徐々に大きくなることがわかります。

抵抗の端子電圧
抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の端子電圧\( \ V_{\mathrm {R}} \ \mathrm {[V]} \ \)は，\( \ V_{\mathrm {R}}=RI \ \)の関係から，電流と同様な波形を描き徐々に上昇することになります。

コイルの端子電圧
リアクトル\( \ L \ \mathrm {[H]} \ \)の端子電圧\( \ V_{\mathrm {L}} \ \mathrm {[V]} \ \)は，\( \ V_{\mathrm {L}}=E-V_{\mathrm {R}} \ \)の関係から，徐々に低下することになります。