Contents
【問題】
【難易度】★★★★☆(やや難しい)
図の交流回路において,回路素子は,インダクタンス\( \ L \ \)のコイル又は静電容量\( \ C \ \)のコンデンサである。この回路に正弦波交流電圧\( \ v=500 \sin \left( 1 \ 000 t\right) \ \mathrm {[V]} \ \)を加えたとき,回路に流れる電流は,\( \ i= -50 \cos \left( 1 \ 000 t \right) \ \mathrm {[A]} \ \)であった。このとき,次の(a)及び(b)の問に答えよ。
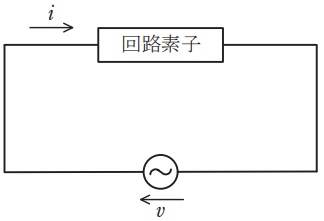
(a) 回路素子の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ C=10 \ \mathrm {nF} \ \) (2) \( \ C=100 \ \mathrm {nF} \ \) (3) \( \ C=10 \ \mathrm {\mu F} \ \)
(4) \( \ L=10 \ \mathrm {mH} \ \) (5) \( \ L=100 \ \mathrm {mH} \ \)
(b) この回路素子に蓄えられるエネルギーの最大値\( \ W_{\mathrm {max}} \ \)の値\( \ \mathrm {[J]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,インダクタンスの場合には\( \ \displaystyle \frac {1}{2}Li^{2} \ \)の,静電容量の場合には\( \ \displaystyle \frac {1}{2}Cv^{2} \ \)のエネルギーが蓄えられるものとする。
(1) \( \ 2.5 \ \) (2) \( \ 6.25 \ \) (3) \( \ 12.5 \ \) (4) \( \ 25 \ \) (5) \( \ 125 \ \)
【ワンポイント解説】
瞬時値の値から回路のインダクタンスと蓄えられるエネルギーを問う問題です。
恐らく多くの受験生が苦手とする分野で正答率も低かったと予想されます。コツを掴んで理解するようにしましょう。
本問は平成17年問16の再出題となります。
1.抵抗,コイル,コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係
抵抗\( \ R \ \mathrm {[\Omega ]} \ \),コイル\( \ L \ \mathrm {[H]} \ \),コンデンサ\( \ C \ \mathrm {[F]} \ \)があり,電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)及び周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき,それぞれのインピーダンスは,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ]
{\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ]
{\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ]
\end{eqnarray}
\]
で求められ,それぞれの電圧と電流の関係は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ]
{\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ]
{\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ]
\end{eqnarray}
\]
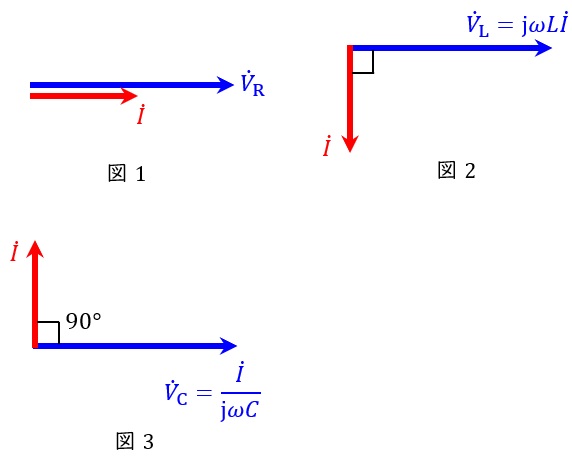
となります。この関係をベクトル図に表すと,図1~図3となります。
2.正弦波交流の基本
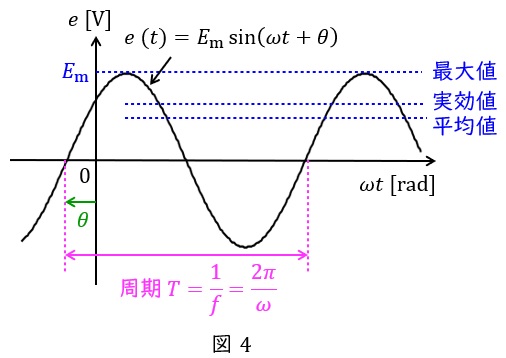
正弦波交流は図4に示されるような波形の交流です。
振幅の大きさ(最大値)を\( \ E_{\mathrm {m}} \ \mathrm {[V]} \ \),角速度を\( \ \omega \ \mathrm {[rad / s]} \ \),時間を\( \ t \ \mathrm {[s]} \ \),初期位相を\( \ \theta \ \mathrm {[rad]} \ \)とすれば,瞬時値\( \ e\left( t \right) \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
e\left( t \right) &=&E_{\mathrm {m}}\sin \left( \omega t +\theta \right) \\[ 5pt ]
\end{eqnarray}
\]
となり,波形の周期\( \ T \ \mathrm {[s]} \ \)は,周波数を\( \ f \ \mathrm {[Hz]} \ \)とすると,
\[
\begin{eqnarray}
T &=&\frac {1}{f}=\frac {2\pi }{\omega } \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,\( \ \omega =2\pi f \ \)となり,
\[
\begin{eqnarray}
e\left( t \right) &=&E_{\mathrm {m}}\sin \left( 2\pi f t +\theta \right) \\[ 5pt ]
\end{eqnarray}
\]
と表現することもできます。
3.平均値と実効値の定義
\( \ f( \theta ) \ \)を周期\( \ T \ \)の周期関数であるとしたとき,平均値と実効値は以下の通りとなります。
①平均値\( \ F_{\mathrm {av}} \ \)
定義式は,
\[
\begin{eqnarray}
F_{\mathrm {av}}&=&\frac {1}{T}\int _{0}^{T}f( \theta ) \mathrm {d}\theta \\[ 5pt ]
\end{eqnarray}
\]
であり,これを正弦波\( \ e\left( t \right) =E_{\mathrm {m}}\sin \omega t \ \)に適用すると,
\[
\begin{eqnarray}
E_{\mathrm {av}} &=&\frac {1}{\pi }\int _{0}^{\pi }E_{\mathrm {m}}\sin \omega t \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {E_{\mathrm {m}}}{\pi }\left[ -\cos \omega t \right] _{0}^{\pi } \\[ 5pt ]
&=&\frac {E_{\mathrm {m}}}{\pi }\left[ 1+1 \right] \\[ 5pt ]
&=&\frac {2}{\pi }E_{\mathrm {m}}
\end{eqnarray}
\]
となります。
②実効値\( \ F \ \)
定義式は,
\[
\begin{eqnarray}
F&=&\sqrt {\frac {1}{T} \int _{0}^{T} f( \theta ) ^{2} \mathrm {d}\theta } \\[ 5pt ]
\end{eqnarray}
\]
であり,これを正弦波\( \ e\left( t \right) =E_{\mathrm {m}}\sin \omega t \ \)に適用すると,
\[
\begin{eqnarray}
E &=&\sqrt {\frac {1}{\pi }\int _{0}^{\pi }{E_{\mathrm {m}}}^{2}\sin ^{2}\omega t \mathrm {d}\omega t} \\[ 5pt ]
&=&E_{\mathrm {m}}\sqrt {\frac {1}{\pi }\int _{0}^{\pi }\frac {1-\cos 2\omega t}{2} \mathrm {d}\omega t} \\[ 5pt ]
&=&E_{\mathrm {m}}\sqrt {\frac {1}{\pi }\left[ \frac {1}{2}\omega t -\frac {1}{4}\sin 2\omega t \right] _{0}^{\pi } } \\[ 5pt ]
&=&E_{\mathrm {m}}\sqrt {\frac {1}{\pi }\left[ \frac {1}{2}\pi -0 -0 +0 \right] _{0}^{\pi } } \\[ 5pt ]
&=&\frac {E_{\mathrm {m}}}{\sqrt {2}}
\end{eqnarray}
\]
となります。
4.\( \sin \ \)と\( \ \cos \ \)の関係
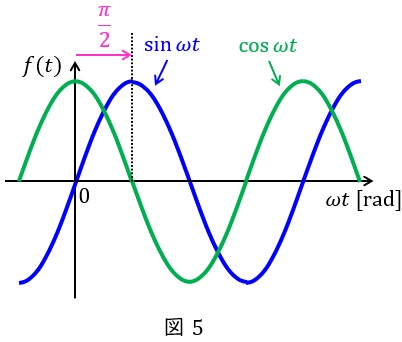
\( \ f(t)=\sin \omega t \ \)と\( \ f(t)=\cos \omega t \ \)をグラフに示すと図5のようになります。
グラフを比較すると,\( \ \displaystyle \sin \frac {\pi }{2} =\cos 0 \ \)すなわち\( \ \displaystyle \sin \left( \omega t+\frac {\pi }{2}\right) =\cos \omega t \ \)の関係があることがわかります。
【解答】
(a)解答:(4)
電流\( \ i= -50 \cos \left( 1 \ 000 t \right) \ \mathrm {[A]} \ \)を変形すると,ワンポイント解説「4.\( \sin \ \)と\( \ \cos \ \)の関係」の通り,
\[
\begin{eqnarray}
i&=&-50 \cos \left( 1 \ 000 t \right) \\[ 5pt ]
&=&-50 \sin \left( 1 \ 000 t+\frac {\pi }{2} \right) \\[ 5pt ]
&=&50 \sin \left( 1 \ 000 t-\frac {\pi }{2} \right) \left( ∵ \sin \frac {\pi }{2} =-\sin \left( -\frac {\pi }{2}\right) \ ⇒ \ \sin \left( \omega t+\frac {\pi }{2}\right) =-\sin \left( \omega t-\frac {\pi }{2}\right)\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,電流\( \ i \ \mathrm {[A]} \ \)は電圧\( \ v \ \mathrm {[V]} \ \)より\( \ \displaystyle \frac {\pi }{2} \ \mathrm {[rad]} \ \)遅れとなるので,回路素子はインダクタンス\( \ L \ \)と求められる。
次にインダクタンスの大きさを求めていくと,ワンポイント解説「3.平均値と実効値の定義」より,電圧の実効値\( \ \displaystyle V=\frac {500}{\sqrt {2}} \ \mathrm {[V]} \ \),電流の実効値\( \ \displaystyle I=\frac {50}{\sqrt {2}} \ \mathrm {[A]} \ \),角周波数\( \ \omega =1 \ 000 \ \mathrm {[rad / s]} \ \)なので,ワンポイント解説「1.抵抗,コイル,コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係」の通り,
\[
\begin{eqnarray}
\omega L&=&\frac {V}{I} \\[ 5pt ]
1000 L&=&\frac {\displaystyle \frac {500}{\sqrt {2}}}{\displaystyle \frac {50}{\sqrt {2}}} \\[ 5pt ]
L&=&0.01 \ \mathrm {[H]} → 10 \ \mathrm {[mH]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(3)
インダクタンス\( \ L \ \)に蓄えられるエネルギーの最大値\( \ W_{\mathrm {max}} \ \mathrm {[J]} \ \)は,電流の最大値を使用すれば良いので,
\[
\begin{eqnarray}
W_{\mathrm {max}}&=&\frac {1}{2}Li^{2} \\[ 5pt ]
&=&\frac {1}{2}\times 0.01\times 50^{2} \\[ 5pt ]
&=&12.5 \ \mathrm {[J]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは