《理論》〈電気回路〉[H27:問16]合成静電容量の導出に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図1の端子\( \ \mathrm {a-d} \ \)間の合成静電容量について，次の(a)及び(b)の問に答えよ。

(a)　端子\( \ \mathrm {b-c-d} \ \)間は図2のように\( \ \Delta \ \)結線で接続されている。これを図3のように\( \ \mathrm {Y} \ \)結線に変換したとき，電気的に等価となるコンデンサ\( \ C \ \)の値\( \ \mathrm {[\mu F]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 1.0 \ \)　　(2)　\( \ 2.0 \ \)　　(3)　\( \ 4.5 \ \)　　(4)　\( \ 6.0 \ \)　　(5)　\( \ 9.0 \ \)

(b)　図3を用いて，図1の端子\( \ \mathrm {b-c-d} \ \)間を\( \ \mathrm {Y} \ \)結線回路に変換したとき，図1の端子\( \ \mathrm {a-d} \ \)間の合成静電容量\( \ C_{0} \ \)の値\( \ \mathrm {[\mu F]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 3.0 \ \)　　(2)　\( \ 4.5 \ \)　　(3)　\( \ 4.8 \ \)　　(4)　\( \ 6.0 \ \)　　(5)　\( \ 9.0 \ \)

【ワンポイント解説】

\( \ \Delta -\mathrm {Y} \ \)変換の問題は理論科目では毎年のように出題される最頻出問題です。参考書では抵抗での記載が多いと思いますが，リアクタンスでも同じ式を使用できます。三種では不平衡回路の問題は出題されにくいですが，各変換はよく理解しておくようにして下さい。

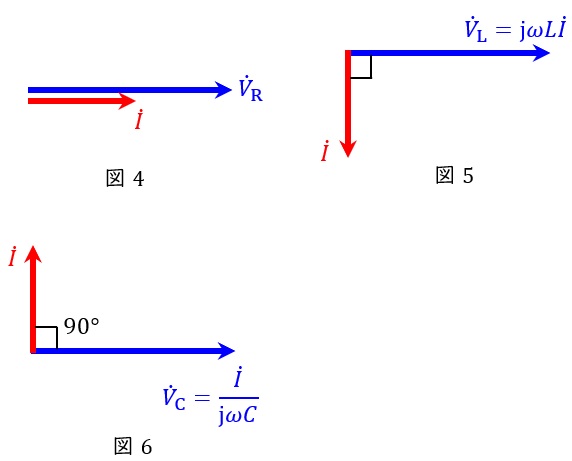
1.抵抗，コイル，コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係
抵抗\( \ R \ \mathrm {[\Omega ]} \ \)，コイル\( \ L \ \mathrm {[H]} \ \)，コンデンサ\( \ C \ \mathrm {[F]} \ \)があり，電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)及び周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき，それぞれのインピーダンスは，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ] {\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ] {\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}
\] で求められ，それぞれの電圧と電流の関係は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ] {\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ] {\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ] \end{eqnarray}
\] となります。この関係をベクトル図に表すと，図4～図6となります。

2.コンデンサの合成静電容量
静電容量\( \ C_{1} \ \mathrm {[F]} \ \)と\( \ C_{2} \ \mathrm {[F]} \ \)の合成静電容量\( \ C \ \mathrm {[F]} \ \)は，
　　並列接続時：\( \ C=C_{1}+C_{2} \ \)
　　直列接続時：\( \ \displaystyle C=\frac {1}{\displaystyle \frac {1}{C_{1}}+\frac {1}{C_{2}}}=\frac {C_{1}C_{2}}{C_{1}+C_{2}} \ \)
となります。

3.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換
①\( \ \Delta -\mathrm {Y} \ \)変換
図7において，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}}&=&\frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] {\dot Z}_{\mathrm {b}}&=&\frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] {\dot Z}_{\mathrm {c}}&=&\frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] \end{eqnarray}
\] ②\( \ \mathrm {Y}-\Delta \ \)変換
図7において，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ] {\dot Z}_{\mathrm {bc}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ] {\dot Z}_{\mathrm {ca}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ] \end{eqnarray}
\] 平衡三相回路においては，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}={\dot Z}_{\mathrm {bc}}&=&{\dot Z}_{\mathrm {ca}}=3{\dot Z}_{\mathrm {a}}=3{\dot Z}_{\mathrm {b}}=3{\dot Z}_{\mathrm {c}} \\[ 5pt ] \end{eqnarray}
\] となります。

【関連する「電気の神髄」記事】

　　Y⇔Δ回路のインピーダンス変換式

【解答】

(a)解答：(5)
ワンポイント解説「3.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換」の通り，三相平衡回路での\( \ \mathrm {Y} \ \)接続時のインピーダンスは\( \ \Delta \ \)接続時の\( \ \displaystyle \frac {1}{3} \ \)倍となるから，
\[
\begin{eqnarray}
\frac {1}{\mathrm {j}\omega C_{\mathrm {Y}}}&=&\frac {1}{3}\cdot \frac {1}{\mathrm {j}\omega C_{\mathrm {\Delta }}} \\[ 5pt ] \frac {1}{C_{\mathrm {Y}}}&=&\frac {1}{3C_{\mathrm {\Delta }}} \\[ 5pt ] C_{\mathrm {Y}}&=&3C_{\mathrm {\Delta }} \\[ 5pt ] \end{eqnarray}
\] の関係があるので，図2における\( \ C \ \mathrm {[\mu F]} \ \)は，
\[
\begin{eqnarray}
C&=&3\times 3 \\[ 5pt ] &=&9 \ \mathrm {[\mu F]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
(a)の解答を元に図1の回路を整理すると図8のようになる。
\( \ C_{1}=9 \ \mathrm {[\mu F]} \ \)と\( \ C_{3}=9 \ \mathrm {[\mu F]} \ \)の合成静電容量\( \ C_{13} \ \mathrm {[\mu F]} \ \)は，ワンポイント解説「2.コンデンサの合成静電容量」の通り，
\[
\begin{eqnarray}
C_{13}&=&\frac {C_{1}C_{3}}{C_{1}+C_{3}} \\[ 5pt ] &=&\frac {9\times 9}{9+9} \\[ 5pt ] &=&4.5 \ \mathrm {[\mu F]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ C_{2}=18 \ \mathrm {[\mu F]} \ \)と\( \ C_{4}=9 \ \mathrm {[\mu F]} \ \)の合成静電容量\( \ C_{24} \ \mathrm {[\mu F]} \ \)は，ワンポイント解説「2.コンデンサの合成静電容量」の通り，
\[
\begin{eqnarray}
C_{24}&=&\frac {C_{2}C_{4}}{C_{2}+C_{4}} \\[ 5pt ] &=&\frac {18\times 9}{18+9} \\[ 5pt ] &=&6 \ \mathrm {[\mu F]}
\end{eqnarray}
\] となる。よって，\( \ C_{1} \ ～C_{4} \ \)までの合成静電容量\( \ C_{1234} \ \mathrm {[\mu F]} \ \)は，ワンポイント解説「2.コンデンサの合成静電容量」の通り，
\[
\begin{eqnarray}
C_{1234}&=&C_{13}+C_{24} \\[ 5pt ] &=&4.5+6 \\[ 5pt ] &=&10.5 \ \mathrm {[\mu F]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，端子\( \ \mathrm {a-d} \ \)間の合成静電容量\( \ C_{0} \ \mathrm {[\mu F]} \ \)は，ワンポイント解説「2.コンデンサの合成静電容量」の通り，
\[
\begin{eqnarray}
C_{0}&=&\frac {C_{1234}C_{5}}{C_{1234}+C_{5}} \\[ 5pt ] &=&\frac {10.5\times 9}{10.5+9} \\[ 5pt ] &≒&4.84　→　4.8 \ \mathrm {[\mu F]}
\end{eqnarray}
\] と求められる。