Contents
【問題】
【難易度】★★★☆☆(普通)
定格周波数\( \ 60 \ \mathrm {Hz} \ \),\( \ 6 \ \)極の三相巻線形誘導電動機があり,二次巻線を短絡して定格負荷で運転したときの回転速度は\( \ 1 \ 170 \ \mathrm {{min}^{-1}} \ \)である。この電動機について,次の(a)及び(b)の問に答えよ。
ただし,電動機の二次抵抗値が一定のとき,滑りとトルクは比例関係にあるものとする。
(a) この電動機を定格負荷の\( \ 80 \ \mathrm {%} \ \)のトルクで運転する場合,二次巻線が短絡してあるときの滑りの値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 0.015 \ \) (2) \( \ 0.02 \ \) (3) \( \ 0.025 \ \) (4) \( \ 0.03 \ \) (5) \( \ 0.04 \ \)
(b) この電動機を定格負荷の\( \ 80 \ \mathrm {%} \ \)のトルクで運転する場合,二次巻線端子に三相抵抗器を接続し,二次巻線回路の\( \ 1 \ \)相当たりの抵抗値を短絡時の\( \ 2.5 \ \)倍にしたときの回転速度\( \ \mathrm {[{min}^{-1}]} \ \)の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 980 \ \) (2) \( \ 1 \ 110 \ \) (3) \( \ 1 \ 140 \ \) (4) \( \ 1 \ 170 \ \) (5) \( \ 1 \ 200 \ \)
【ワンポイント解説】
三相巻線形誘導電動機の滑りと回転速度を求める問題です。
多くの受験生がトルクの比例推移の公式を理解しているので,(a)が解けると(b)も解ける方が多く点数差が開きやすい問題であったかなと思います。トルクと二次抵抗,滑りの関係は覚えておくようにしましょう。
本問は平成12年問12からの再出題となります。
1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \),電源の周波数が\( \ f \ \mathrm {[Hz]} \ \)の時,同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)は,
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \),回転子の回転速度が\( \ N \ \mathrm {[{min}^{-1}]} \ \)である時,誘導機の滑り\( \ s \ \)は,
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
と定義されます。これを整理すると,
\[
\begin{eqnarray}
sN_{\mathrm {s}} &=&N_{\mathrm {s}}-N \\[ 5pt ]
N &=&N_{\mathrm {s}}-sN_{\mathrm {s}} \\[ 5pt ]
&=&\left( 1-s \right) N_{\mathrm {s}} \\[ 5pt ]
\end{eqnarray}
\]
と同期速度から回転速度が導出できます。
3.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1のようになります。図1において,\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧,\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流,\( \ {\dot I}_{2}^{\prime } \ \mathrm {[A]} \ \)は二次電流の一次換算,\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流,\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗,\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗の一次換算,\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス,\( \ x_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンスの一次換算,\( \ s \ \)は滑りとなります。
図1より,出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \),二次入力\( \ P_{2} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& 3\frac {1-s}{s}r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ]
P_{\mathrm {c2}} &=& 3r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ]
P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =3\frac {r_{2}^{\prime }}{s}{I_{2}^{\prime }}^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,誘導電動機の二次入力\( \ P_{2} \ \mathrm {[W]} \ \),出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \)には,
\[
\begin{eqnarray}
P_{2}:P_{\mathrm {o}}:P_{\mathrm {c2}} &=& 1:(1-s):s \\[ 5pt ]
\end{eqnarray}
\]
の関係があることが分かります。

4.巻線形誘導電動機のトルクの比例推移
図1より,二次電流の一次換算値の大きさ\( \ I_{2}^{\prime } \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{2}^{\prime } &=& \frac {V_{1}}{\sqrt {\left( r_{1}+\displaystyle \frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
であるため,三相誘導電動機のトルク\( \ T \ \mathrm {[N\cdot m]} \ \)は,
\[
\begin{eqnarray}
T&=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ]
&=&\frac {P_{2}\left( 1-s\right) }{\omega _{\mathrm {s}}\left( 1-s\right) } \\[ 5pt ]
&=&\frac {P_{2}}{\omega _{\mathrm {s}} } \\[ 5pt ]
&=&\frac {\displaystyle 3\frac {r_{2}^{\prime }}{s}{I_{2}^{\prime }}^{2}}{\omega _{\mathrm {s}} } \\[ 5pt ]
&=& \frac {1}{\omega _{\mathrm {s}}}\frac {3V_{1}^{2}\displaystyle \frac {r_{2}^{\prime }}{s}}{\left( r_{1}+\displaystyle \frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。\( \ 1≫s \ \)の時,\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)以外の抵抗やリアクタンスは無視できるので,
\[
\begin{eqnarray}
T &≃& \frac {3V_{1}^{2}s}{\omega _{\mathrm {s}}r_{2}^{\prime }} \\[ 5pt ]
\end{eqnarray}
\]
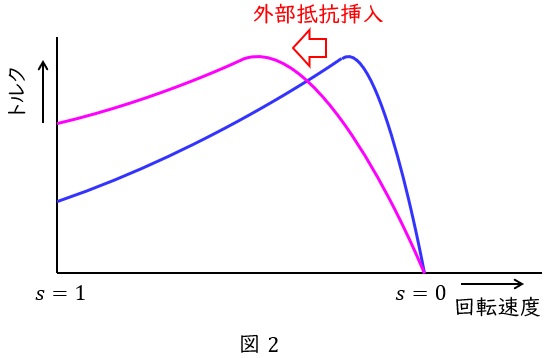
となり,トルクに対する変数は可変抵抗(外部抵抗が挿入可能)である二次抵抗\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)と滑り\( \ s \ \)のみであり,トルク\( \ T \ \mathrm {[N\cdot m]} \ \)を一定とすると,
\[
\begin{eqnarray}
\frac {r_{2}^{\prime }}{s} &=& 一定 \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【解答】
(a)解答:(2)
三相巻線形誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)は,周波数\( \ f=60 \ \mathrm {[Hz]} \ \),極数\( \ p=6 \ \)であるから,ワンポイント解説「1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)」の通り,
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120\times 60}{6} \\[ 5pt ]
&=&1 \ 200 \ \mathrm {[{min}^{-1}]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,滑り\( \ s \ \)は,回転速度が\( \ N=1 \ 170 \ \mathrm {[{min}^{-1}]} \ \)であるから,ワンポイント解説「2.誘導機の滑り\( \ s \ \)」の通り,
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ]
&=&\frac {1 \ 200-1 \ 170}{1 \ 200} \\[ 5pt ]
&=&0.025 \\[ 5pt ]
\end{eqnarray}
\]
となる。問題文より,二次抵抗値が一定のとき,滑りとトルクは比例するので,定格負荷の\( \ 80 \ \mathrm {%} \ \)のトルクで運転する場合の滑り\( \ s^{\prime } \ \)は,
\[
\begin{eqnarray}
s^{\prime } &=&0.8s \\[ 5pt ]
&=&0.8\times 0.025 \\[ 5pt ]
&=&0.02 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(3)
ワンポイント解説「4.巻線形誘導電動機のトルクの比例推移」の通り,トルクが一定であるとき滑りは二次巻線回路の抵抗値に比例するので,二次巻線端子に抵抗器を接続したときの滑り\( \ s^{\prime \prime } \ \)は,
\[
\begin{eqnarray}
s^{\prime \prime } &=&\frac {2.5r_{2}^{\prime }}{r_{2}^{\prime }}s^{\prime } \\[ 5pt ]
&=&2.5\times 0.02 \\[ 5pt ]
&=&0.05 \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,回転速度\( \ N^{\prime } \ \mathrm {[{min}^{-1}]} \ \)は,ワンポイント解説「2.誘導機の滑り\( \ s \ \)」の通り,
\[
\begin{eqnarray}
N^{\prime }&=&\left( 1-s^{\prime \prime } \right) N_{\mathrm {s}} \\[ 5pt ]
&=&\left( 1-0.05 \right) \times 1 \ 200 \\[ 5pt ]
&=&1 \ 140 \ \mathrm {[{min}^{-1}]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは