《理論》〈電子理論〉[R06下:問13]トランジスタの静特性を利用した回路演算に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

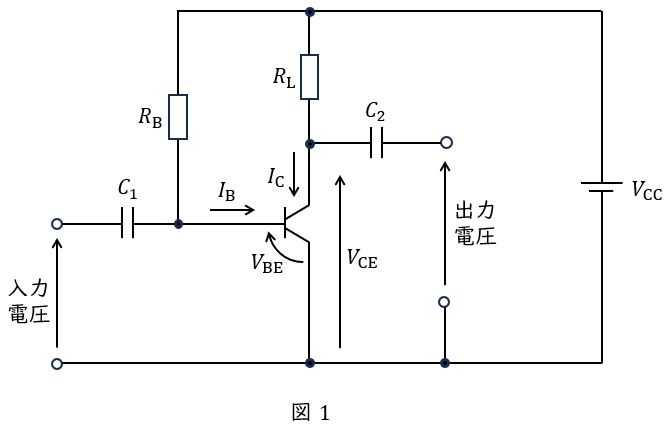
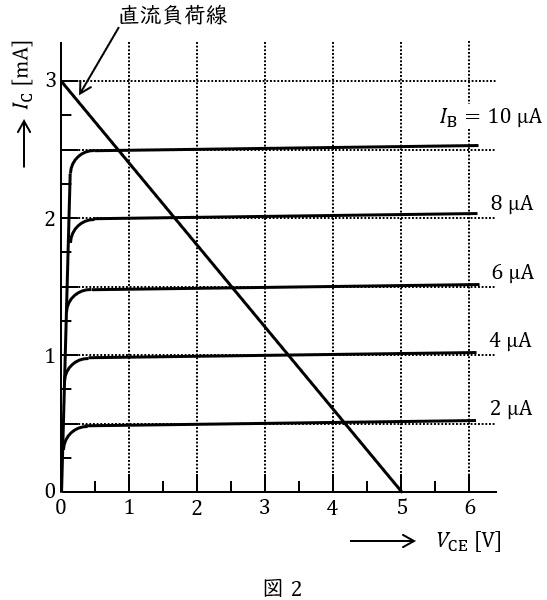
図1は，固定バイアス回路を用いた，\( \ R_{\mathrm {B}} \ \)の値が未知のエミッタ接地トランジスタ増幅回路である。図2は，この増幅回路で用いているトランジスタのコレクタ－エミッタ間電圧\( \ V_{\mathrm {CE}} \ \)とコレクタ電流\( \ I_{\mathrm {C}} \ \)との関係を予め調べ示した静特性である。ただし，五つのベース電流の値\( \ I_{\mathrm {B}} \ \mathrm {[\mu A]} \ \)のみに対する曲線であり，増幅回路の負荷抵抗\( \ R_{\mathrm {L}} \ \)の負荷線も重ねて示している。今，増幅回路の動作点を測定したところ\( \ V_{\mathrm {CE}}=3.0 \ \mathrm {V} \ \)であった。抵抗\( \ R_{\mathrm {B}} \ \)の値\( \ \mathrm {[M\Omega ]} \ \)として最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，ベース－エミッタ間電圧\( \ V_{\mathrm {BE}} \ \)を\( \ 0.7 \ \mathrm {V} \ \)としてよい。なお，\( \ C_{\mathrm {1}} \ \)，\( \ C_{\mathrm {2}} \ \)は結合コンデンサであり，\( \ V_{\mathrm {CC}} \ \)は直流電圧源である。

　(1)　\( \ 0.5 \ \)　　(2)　\( \ 0.9 \ \)　　(3)　\( \ 1.5 \ \)　　(4)　\( \ 3.0 \ \)　　(5)　\( \ 6.0 \ \)

【ワンポイント解説】

トランジスタの静特性を利用した回路演算に関する問題です。
基本的な電気回路の知識以外の特別な知識は必要としない問題ですが，この問題に特化した解法を要する問題であるため，正答率は低かったと予想されます。また，\( \ \mathrm {CBT} \ \)試験で出題されたら，かなり厳しい問題と言えるでしょう。
ただし，平成29年問13に類題が出題されていましたので，過去問演習を十分にされていた方は解けた可能性があります。

【解答】

解答：(2)
図1-1に示す閉回路について，キルヒホッフの法則を適用すると，
\[
\begin{eqnarray}
V_{\mathrm {CC}}&=&V_{\mathrm {CE}}+R_{\mathrm {L}}I_{\mathrm {C}} \\[ 5pt ] \end{eqnarray}
\] となり，図2の直流負荷線より，\( \ I_{\mathrm {C}}=0 \ \mathrm {[mA]} \ \)のとき\( \ V_{\mathrm {CE}}=5.0 \ \mathrm {[V]} \ \)であるから，
\[
\begin{eqnarray}
V_{\mathrm {CC}}&=&5+R_{\mathrm {L}}\times 0 \\[ 5pt ] &=&5 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。

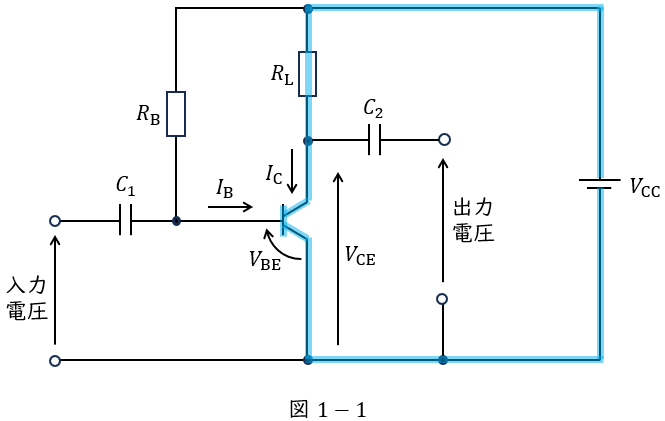
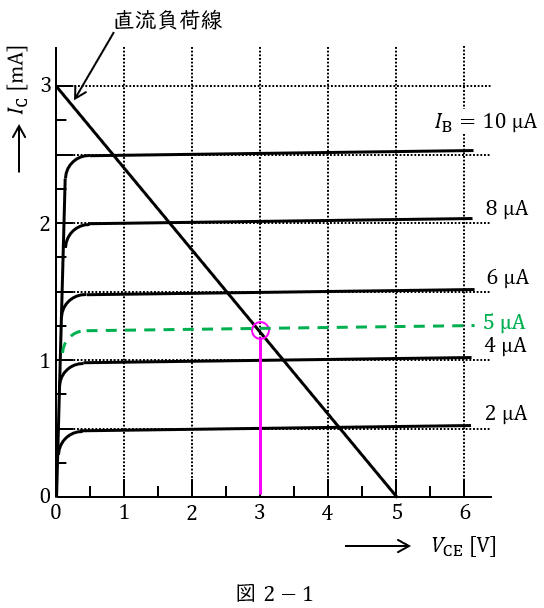
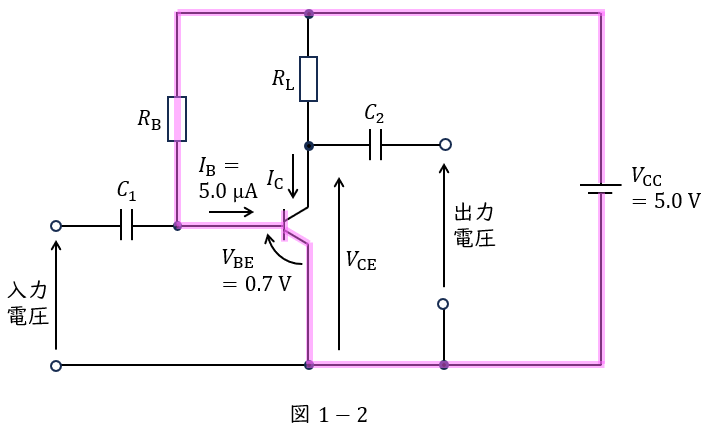
次に増幅回路の動作点を考えると，図2-1に示すように，\( \ V_{\mathrm {CE}}=3.0 \ \mathrm {[V]} \ \)のとき\( \ I_{\mathrm {B}}≒5.0 \ \mathrm {[\mu A]} \ \)となることがわかるので，図1-2に示す閉回路にキルヒホッフの法則を適用すると，
\[
\begin{eqnarray}
V_{\mathrm {CC}}&=&R_{\mathrm {B}}I_{\mathrm {B}}+V_{\mathrm {BE}} \\[ 5pt ] 5&=&R_{\mathrm {B}}\times 5.0\times 10^{-6}+0.7 \\[ 5pt ] R_{\mathrm {B}}\times 5.0\times 10^{-6}&=&4.3 \\[ 5pt ] R_{\mathrm {B}}&=&0.86\times 10^{6} \ \mathrm {[\Omega ]}　→　0.86 \ \mathrm {[M\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。