《機械》〈電気機器〉[H19:問12]電気的に温度を測定する温度計に関する空欄穴埋問題

【問題】

【難易度】★★★☆☆（普通）

電気的に温度を測定する方法には，熱電温度計，抵抗温度計など接触式のものと，放射温度計（全放射温度計，赤外線温度計）や光高温計など放射を利用した非接触式のものがある。

熱電温度計は，\( \ \fbox {　 （ア） 　} \ \)の熱起電力が熱接点と冷接点間の温度差に応じて生じるという\( \ \fbox {　 （イ） 　} \ \)効果を利用したものである。普通，温度差と熱起電力が直線的関係にある範囲で使用される。

抵抗温度計は，白金や銅，ニッケルなどの純粋な金属や\( \ \fbox {　 （ウ） 　} \ \)のような半導体の抵抗率が温度によって規則的に変化する特性を利用したものである。

全放射温度計は，「放射体から単位時間に放射される全放射エネルギーは放射体の絶対温度の\( \ \fbox {　 （エ） 　} \ \)に比例する」というステファン・ボルツマンの法則を応用したもので，光学系を使用して被測温体からの全放射エネルギーを受熱板に集めて，その温度上昇を熱電温度計などによって測定するものである。

赤外線温度計は，波長\( \ 700～20 \ 000 \ \mathrm {[nm]} \ \)程度の赤外放射を利用したもので，検出素子としては\( \ \fbox {　 （ウ） 　} \ \)などを使ったものと，\( \ \mathrm {HgCdTe} \ \)，\( \ \mathrm {InGaAs} \ \)，\( \ \mathrm {PbS} \ \)などの\( \ \fbox {　 （オ） 　} \ \)を使ったものがある。

上記の記述中の空白箇所(ア)，(イ)，(ウ)，(エ)及び(オ)に当てはまる語句として，正しいものを組み合わせたのは次のうちどれか。
\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） & （オ） \\
\hline
(1) & 　熱電対　　　 & 　ゼーベック　 & 　サーミスタ　 & 　4　乗　 & 　光電素子　 \\
\hline
(2) & 　サーミスタ　 & 　ペルチェ　　 & 　バイメタル　 & 　3　乗　 & 　光電素子　 \\
\hline
(3) & 　熱電対　　　 & 　ゼーベック　 & 　サーミスタ　 & 　3　乗　 & 　熱電素子　 \\
\hline
(4) & 　熱電対　　　 & 　ペルチェ　　 & 　バイメタル　 & 　4　乗　 & 　光電素子　 \\
\hline
(5) & 　サーミスタ　 & 　ゼーベック　 & 　バイメタル　 & 　4　乗　 & 　熱電素子　 \\
\hline
\end{array}
\]

【ワンポイント解説】

電気的に温度を測定する温度計に関する問題です。
電験での出題としては温度計自体の出題ではなく，その元の原理となる物理現象が出題されやすいです。出題頻度はそれほど高くありませんが，理論科目でも出題される可能性がある分野です。

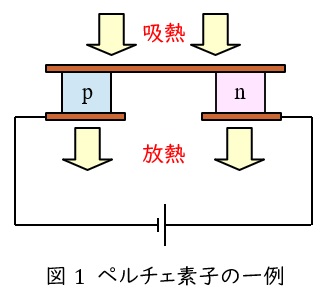
1.ペルチェ効果
異なる金属や半導体を接合して，電圧を加えると，吸熱もしくは発熱を発生する現象です。図1が代表的な半導体を使用したペルチェ素子で，電流の向きを逆にすると，発熱と吸熱も入れ替わります。

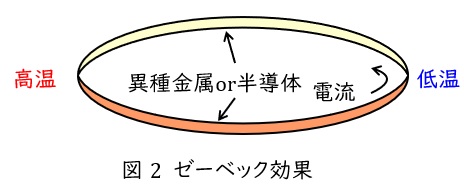
2.ゼーベック効果
異なる金属や半導体を図2のように接合して閉回路を作り，一端を高温（温接点），もう一端を低温（冷接点）とすると，熱起電力が発生し電流が流れる現象を言います。

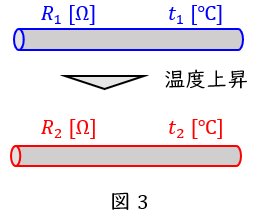
3.抵抗温度係数
白金，銅，ニッケル等の金属やサーミスタ等の半導体は一般に温度が変化すると抵抗値が変化する特性があり，その関係を示す係数を抵抗温度係数といいます。
例えば金属においては温度が高くなると一般に抵抗値は上昇し，基準温度\( \ t_{1} \ \mathrm {[℃]} \ \)における抵抗値が\( \ R_{1} \ \mathrm {[\Omega ]} \ \)，抵抗温度係数が\( \ \alpha \ \mathrm {[℃^{-1}]} \ \)の抵抗器があるとき，温度\( \ t_{2} \ \mathrm {[℃]} \ \)における抵抗値\( \ R_{2} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R_{2}&=&R_{1}\left\{ 1+\alpha \left( t_{2}-t_{1}\right) \right\} \\[ 5pt ] \end{eqnarray}
\] で求められます。（半導体の場合は温度が高くなると抵抗値は小さくなり，式はもう少し複雑です。）

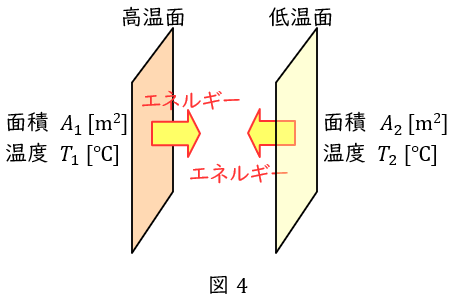
4.ステファン・ボルツマンの法則
図4のように，面積\( \ A_{1} \ \mathrm {[m^{2}]} \ \)，温度\( \ T_{1} \ \mathrm {[K]} \ \)の高温面と，面積\( \ A_{2} \ \mathrm {[m^{2}]} \ \)，温度\( \ T_{2} \ \mathrm {[K]} \ \)の低温面があるとき，\( \ 1 \ \)秒当たりに高温面から低温面に伝わるエネルギー\( \ \mathit {\Phi } \ \mathrm {[W]} \ \)は，\( \ \varepsilon \ \)を放射率，\( \ \sigma \ \mathrm {[W / \left( m^{2}\cdot K^{4}\right) ]} \ \)をステファン・ボルツマン定数，\( \ F_{12} \ \)を形態係数とすると，
\[
\begin{eqnarray}
\mathit {\Phi } &=& \varepsilon \sigma A_{1}F_{12}\left( T_{1}^{4}-T_{2}^{4}\right) \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

解答：(1)
(ア)
\( \ 2 \ \)種類の異なる金属を接合する温度センサを熱電対といいます。

(イ)
ワンポイント解説「2.ゼーベック効果」の通り，熱起電力が熱接点と冷接点間の温度差に応じて生じるという現象をゼーベック効果といいます。

(ウ)
ワンポイント解説「3.抵抗温度係数」の通り，サーミスタのような半導体は抵抗率が温度によって規則的に変化する特性があります。

(エ)
ワンポイント解説「4.ステファン・ボルツマンの法則」の通り，放射体から単位時間に放射される全放射エネルギーは放射体の絶対温度の\( \ 4 \ \)乗に比例します。

(オ)
赤外線温度計は物体が放射する赤外線が温度が上昇する程大きくなる性質を利用し温度を測定する機器で，検出素子としてはサーミスタなどを使ったものと，\( \ \mathrm {HgCdTe} \ \)，\( \ \mathrm {InGaAs} \ \)，\( \ \mathrm {PbS} \ \)などの光電素子を使ったものがあります。光電素子は光エネルギーを電気エネルギーに変換する素子です。