《理論》〈電子理論〉[R07上:問11]ホール素子の動作原理に関する空欄穴埋問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，図1及び図2に示す原理図を用いてホール素子の動作原理について述べたものである。

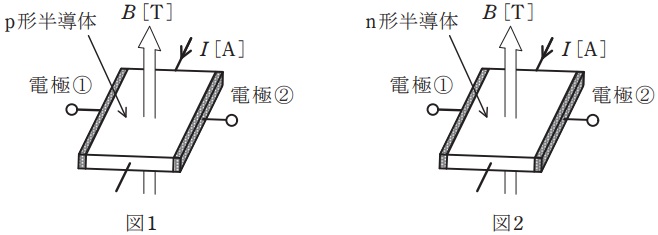
図1に示すように，\( \ \mathrm {p} \ \)形半導体に直流電流\( \ I \ \mathrm {[A]} \ \)を流し，半導体の表面に対して垂直に下から上向きに磁束密度\( \ B \ \mathrm {[T]} \ \)の平等磁界を半導体に加えると，半導体内の正孔は進路を曲げられ，電極①には\( \ \fbox {　 （ア） 　} \ \)電荷，電極②には\( \ \fbox {　 （イ） 　} \ \)電荷が分布し，半導体の内部に電界が生じる。 また，図2の\( \ \mathrm {n} \ \)形半導体の場合は，電界の向きは\( \ \mathrm {p} \ \)形半導体の場合と\( \ \fbox {　 （ウ） 　} \ \)である。この電界により，電極①－②間にホール電圧\( \ V_{\mathrm {H}} \ \mathrm {[V]} \ \)が発生し，それは直流電流\( \ I \ \mathrm {[A]} \ \)にほぼ\( \ \fbox {　 （エ） 　} \ \)する。

上記の記述中の空白箇所(ア)～(エ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） \\
\hline
(1) & 　負　 & 　正　 & 　同じ　 & 　反比例　 \\
\hline
(2) & 　正　 & 　負　 & 　同じ　 & 　反比例　 \\
\hline
(3) & 　負　 & 　正　 & 　同じ　 & 　比例　 \\
\hline
(4) & 　正　 & 　負　 & 　反対　 & 　比例　 \\
\hline
(5) & 　負　 & 　正　 & 　反対　 & 　比例　 \\
\hline
\end{array}
\]

【ワンポイント解説】

ホール効果の原理を問う問題です。
ホール効果の定量的な原理は\( \ 2 \ \)種レベル以上の内容となるので，概要を理解しておけば良いかと思います。
本問は令和5年上期問11や平成22年問11の類題となります。

1.電界\( \ E \ \mathrm {[V / m]} \ \)により電荷\( \ q \ \mathrm {[C]} \ \)に働く力\( \ F \ \mathrm {[N]} \ \)の大きさ
一様な電界\( \ E \ \mathrm {[V / m]} \ \)が電荷\( \ q \ \mathrm {[C]} \ \)にかかっているとき，この電荷\( \ q \ \)に働く力の大きさ\( \ F \ \mathrm {[N]} \ \)は，
\[
\begin{eqnarray}
F &=&qE \\[ 5pt ] \end{eqnarray}
\] となります。

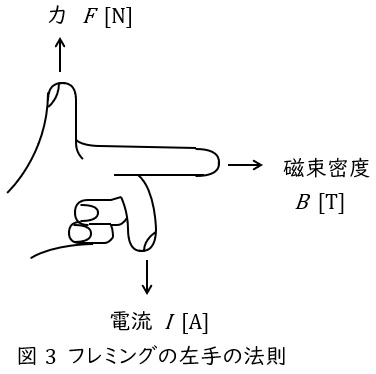
2.フレミングの左手の法則
中指を電流の向き，人差し指を磁界の向きに合わせると，親指の方向に力が働くという法則で，頭文字を取って「電磁力」と覚えます。
磁束密度の大きさ\( \ B \ \mathrm {[T]} \ \)，電流の大きさ\( \ I \ \mathrm {[A]} \ \)，直線状導体の長さを\( \ l \ \mathrm {[m]} \ \)とすると，導体に発生する電磁力\( \ F \ \mathrm {[N]} \ \)は，
\[
\begin{eqnarray}
F &=&BIl \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(4)
(ア)
ワンポイント解説「2.フレミングの左手の法則」の通り，左手を開いて電流の方向を中指（奥から手前），磁束密度の方向を人差し指（下から上）とすると，親指は電極②→①方向になるため，多数キャリヤである正孔は①側に移動します。
したがって，電極①には正電荷が分布します。

(イ)
（ア）より電極①に正電荷が分布するので，電極②には反対の極性である負電荷が分布します。

(ウ)
フレミングの左手の法則の原理は全く同じですが，\( \ \mathrm {n} \ \)形半導体の場合は電子が多数キャリヤなので，電子が電極①側に移動し，①に負電荷が分布，②に反対の極性である正電荷が分布します。したがって，電界の方向は\( \ \mathrm {p} \ \)形半導体と反対方向となります。

(エ)
正孔の電荷量が\( \ q \ \mathrm {[C]} \ \)，正孔の濃度が\( \ p \ \mathrm {[1 /m^{3}]} \ \)であるとすると，ホール電圧\( \ V_{\mathrm {H}} \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {H}} &=&\frac {BI}{qpd} \\[ 5pt ] \end{eqnarray}
\] で求められ，直流電流\( \ I \ \mathrm {[A]} \ \)にほぼ比例します。電流が大きいほどキャリヤの移動が大きくなることがイメージできれば良いかと思います。

※導出過程を理解したい場合には電験王ＨＰ1種令和3年理論科目問6を参照して下さい。