《理論》〈電気回路〉[H18:問9]抵抗とインダクタンスを直列した回路の位相に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

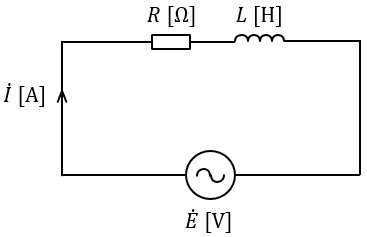
図のように，\( \ R \ \mathrm {[\Omega ]} \ \)の抵抗とインダクタンス\( \ L \ \mathrm {[H]} \ \)のコイルを直列に接続した回路がある。この回路に角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)の正弦波交流電圧\( \ \dot E \ \mathrm {[V]} \ \)を加えたとき，この電圧の位相\( \ \mathrm {[rad]} \ \)に対して回路を流れる電流\( \ \dot I \ \mathrm {[A]} \ \)の位相\( \ \mathrm {[rad]} \ \)として，正しいのは次のうちどれか。

(1)　\( \ \displaystyle \sin ^{-1} \frac {R}{\omega L} \ \mathrm {[rad]} \ \)進む

(2)　\( \ \displaystyle \cos ^{-1} \frac {R}{\omega L} \ \mathrm {[rad]} \ \)遅れる

(3)　\( \ \displaystyle \cos ^{-1} \frac {\omega L}{R} \ \mathrm {[rad]} \ \)進む

(4)　\( \ \displaystyle \tan ^{-1} \frac {R}{\omega L} \ \mathrm {[rad]} \ \)遅れる

(5)　\( \ \displaystyle \tan ^{-1} \frac {\omega L}{R} \ \mathrm {[rad]} \ \)遅れる

【ワンポイント解説】

\( \ RL \ \)直列回路の電圧と電流の関係を考える問題です。
実際に回路のベクトル図を描くとイメージがしやすく間違いが減るかと思います。
インダクタンスが遅れであることは交流回路の基本となりますので，(1)と(3)だけは選ばないように注意しましょう。

1.抵抗，コイル，コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係
抵抗\( \ R \ \mathrm {[\Omega ]} \ \)，コイル\( \ L \ \mathrm {[H]} \ \)，コンデンサ\( \ C \ \mathrm {[F]} \ \)があり，電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)及び周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき，それぞれのインピーダンスは，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ] {\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ] {\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}
\] で求められ，それぞれの電圧と電流の関係は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ] {\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ] {\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ] \end{eqnarray}
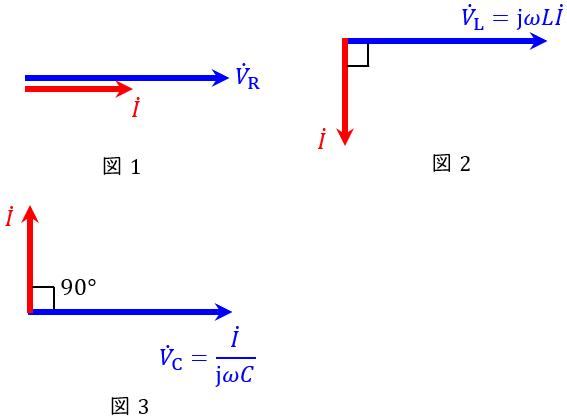
\] となります。この関係をベクトル図に表すと，図1～図3となります。

【解答】

解答：(5)
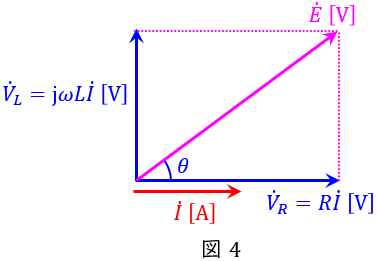
抵抗\( \ R \ \mathrm {[\Omega ]} \ \)に加わる電圧を\( \ \dot V_{R} \ \mathrm {[V]} \ \)，インダクタンス\( \ L \ \mathrm {[H]} \ \)に加わる電圧を\( \ \dot V_{L} \ \mathrm {[V]} \ \)とし，電流\( \ \dot I \ \mathrm {[A]} \ \)を基準にベクトル図を描くと，図4のようになる。

図4より，電流\( \ \dot I \ \mathrm {[A]} \ \)は電圧\( \ \dot E \ \mathrm {[V]} \ \)に対し遅れであり，その位相\( \ \theta \ \mathrm {[rad]} \ \)は，
\[
\begin{eqnarray}
\tan \theta &=&\frac {\omega LI}{RI} \\[ 5pt ] &=&\frac {\omega L}{R} \\[ 5pt ] \theta &=&\tan ^{-1}\frac {\omega L}{R} \\[ 5pt ] \end{eqnarray}
\] と求められる。