《機械》〈情報伝送及び処理〉[H30:問14]論理回路の真理値表の導出に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

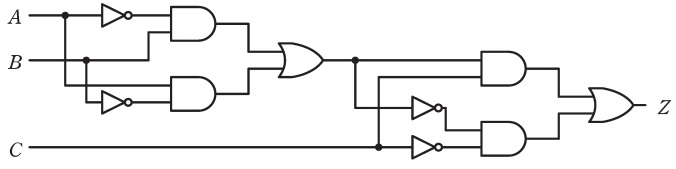
図のように，入力信号\(A\)，\(B\)及び\(C\)，出力信号\(Z\)の論理回路がある。この論理回路には排他的論理和(EX-OR)を構成する部分と排他的否定論理和(EX-NOR)を構成する部分が含まれている。

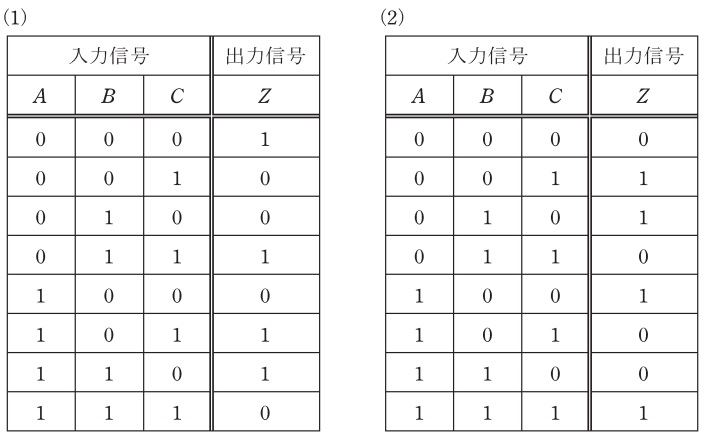
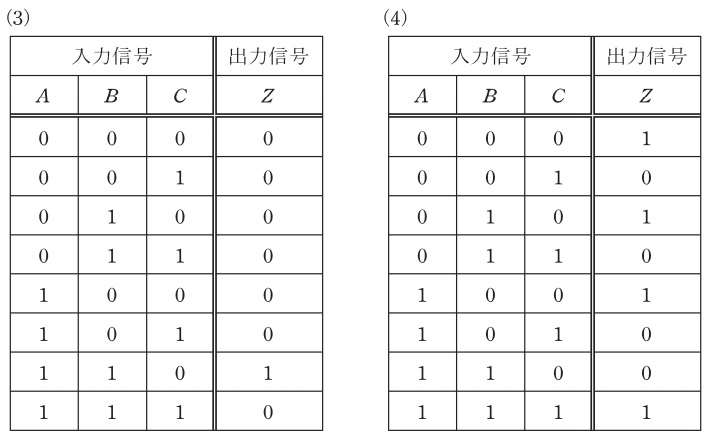
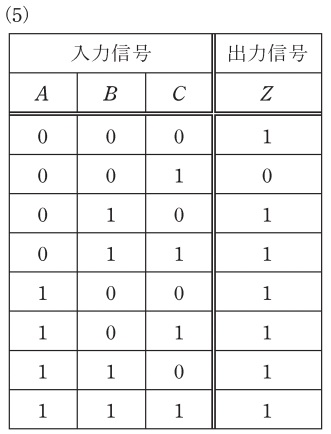
この論理回路の真理値表として，正しいものを次の(1)～(5)のうちから一つ選べ。

【ワンポイント解説】

本問のような問題はいろいろな解き方があります。信号に一つ一つ\(0\)や\(1\)を入れて出力がどうなるかを求めたり，論理式を整理して求めたりする方法があると思いますが各々が得意な方法で解けば良いと思います。本問では論理式を用いた方法で解いてみたいと思います。

1.ド・モルガンの法則
\(A\)と\(B\)の論理積(AND)を\(A\cdot B\)，論理和(OR)を\(A+B\)，\(A\)の否定(NOT)を\(\overline A\)とすると，
\[
\begin{eqnarray}
\overline {A\cdot B} &=&\overline A +\overline B \\[ 5pt ] \overline {A+ B} &=&\overline A \cdot \overline B \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(1)
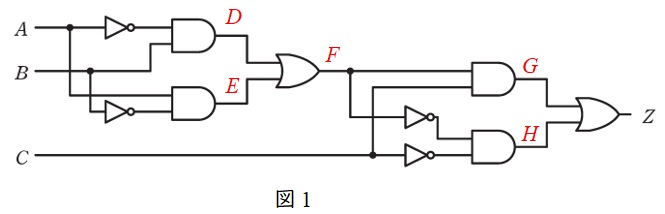
問題図の各部の信号を図1のようにする。\(D=\overline A \cdot B\)，\(E=A \cdot \overline B\)であるから，
\[
\begin{eqnarray}
F &=&D+E \\[ 5pt ] &=&\overline A \cdot B +A \cdot \overline B \\[ 5pt ] \end{eqnarray}
\] となる。\(G= F \cdot C\)，\(H=\overline F \cdot \overline C\)であるから，
\[
\begin{eqnarray}
Z &=&G+H \\[ 5pt ] &=&F \cdot C +\overline F \cdot \overline C \\[ 5pt ] &=&\left( \overline A \cdot B +A \cdot \overline B\right) \cdot C +\left( \overline {\overline A \cdot B +A \cdot \overline B} \right) \cdot \overline C \\[ 5pt ] &=& \overline A \cdot B \cdot C +A \cdot \overline B \cdot C +\left( \overline {\overline A \cdot B}\cdot \overline {A \cdot \overline B}\right) \cdot \overline C \\[ 5pt ] &=& \overline A \cdot B \cdot C +A \cdot \overline B \cdot C +\left[ \left( \overline {\overline A}+\overline B\right) \cdot \left( \overline A +\overline {\overline B}\right) \right] \cdot \overline C \\[ 5pt ] &=& \overline A \cdot B \cdot C +A \cdot \overline B \cdot C +\left[ \left( A+\overline B\right) \cdot \left( \overline A +B\right) \right] \cdot \overline C \\[ 5pt ] &=& \overline A \cdot B \cdot C +A \cdot \overline B \cdot C +\left( A\cdot \overline A +A\cdot B+ \overline A\cdot \overline B +B\cdot \overline B\right) \cdot \overline C \\[ 5pt ] &=& \overline A \cdot B \cdot C +A \cdot \overline B \cdot C +\left( A\cdot B+ \overline A\cdot \overline B \right) \cdot \overline C \\[ 5pt ] &=& \overline A \cdot B \cdot C +A \cdot \overline B \cdot C +A\cdot B\cdot \overline C+ \overline A\cdot \overline B\cdot \overline C \\[ 5pt ] \end{eqnarray}
\] となるので，これを表す真理値表は(1)となる。