【問題】
【難易度】★★★☆☆(普通)
支持点間が\( \ 180 \ \mathrm {m} \ \),たるみが\( \ 3.0 \ \mathrm {m} \ \)の架空電線路がある。
いま架空電線路の支持点間を\( \ 200 \ \mathrm {m} \ \)にしたとき,たるみを\( \ 4.0 \ \mathrm {m} \ \)にしたい。電線の最低点における水平張力をもとの何\( \ \left[ %\right] \ \)にすればよいか。最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,支持点間の高低差はなく,電線の単位長当たりの荷重は変わらないものとし,その他の条件は無視するものとする。
(1) \(83.3\) (2) \(92.6\) (3) \(108.0\) (4) \(120.0\) (5) \(148.1\)
【ワンポイント解説】
電線のたるみの問題は頻出の問題で,公式は積分を使えば導出することができますが,三種の試験では丸暗記すれば大丈夫です。
1.電線のたるみの公式
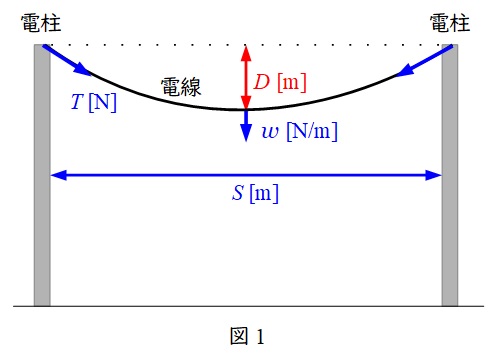
図1の通り,径間を\( \ S \ [ \mathrm {m} ] \ \),水平張力\( \ T \ [ \mathrm {N} ] \ \),電線1mあたりの質量荷重\( \ w \ [ \mathrm {N/m} ] \ \)とすると,電線のたるみ\( \ D \ [\mathrm {m} ] \ \)は,
\[
\begin{eqnarray}
D&=&\frac {wS^{2}}{8T} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【関連する「電気の神髄」記事】
【解答】
解答:(2)
支持点間が\( \ 180 \ \mathrm {m} \ \),たるみが\( \ 3.0 \ \mathrm {m} \ \)の時の水平張力を\( \ T_{1} \ \),支持点間を\( \ 200 \ \mathrm {m} \ \),たるみが\( \ 4.0 \ \mathrm {m} \ \)の時の水平張力を\( \ T_{2} \ \)とすると,
\[
\begin{eqnarray}
\frac {w\cdot 180^{2}}{8T_{1}}&=&3 &・・・①& \\[ 5pt ]
\frac {w\cdot 200^{2}}{8T_{2}}&=&4 &・・・②& \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,①÷②を計算すると,
\[
\begin{eqnarray}
\frac {180^{2}\cdot T_{2}}{200^{2}\cdot T_{1}} &=& \frac {3}{4} \\[ 5pt ]
\frac {T_{2}}{T_{1}} &=& \frac {3\times 200^{2}}{4\times 180^{2}} \\[ 5pt ]
\frac {T_{2}}{T_{1}} &≒& 0.926
\end{eqnarray}
\]
となり,\( \ 92.6 \ % \ \)と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは