《理論》〈電磁気〉[R01:問3]ヒステリシスループに関する空欄穴埋問題

【問題】

【難易度】★★★☆☆（普通）

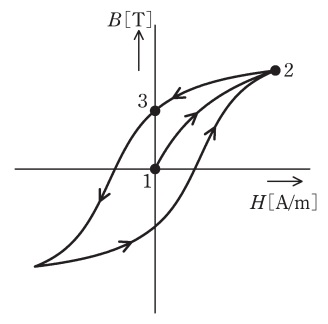
図は積層した電磁鋼板の鉄心の磁化特性(ヒステリシスループ)を示す。図中の\( \ B \ \mathrm {[T]} \ \)及び\( \ H \ \mathrm {[A／m]} \ \)はそれぞれ磁束密度及び磁界の強さを表す。この鉄心にコイルを巻きリアクトルを製作し，商用交流電源に接続した。実効値が\( \ V \ \mathrm {[V]} \ \)の電源電圧を印加すると図中に矢印で示す軌跡が確認された。コイル電流が最大のときの点は\( \ \fbox {　 （ア） 　} \ \)である。次に，電源電圧実効値が一定に保たれたまま，周波数がやや低下したとき，ヒステリシスループの面積は\( \ \fbox {　 （イ） 　} \ \)。一方，周波数が一定で，電源電圧実効値が低下したとき，ヒステリシスループの面積は\( \ \fbox {　 （ウ） 　} \ \)。最後に，コイル電流実効値が一定で，周波数がやや低下したとき，ヒステリシスループの面積は\( \ \fbox {　 （エ） 　} \ \)。

上記の記述中の空白箇所(ア)，(イ)，(ウ)及び(エ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） \\
\hline
(1) & 1 & 大きくなる & 小さくなる & 大きくなる \\
\hline
(2) & 2 & 大きくなる & 小さくなる & あまり変わらない \\
\hline
(3) & 3 & あまり変わらない & あまり変わらない & 小さくなる \\
\hline
(4) & 2 & 小さくなる & 大きくなる & あまり変わらない \\
\hline
(5) & 1 & 小さくなる & 大きくなる & あまり変わらない \\
\hline
\end{array}
\]

【ワンポイント解説】

ヒステリシスループの問題は計算問題が出題されない分野です。真空中では\( \ B=\mu _{0}H \ \)の関係が成立するとしていますが，磁性体ではこの関係は成立せず，磁界中で磁気を帯び磁化されます。磁化されることによって，ヒステリシスループで囲まれた面積に比例したヒステリシス損が発生します。本問の(ア)は確実に理解しておきたい内容となります。

1.リアクトルのリアクタンス\( \ X_{\mathrm {L}} \ \)
インダクタンスが\( \ L \ \mathrm {[H]} \ \)のリアクトル(コイル)のリアクタンス\( \ X_{\mathrm {L}} \ \mathrm {[\Omega ]} \ \)は，周波数を\( \ f \ \mathrm {[Hz]} \ \)，角周波数を\( \ \omega \ \mathrm {[rad／s]}\ \)とすると，
\[
\begin{eqnarray}
X_{\mathrm {L}} &=&\mathrm {j}\omega L \ \mathrm {[\Omega ]} \\[ 5pt ] &=&\mathrm {j}2\pi f L \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(2)
(ア)
磁界の強さ\( \ H \ \)は電流\( \ I \ \)に比例し，磁束密度\( \ B \ \)は磁界の強さ\( \ H \ \)に比例します。したがって，磁束密度\( \ B \ \)は電流\( \ I \ \)に比例するので，コイル電流が最大となるのは磁束密度及び磁界の強さが最大となる点\( \ 2 \ \)となります。

(イ)
ワンポイント解説「1.リアクトルのリアクタンス\( \ X_{\mathrm {L}} \ \)」の通り，周波数が低下するとコイルのリアクタンスが低下するので，コイル電流が増加し，磁界の強さ\( \ H \ \)及び磁束密度\( \ B \ \)が大きくなります。したがって，ヒステリシスループの面積は大きくなります。

(ウ)
周波数が変わらないので，リアクタンスの大きさが変わりません。この状況で電源電圧が低下すると，オームの法則によりコイル電流は減少します。コイル電流が減少すると，磁界の強さ\( \ H \ \)及び磁束密度\( \ B \ \)は小さくなります。したがって，ヒステリシスループの面積は小さくなります。

(エ)
コイル電流が変わらなければ，磁界の強さ\( \ H \ \)及び磁束密度\( \ B \ \)はあまり変わりません。したがって，ヒステリシスループの面積はあまり変わりません。