《理論》〈電気回路〉[H25:問8]複雑な直並列回路に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

図に示すような抵抗の直並列回路がある。この回路に直流電圧\( \ 5 \ \mathrm {[V]} \ \)を加えたとき，電源から流れ出る電流\( \ I \ \mathrm {[A]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

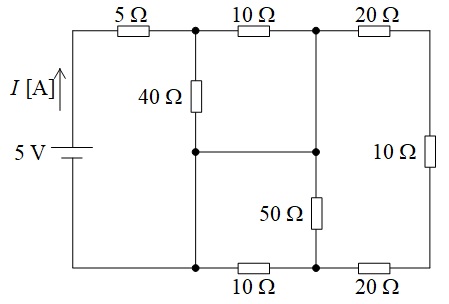
　(1)　\(0.2\)　　(2)　\(0.4\)　　(3)　\(0.6\)　　(4)　\(0.8\)　　(5)　\(1.0\)

【ワンポイント解説】

電験としては一風変わった問題と言えます。難しい公式や計算は必要ありませんが，あれ？と気付くかどうかが勝負になり，いざ本番になるとなかなか気付けなくなります。過去問をできるだけ多く解き，「これだけ複雑な回路だと単純に合成抵抗を求める問題ではないな」とピンとくるようになることが大事であると思います。

1.合成抵抗
抵抗\( \ R_{1} \ \)と\( \ R_{2} \ \)が与えられている時，それぞれの合成抵抗\( \ R \ \)は以下の式で与えられます。

①直列
直列合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

②並列
並列合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，整理すると，
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(2)
図1に示すように，赤囲みの部分が短絡されているため，赤囲みの部分は同電位となり，その右側には電流は流れない。したがって，右部分の回路は無視でき，図2のように書き換えることができる。

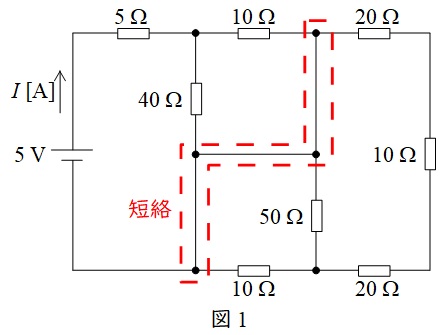
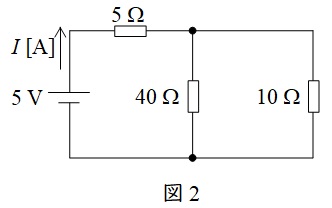
図2より，回路の合成抵抗\( \ R \ \)は，
\[
\begin{eqnarray}
R&=&5+\frac {40\times 10}{40+10} \\[ 5pt ] &=&5+8 \\[ 5pt ] &=&13 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となるから，回路に流れる電流\( \ I \ \)は，
\[
\begin{eqnarray}
I&=&\frac {5}{13} \\[ 5pt ] &≒&0.385　→　0.4 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。