《理論》〈電気回路〉[R05:問3]直流回路における等価回路への変換に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

次の文章は直流回路の等価回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

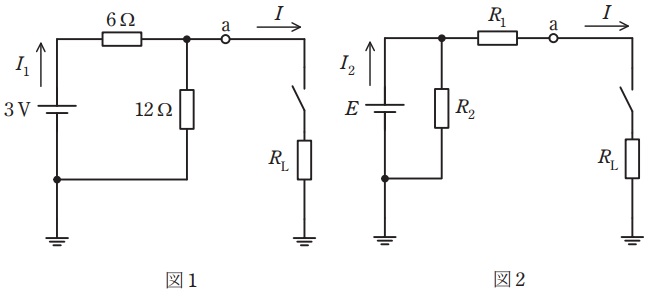
図1に示す直流電圧源と抵抗とスイッチからなる回路を考える。図2は，図1の等価回路である。

図1と図2の回路のスイッチを開いたとき，端子\( \ \mathrm {a} \ \)の電位は等しいので電源電圧\( \ E= \ \fbox {　 （１） 　} \ \)となる。端子\( \ \mathrm {a} \ \)と大地の間の抵抗も等しいので抵抗\( \ R_{1}= \ \fbox {　 （２） 　} \ \)となる。回路の消費電力が等しいので抵抗\( \ R_{2}= \ \fbox {　 （３） 　} \ \)となる。

次に，図1と図2の回路のスイッチを閉じて回路に同じ負荷抵抗\( \ R_{\mathrm {L}} \ \)を接続すると，\( \ R_{\mathrm {L}} \ \)を流れる電流\( \ I \ \)は同じ値となる。このとき，図1の直流電圧源を流れる電流\( \ I_{1} \ \)と，図2の直流電圧源を流れる電流\( \ I_{2} \ \)を求めると，\( \ I_{1}= \ \fbox {　 （４） 　} \ \)，\( \ I_{2}= \ \fbox {　 （５） 　} \ \)となる。\( \ I_{1} \ \)と\( \ I_{2} \ \)の値から，負荷抵抗\( \ R_{\mathrm {L}} \ \)が同じなら図1と図2の回路が消費する電力は等しいことが分かる。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {1}{6}\times \frac {12+R_{\mathrm {L}}}{4+R_{\mathrm {L}}} \ \mathrm {[A]}　　　　　&（ロ）&　\frac {7}{4}\times \frac {6+R_{\mathrm {L}}}{4+R_{\mathrm {L}}} \ \mathrm {[A]}　　　　　&（ハ）&　\frac {5}{2}\times \frac {8+R_{\mathrm {L}}}{4+R_{\mathrm {L}}} \ \mathrm {[A]} \\[ 5pt ] &（ニ）&　\frac {5}{3}\times \frac {8+R_{\mathrm {L}}}{4+R_{\mathrm {L}}} \ \mathrm {[A]}　　　　　　　&（ホ）&　\frac {7}{6}\times \frac {6+R_{\mathrm {L}}}{4+R_{\mathrm {L}}} \ \mathrm {[A]}　　　　　&（ヘ）&　\frac {1}{4}\times \frac {12+R_{\mathrm {L}}}{4+R_{\mathrm {L}}} \ \mathrm {[A]} \\[ 5pt ] &（ト）&　7 \ \Omega　　　　　&（チ）&　2 \ \mathrm {V}　　　　　&（リ）&　5 \ \Omega \\[ 5pt ] &（ヌ）&　9 \ \Omega　　　　　&（ル）&　6 \ \mathrm {V}　　　　　&（ヲ）&　3 \ \Omega \\[ 5pt ] &（ワ）&　12 \ \mathrm {V}　　　　&（カ）&　4 \ \Omega 　　　　　&（ヨ）&　8 \ \Omega \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

直流回路における等価回路への変換に関する問題です。
\( \ 3 \ \)種の頃に学習した分圧・分流の法則，合成抵抗，等の回路演算を駆使すれば完答を狙える問題となります。合格のためにはできれば完答しておきたい問題です。

【解答】

(1)解答：チ
図1の回路において，スイッチを開いたとき，端子\( \ \mathrm {a} \ \)の電位\( \ V_{\mathrm {a}} \ \mathrm {[V]} \ \)は，分圧の法則より，
\[
\begin{eqnarray}
V_{\mathrm {a}} &=&\frac {12}{6+12}\times 3 \\[ 5pt ] &=&2 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となり，図2の回路において，スイッチを開いたとき，端子\( \ \mathrm {a} \ \)の電位は\( \ R_{1} \ \)に電流が流れないため\( \ V_{\mathrm {a}}=E \ \mathrm {[V]} \ \)となる。よって，図1と図2の回路のスイッチを開いたとき，端子\( \ \mathrm {a} \ \)の電位は等しいので，
\[
\begin{eqnarray}
E&=&V_{\mathrm {a}} \\[ 5pt ] &=&2 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：カ
図1において，電圧源を短絡し端子\( \ \mathrm {a} \ \)から電源側をみたときの抵抗\( \ R_{0} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R_{0}&=&\frac {12\times 6}{12+6} \\[ 5pt ] &=&4 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] であり，図2において，電圧源を短絡し端子\( \ \mathrm {a} \ \)から電源側をみたときの抵抗は\( \ R_{1} \ \mathrm {[\Omega ]} \ \)である。したがって，図1と図2の端子\( \ \mathrm {a} \ \)から電源側をみたときの抵抗は等しいので，
\[
\begin{eqnarray}
R_{1}&=&R_{0} \\[ 5pt ] &=&4 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ヨ
図1での消費電力\( \ P \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P&=&\frac {3^{2}}{6+12} \\[ 5pt ] &=&0.5 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] であり，これが図2の消費電力と等しいので，
\[
\begin{eqnarray}
P&=&\frac {E^{2}}{R_{2}} \\[ 5pt ] 0.5&=&\frac {2^{2}}{R_{2}} \\[ 5pt ] R_{2}&=&\frac {2^{2}}{0.5} \\[ 5pt ] &=&8 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：イ
図1の回路の合成抵抗\( \ R_{1}^{\prime } \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R_{1}^{\prime }&=&6+\frac {12R_{\mathrm {L}}}{12+R_{\mathrm {L}}} \\[ 5pt ] &=&\frac {6\left( 12+R_{\mathrm {L}}\right) +12R_{\mathrm {L}}}{12+R_{\mathrm {L}}} \\[ 5pt ] &=&\frac {72+18R_{\mathrm {L}}}{12+R_{\mathrm {L}}} \\[ 5pt ] &=&\frac {18\left( 4+R_{\mathrm {L}}\right) }{12+R_{\mathrm {L}}} \\[ 5pt ] \end{eqnarray}
\] であるから，直流電圧源を流れる電流\( \ I_{1} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{1}&=&\frac {3}{R_{1}^{\prime }} \\[ 5pt ] &=&\frac {3}{\displaystyle \frac {18\left( 4+R_{\mathrm {L}}\right) }{12+R_{\mathrm {L}}}} \\[ 5pt ] &=&\frac {3\left( 12+R_{\mathrm {L}}\right) }{18\left( 4+R_{\mathrm {L}}\right) } \\[ 5pt ] &=&\frac {12+R_{\mathrm {L}}}{6\left( 4+R_{\mathrm {L}}\right) } \\[ 5pt ] &=&\frac {1}{6}\times \frac {12+R_{\mathrm {L}}}{4+R_{\mathrm {L}}} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヘ
図2の回路の合成抵抗\( \ R_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R_{2}^{\prime }&=&\frac {R_{2}\left( R_{1}+R_{\mathrm {L}}\right) }{R_{2}+\left( R_{1}+R_{\mathrm {L}}\right) } \\[ 5pt ] &=&\frac {8\left( 4+R_{\mathrm {L}}\right) }{8+\left( 4+R_{\mathrm {L}}\right) } \\[ 5pt ] &=&\frac {8\left( 4+R_{\mathrm {L}}\right) }{12+R_{\mathrm {L}}} \\[ 5pt ] \end{eqnarray}
\] であるから，直流電圧源を流れる電流\( \ I_{2} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{2}&=&\frac {E}{R_{2}^{\prime }} \\[ 5pt ] &=&\frac {2}{\displaystyle \frac {8\left( 4+R_{\mathrm {L}}\right) }{12+R_{\mathrm {L}}}} \\[ 5pt ] &=&\frac {2\left( 12+R_{\mathrm {L}}\right) }{8\left( 4+R_{\mathrm {L}}\right) } \\[ 5pt ] &=&\frac {12+R_{\mathrm {L}}}{4\left( 4+R_{\mathrm {L}}\right) } \\[ 5pt ] &=&\frac {1}{4}\times \frac {12+R_{\mathrm {L}}}{4+R_{\mathrm {L}}} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。