《理論》〈電磁気〉[H21:問1]平行往復回路の外部自己インダクタンスに関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，$ \ 2 \ $本の導線より成る平行往復回路の外部自己インダクタンスに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる式又は語句を解答群の中から選び，その記号をマークシートに記入しなさい。なお，空気の透磁率を$ \ \mu _{0} \ $とする。

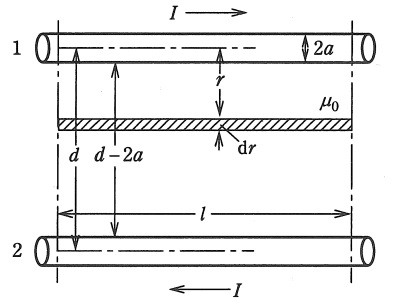
図のように，半径が$ \ a \ $で，無限に長い$ \ 2 \ $本の導線が線間距離$ \ d \ $を隔てて構成される一つの平行往復回路がある。ただし，$ \ a ≪d \ $とする。このとき，導線外部の磁束による自己インダクタンスは次のように求めることができる。

$ \ a ≪d \ $であるから，電流は導線の中心軸に集中しているとしてよい。したがって，導線$ \ 1 \ $の電流$ \ I \ $による導体外の磁界は，$ \ r \ $をその中心軸からの距離とすれば，$ \ r ＞a \ $として，$ \ \fbox {　（１）　} \ $となる。そこで，中心軸から$ \ r \ $のところにあって，幅が$ \ \mathrm {d}r \ $，長さが$ \ l \ $の帯状面積$ \ l\mathrm {d}r \ $を貫く磁束$ \ \mathrm {d}\phi \ $は$ \ \fbox {　（２）　} \ $となる。

平行往復回路の外部自己インダクタンスは$ \ 2 \ $本の導線間を通過している磁束から計算できる。したがって，導線$ \ 1 \ $の電流$ \ I \ $による長さ$ \ l \ $の部分に関係する外部磁束$ \ \mathit {\Phi } \ $は$ \ \mathrm {d}\phi \ $を$ \ r \ $について$ \ \fbox {　（３）　} \ $まで積分すれば，$ \ a ≪d \ $として$ \ \fbox {　（４）　} \ $となる。同じく導線$ \ 2 \ $の電流$ \ I \ $による長さ$ \ l \ $の部分に関係する外部磁束も$ \ \fbox {　（４）　} \ $と大きさも方向も全く相等しいことに注意すれば，結局，求める外部磁束は$ \ \fbox {　（４）　} \ $の$ \ 2 \ $倍となる。

したがって，無限に長い$ \ 2 \ $本の平行往復回路の長さ$ \ l \ $についての導線外部の磁束による導線外部自己インダクタンスは$ \ \fbox {　（５）　} \ $となる。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {\mu _{0}I}{2\pi r}l\mathrm {d}r　　　　　&（ロ）&　\frac {\mu _{0}lI}{2\pi}\log _{\mathrm {e}} \frac {d}{a}　　　　　&（ハ）&　\frac {\mu _{0}l}{3\pi d^{3}} \\[ 5pt ] &（ニ）&　\frac {\mu _{0}l}{\pi}\log _{\mathrm {e}} \frac {d}{a}　　　　　　　&（ホ）&　\frac {I}{2\pi r}　　　　　&（ヘ）&　\frac {I}{\pi r^{2}} \\[ 5pt ] &（ト）&　\frac {2\mu _{0}l}{3\pi d^{3}}　　　　　&（チ）&　\frac {\mu _{0}lI}{3\pi d^{3}}　　　　　　　&（リ）&　\frac {I}{2\pi r^{2}} \\[ 5pt ] &（ヌ）&　\frac {\mu _{0}I}{2\pi r^{2}}l\mathrm {d}r　　　　　&（ル）&　a \ から \ d-2a　　　　　　&（ヲ）&　a \ から \ d-a \\[ 5pt ] &（ワ）&　0 \ から \ d-a　　　　　&（カ）&　\frac {\mu _{0}I}{\pi r^{2}}l\mathrm {d}r　　　　　　&（ヨ）&　\frac {\mu _{0}lI}{6\pi d^{3}} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

平行往復線路の自己インダクタンスに関する問題です。
途中の積分計算等数学的な要素が強い問題ですが，$ \ 2 \ $種理論でも扱ってきたような内容なので，$ \ 1 \ $種受験生ですと多くの方が完答されるかと思います。
ぜひ中身を理解して完答を目指すようにして下さい。

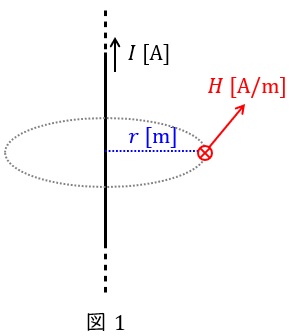
1.アンペア（アンペール）の周回積分の法則
空間上の磁界ベクトルを$ \ \boldsymbol H \ $，$ \ \mathrm {C} \ $を閉曲線，$ \ \mathrm {d}\boldsymbol l \ $を$ \ \mathrm {C} \ $上の微小区間ベクトル，$ \ I \ $を$ \ \mathrm {C} \ $と鎖交する電流の総量とすると，
\[
\begin{eqnarray}
\oint_{\mathrm {C}} \boldsymbol H \cdot \mathrm {d}\boldsymbol l &=&I　 \\[ 5pt ] \end{eqnarray}
\] の関係があり，これをアンペアの周回積分の法則といいます。
例えば，図1のように無限長直線電流$ \ I \ \mathrm {[A]} \ $が流れているとき，電線から距離$ \ r \ \mathrm {[m]} \ $の位置での磁界の強さ$ \ H \ \mathrm {[A / m]} \ $は，$ \ l=2\pi r \ $なので，
\[
\begin{eqnarray}
2\pi r H&=&I \\[ 5pt ] H&=&\frac {I}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] となります。

2.磁束密度$ \ B \ $
単位面積あたりに通過する磁束のことで，微小な面積$ \ \mathrm {d}\boldsymbol S \ $を通過する磁束が$ \ \mathrm {d}\mathit {\Phi } \ $であるとき，磁束密度$ \ \boldsymbol B \ $との関係は，
\[
\begin{eqnarray}
\mathrm {d}\mathit {\Phi }&=&\boldsymbol B\cdot \mathrm {d}\boldsymbol S \\[ 5pt ] \mathit {\Phi }&=&\int_{\mathrm {S}} \boldsymbol B\cdot \mathrm {d}\boldsymbol S \\[ 5pt ] \end{eqnarray}
\] となります。

3.磁束密度$ \ B \ $と磁界の大きさ$ \ H \ $の関係
透磁率が$ \ \mu \ \mathrm {[H / m]} \ $の時，磁束密度$ \ B \ \mathrm {[T]} \ $と磁界の大きさ$ \ H \ \mathrm {[A / m]} \ $の関係は，
\[
\begin{eqnarray}
B&=&\mu H \\[ 5pt ] \end{eqnarray}
\] となります。

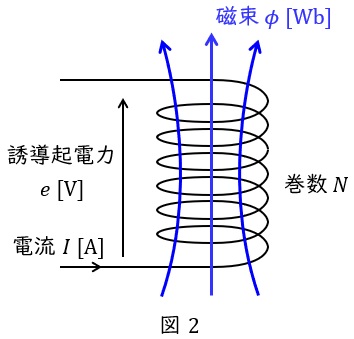
4.ファラデーの電磁誘導の法則と自己インダクタンス$ \ L \ $
図2において，巻数$ \ N \ $のコイルを貫通する磁束$ \ \phi \ \mathrm {[Wb]} \ $があるとき，ファラデーの電磁誘導の法則より，コイルに発生する誘導起電力$ \ e \ \mathrm {[V]} \ $は，磁束の時間変化に比例し，
\[
\begin{eqnarray}
e&=&−N\frac {\mathrm {d}\phi }{\mathrm {d}t} \\[ 5pt ] \end{eqnarray}
\] で求められます。これをファラデーの電磁誘導の法則といいます。このとき，電流変化によりコイル内の磁束が変化したと考えれば，
\[
\begin{eqnarray}
e&=&−L\frac {\mathrm {d}I }{\mathrm {d}t} \\[ 5pt ] \end{eqnarray}
\] という関係も成り立ち，$ \ L \ \mathrm {[H]} \ $を自己インダクタンスと言います。これらの関係から，
\[
\begin{eqnarray}
−N\frac {\mathrm {d}\phi }{\mathrm {d}t}&=&−L\frac {\mathrm {d}I }{\mathrm {d}t} \\[ 5pt ] N\phi &=&LI \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

(1)解答：ホ
導線$ \ 1 \ $の電流$ \ I \ $による中心軸からの距離$ \ r \ $での磁界$ \ H \ $は，ワンポイント解説「1.アンペア（アンペール）の周回積分の法則」の通り，
\[
\begin{eqnarray}
H&=&\frac {I}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：イ
(1)より，導線$ \ 1 \ $の中心軸からの距離$ \ r \ $における磁束密度$ \ B \ $は，ワンポイント解説「3.磁束密度$ \ B \ $と磁界の大きさ$ \ H \ $の関係」の通り，
\[
\begin{eqnarray}
B&=&\mu _{0}H \\[ 5pt ] &=&\frac {\mu _{0}I}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] となるので，幅$ \ \mathrm {d}r \ $，長さ$ \ l \ $の帯状面積$ \ \mathrm {d}S=l\mathrm {d}r \ $を貫く磁束$ \ \mathrm {d}\phi \ $は，ワンポイント解説「2.磁束密度$ \ B \ $」の通り，
\[
\begin{eqnarray}
\mathrm {d}\phi &=&B\mathrm {d}S \\[ 5pt ] &=&\frac {\mu _{0}I}{2\pi r}l\mathrm {d}r \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ヲ
外部磁束$ \ \mathit {\Phi } \ $は$ \ 2 \ $本の導線間を通過している磁束なので，積分範囲は$ \ a \ $から$ \ d-a \ $となる。

(4)解答：ロ
$ \ a ≪d \ $に注意して，(2)解答式を両辺積分すると，
\[
\begin{eqnarray}
\mathit {\Phi } &=&\int _{a}^{d-a} \frac {\mu _{0}I}{2\pi r}l\mathrm {d}r \\[ 5pt ] &=&\frac {\mu _{0}lI}{2\pi }\int _{a}^{d-a} \frac {1}{r}\mathrm {d}r \\[ 5pt ] &=&\frac {\mu _{0}lI}{2\pi }\left[ \log _\mathrm {e}r\right] _{a}^{d-a} \\[ 5pt ] &=&\frac {\mu _{0}lI}{2\pi }\left\{ \log _\mathrm {e} \left( d-a\right) -\log _\mathrm {e}a \right\} \\[ 5pt ] &=&\frac {\mu _{0}lI}{2\pi } \log _\mathrm {e} \frac {d-a}{a} \\[ 5pt ] &≃&\frac {\mu _{0}lI}{2\pi } \log _\mathrm {e} \frac {d}{a} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ニ
題意より，求める外部磁束$ \ \mathit {\Phi }^{\prime } \ $は$ \ \mathit {\Phi } \ $の$ \ 2 \ $倍なので，
\[
\begin{eqnarray}
\mathit {\Phi }^{\prime } &=&2\mathit {\Phi } \\[ 5pt ] &=&\frac {\mu _{0}lI}{\pi } \log _\mathrm {e} \frac {d}{a} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，自己インダクタンス$ \ L \ $は，ワンポイント解説「4.ファラデーの電磁誘導の法則と自己インダクタンス$ \ L \ $」の通り，
\[
\begin{eqnarray}
\mathit {\Phi }^{\prime } &=&LI \\[ 5pt ] L&=&\frac {\mathit {\Phi }^{\prime }}{I} \\[ 5pt ] &=&\frac {\displaystyle \frac {\mu _{0}lI}{\pi } \log _\mathrm {e} \frac {d}{a}}{I} \\[ 5pt ] &=&\frac {\mu _{0}l}{\pi}\log _{\mathrm {e}} \frac {d}{a} \\[ 5pt ] \end{eqnarray}
\] と求められる。