Contents
【問題】
【難易度】★★★☆☆(普通)
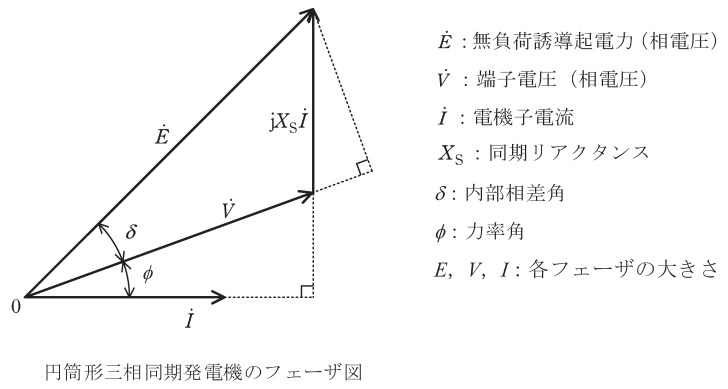
図は,三相星形接続の円筒形同期発電機のフェーザ図である。この図を参照して次の問に答えよ。ただし,電機子抵抗による電圧降下及び磁気飽和は無視するものとする。
(1) \(E \ \mathrm {[V]}\),\(V \ \mathrm {[V]}\),\(\delta \ \mathrm {[rad]}\),\(X_{\mathrm {S}} \ \mathrm {[\Omega ]} \ \)を用いて,発電機出力\( \ P \ \mathrm {[kW]} \ \)を表す式を導出過程を含めて示せ。
(2) 定格皮相電力\( \ 30000 \ \mathrm {kV\cdot A}\),定格端子電圧(線間電圧)\( \ 6600 \ \mathrm {V}\),短絡比\( \ 0.5 \ \)の円筒形三相同期発電機において,次のa,b及びcの問に答えよ。
a.\(X_{\mathrm {S}} \ \mathrm {[\Omega ]} \ \)の値を求めよ。
b.三相平衡交流系統に接続して,\(E=7000 \ \mathrm {V}\),\(V=3810 \ \mathrm {V}\),\(\displaystyle \delta =\frac {\pi }{6}\ \mathrm {rad} \ \)で運転しているときの\( \ P \ \mathrm {[kW]}\),\(I \ \mathrm {[A]}\),力率(\(\cos \phi \))の値を求めよ。
c.この発電機を三相平衡交流系統から切り離して,三相平衡抵抗器負荷に接続した。界磁電流を調整して\( \ V=3700 \ \mathrm {V}\),\(\displaystyle \delta =\frac {\pi }{3}\ \mathrm {rad} \ \)で運転し,抵抗器負荷に電力を供給した。このときの\( \ P \ \mathrm {[kW]}\),\(E \ \mathrm {[V]}\),\(I \ \mathrm {[A]}\),力率(\(\cos \phi \))の値を求めよ。
【ワンポイント解説】
(1)の問題が二次試験らしい問題と言えると思います。導出過程もそれほど難しいわけではないので,導出過程も理解するようにしましょう。この問題はぱっと見易しそうな問題ですが,単位を揃えたり,途中の計算が複雑であったり落とし穴の多い問題です。計算は慎重かつ速やかにできるようにしましょう。
1.同期発電機の一相分の出力\(P\)
無負荷誘導起電力\( \ E \ \mathrm {[V]}\),端子電圧(相電圧)\( \ V \ \mathrm {[V]}\),内部相差角\( \ \delta \ \mathrm {[rad]}\),同期リアクタンス\( \ X_{\mathrm {S}} \ \mathrm {[\Omega ]} \ \)とすると,一相分の出力\(P\)は,
\[
\begin{eqnarray}
P &=&\frac {EV}{X_{\mathrm {S}}}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.同期機における短絡比と同期リアクタンスの関係
短絡比\( \ K_{\mathrm {s}} \ \)は三相短絡電流を\( \ I_{\mathrm {s}} \ \),定格電流\( \ I_{\mathrm {n}} \ \)とすると,
\[
\begin{eqnarray}
K_{\mathrm {s}} &=&\frac {I_{\mathrm {s}}}{I_{\mathrm {n}}} \\[ 5pt ]
\end{eqnarray}
\]
で定義されます。一方,同期リアクタンス\( \ X_{\mathrm {s}} \ \)は抵抗分を無視すると,定格相電圧\( \ E_{\mathrm {n}} \ \)と三相短絡電流\( \ I_{\mathrm {s}} \ \)を用いて,
\[
\begin{eqnarray}
X_{\mathrm {s}} &=&\frac {E_{\mathrm {n}}}{I_{\mathrm {s}}} \ [\Omega] \\[ 5pt ]
\end{eqnarray}
\]
となりこれを単位法で表すと,
\[
\begin{eqnarray}
X_{\mathrm {s}} \ \mathrm {[p.u.]} &=&\frac {X_{\mathrm {s}} \ [\Omega ] }{X_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {E_{\mathrm {n}}}{I_{\mathrm {s}}}}{\displaystyle \frac {E_{\mathrm {n}}}{I_{\mathrm {n}}}} \\[ 5pt ]
&=&\frac {I_{\mathrm {n}}}{I_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
となります。よって単位法で表した同期リアクタンスは短絡比の逆数となります。
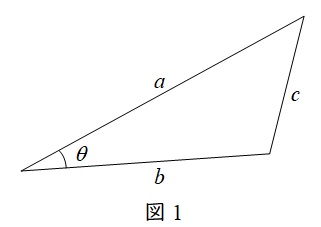
3.余弦定理
図1のような任意の三角形について,以下の等式が成り立ちます。
\[
\begin{eqnarray}
c^{2} &=&a^{2}+b^{2}-2ab\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)\(E \ \mathrm {[V]}\),\(V \ \mathrm {[V]}\),\(\delta \ \mathrm {[rad]}\),\(X_{\mathrm {S}} \ \mathrm {[\Omega ]} \ \)を用いて,発電機出力\( \ P \ \mathrm {[kW]} \ \)を表す式
フェーザ図より,
\[
\begin{eqnarray}
E\sin \delta &=&{X_{\mathrm {s}}}I \cos \phi &・・・・・・・・①& \\[ 5pt ]
P&=&3VI\cos \phi \times 10^{-3} &・・・・・・・・②& \\[ 5pt ]
\end{eqnarray}
\]
の関係があることが分かる。①より,
\[
\begin{eqnarray}
I\cos \phi &=&\frac {E\sin \delta }{X_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,これを②に代入すると,
\[
\begin{eqnarray}
P&=&3V\cdot \frac {E\sin \delta }{X_{\mathrm {s}}} \times 10^{-3} \\[ 5pt ]
&=&\frac {3EV}{X_{\mathrm {s}}}\sin \delta \times 10^{-3} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)a.\(X_{\mathrm {S}} \ \mathrm {[\Omega ]} \ \)の値
ワンポイント解説「2.同期機における短絡比と同期リアクタンスの関係」より,
\[
\begin{eqnarray}
X_{\mathrm {S}}&=&\frac {1}{K_{\mathrm {s}}} \\[ 5pt ]
&=&\frac {1}{0.5} \\[ 5pt ]
&=&2 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,これをオーム値に換算すると,
\[
\begin{eqnarray}
X_{\mathrm {S}} \mathrm {[p.u.]} &=&\frac {P_{\mathrm {n}}}{V_{\mathrm {n}}^{2}} X_{\mathrm {S}} \mathrm {[\Omega ]} \\[ 5pt ]
X_{\mathrm {S}} \mathrm {[\Omega ]}&=&\frac {V_{\mathrm {n}}^{2}}{P_{\mathrm {n}}}X_{\mathrm {S}} \mathrm {[p.u.]} \\[ 5pt ]
&=&\frac {{6600}^{2}}{30000000}\times 2 \\[ 5pt ]
&=&2.904 → 2.90 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)b.\(E=7000 \ \mathrm {V}\),\(V=3810 \ \mathrm {V}\),\(\displaystyle \delta =\frac {\pi }{6}\ \mathrm {rad} \ \)で運転しているときの\( \ P \ \mathrm {[kW]}\),\(I \ \mathrm {[A]}\),力率(\(\cos \phi \))の値
(1)の解答式に各値を代入すると,
\[
\begin{eqnarray}
P&=&\frac {3EV}{X_{\mathrm {s}}}\sin \delta \times 10^{-3} \\[ 5pt ]
&=&\frac {3\times 7000\times 3810}{2.904}\times \sin \frac {\pi }{6} \times 10^{-3} \\[ 5pt ]
&=&\frac {3\times 7000\times 3810}{2.904}\times \frac {1}{2} \times 10^{-3} \\[ 5pt ]
&≒&13776 → 13800 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
となる。フェーザ図において,ワンポイント解説「3.余弦定理」より,
\[
\begin{eqnarray}
\left( X_{\mathrm {S}}I\right) ^{2} &=&E^{2}+V^{2}-2EV\cos \delta \\[ 5pt ]
I &=&\frac {\sqrt {E^{2}+V^{2}-2EV\cos \delta }}{X_{\mathrm {S}}} \\[ 5pt ]
&=&\frac {\displaystyle \sqrt {7000^{2}+3810^{2}-2\times 7000 \times 3810 \times \cos \frac {\pi}{6} }}{2.904} \\[ 5pt ]
&=&\frac {\displaystyle \sqrt {7000^{2}+3810^{2}-2\times 7000 \times 3810 \times \frac {\sqrt {3}}{2} }}{2.904} \\[ 5pt ]
&≒&1433.2 → 1430 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。これらを②に代入すると,
\[
\begin{eqnarray}
P&=&3VI\cos \phi \times 10^{-3} \\[ 5pt ]
\cos \phi &=&\frac {P}{3VI}\times 10^{3} \\[ 5pt ]
&=&\frac {13776}{3\times 3810\times 1433.2}\times 10^{3} \\[ 5pt ]
&≒&0.84095 → 0.841 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)c.\( \ V=3700 \ \mathrm {V}\),\(\displaystyle \delta =\frac {\pi }{3}\ \mathrm {rad} \ \)で運転し,抵抗器負荷に電力を供給したときの\( \ P \ \mathrm {[kW]}\),\(E \ \mathrm {[V]}\),\(I \ \mathrm {[A]}\),力率(\(\cos \phi \))の値
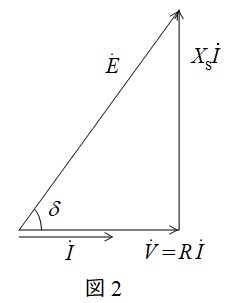
題意に沿ってフェーザ図を描くと図2のようになる。フェーザ図より,
\[
\begin{eqnarray}
E\cos \delta &=&V \\[ 5pt ]
E&=&\frac {V}{\cos \delta } \\[ 5pt ]
&=&\frac {3700}{\displaystyle \cos \frac {\pi }{3}} \\[ 5pt ]
&=&\frac {3700}{0.5} \\[ 5pt ]
&=&7400 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。(1)の解答式に各値を代入すると,
\[
\begin{eqnarray}
P&=&\frac {3EV}{X_{\mathrm {s}}}\sin \delta \times 10^{-3} \\[ 5pt ]
&=&\frac {3\times 7400\times 3700}{2.904}\times \sin \frac {\pi }{3} \times 10^{-3} \\[ 5pt ]
&=&\frac {3\times 7400\times 3700}{2.904}\times \frac {\sqrt {3}}{2} \times 10^{-3} \\[ 5pt ]
&≒&24496 → 24500 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。これらの値を②に代入すると,
\[
\begin{eqnarray}
P&=&3VI\cos \phi \times 10^{-3} \\[ 5pt ]
I&=&\frac {P}{3V\cos \phi }\times 10^{3} \\[ 5pt ]
&=&\frac {24496}{\displaystyle 3\times 3700\times 1}\times 10^{3} \\[ 5pt ]
&≒&2206.8 → 2210 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
また,抵抗負荷なので\( \ \cos \phi =1 \ \)である。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは