【問題】
【難易度】★★★★☆(やや難しい)
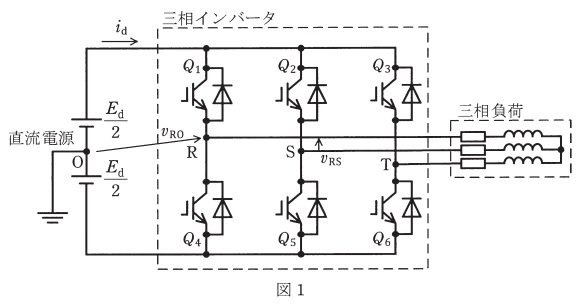
図1には,\( \ \mathrm {R} \ \)相→\( \ \mathrm {S} \ \)相→\( \ \mathrm {T} \ \)相の相順で,\( \ \mathrm {180°} \ \)通電モードで運転する三相インバータとその三相負荷の回路を示す。直流電圧を\( \ E_{\mathrm {d}} \ \)一定,三相インバータ内には損失がないものとして,次の問に答えよ。
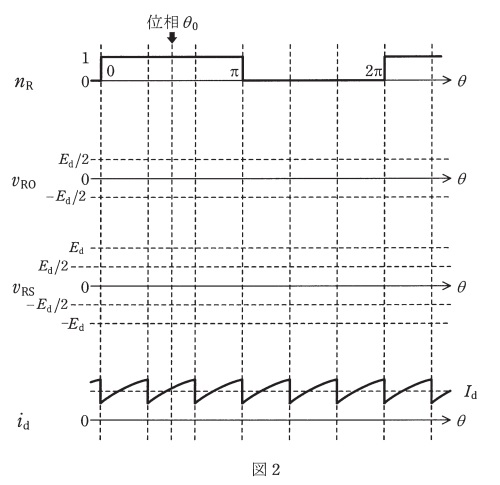
(1) 図2は三相インバータの動作を説明する図であり,波形\( \ n_{\mathrm {R}} \ \)は\( \ \mathrm {R} \ \)相のノッチ波である。ノッチ波は\( \ 1 \ \)のときにプラス側のパワーデバイスをオンし,\( \ 0 \ \)のときにマイナス側のパワーデバイスをオンすることを意味している。図2の位相\( \ \theta _{\mathrm {0}} \ \)において,オン信号を与えているパワーデバイスは,\( \ \mathrm {R} \ \)相では\( \ Q_{1} \ \)であるが,\( \ \mathrm {S} \ \)相及び\( \ \mathrm {T} \ \)相ではどのパワーデバイスであるかを答えよ。
(2) 答案用紙に図2と同じ図が印刷されているので,図1の\( \ \mathrm {R} \ \)相電圧\( \ v _{\mathrm {RO}} \ \),\( \ \mathrm {R}\)-\(\mathrm {S} \ \)相線間電圧圧\( \ v _{\mathrm {RS}} \ \)の波形を,波形の大きさとスイッチングの位相が明確に分かるように,太線で明確に描け。ただし,\( \ v _{\mathrm {RO}} \ \)の基準電位点\( \ \mathrm {O} \ \)とする。
(3) 上記小問(2)において,二つの電圧波形\( \ v _{\mathrm {RO}} \ \),\( \ v _{\mathrm {RS}} \ \)のうち,出力周波数に対して\(3\)の整数倍次数の高調波が含まれている波形はどちらの波形であるかを答えよ。
(4) 上記小問(2)において,線間電圧\( \ v _{\mathrm {RS}} \ \)の実効値\( \ E_{0} \ \)を表す式を,\( \ E _{\mathrm {d}} \ \)を用いて示せ。
(5) 負荷電流が正弦波であるとみなせるとき,ある遅れの力率の場合の直流電流\( \ i _{\mathrm {d}} \ \)の波形を図2の最下段に示している。負荷に供給される有効電力が\( \ P=50 \ \mathrm {kW} \ \),力率が\( \ \displaystyle \cos \phi =\frac {\sqrt {3}}{2} \ \)であり,\( \ E _{\mathrm {d}}=200 \ \mathrm {V} \ \)であった場合の直流電流の平均値\( \ I _{\mathrm {d}} \ [ \mathrm {A} ] \ \)を求めよ。
【ワンポイント解説】
(3)の高調波に関する問題はフーリエ級数展開を要するため,難易度が高いですが,その他の問題は比較的易しい問題となっています。(4)の実効値の定義は他の科目でも出題されることがあるので,必ず理解するようにしましょう。
1.フーリエ級数展開
\( \ f( \theta ) \ \)を周期\( \ 2 \pi \ \)の周期関数であるとしたとき,
\[
\begin{eqnarray}
f\left( \theta \right) &=& a_{0}+\displaystyle \sum_{ n = 1 }^{ \infty } \left( a_{n} \cos n\theta + b_{n} \sin n\theta \right) \\[ 5pt ]
a_{0}&=& \frac {1}{2\pi }\int _{0}^{2\pi} f\left( \theta \right) \mathrm {d}\theta \\[ 5pt ]
a_{n}&=& \frac {1}{\pi }\int _{0}^{2\pi} f\left( \theta \right) \cos n\theta \mathrm {d}\theta \\[ 5pt ]
b_{n}&=& \frac {1}{\pi }\int _{0}^{2\pi} f\left( \theta \right) \sin n\theta \mathrm {d}\theta
\end{eqnarray}
\]
とすると,\( \ f( \theta ) \ \)のフーリエ級数展開ができます。
(具体的には設問中の解答で示します。)
フーリエ級数展開について、メカニズム等もう少し詳しく知りたい方は、こちらの本で学習してみて下さい。非常に分かりやすく理解が深まると思います。
2.平均値と実効値の定義
\( \ f( \theta ) \ \)を周期\( \ 2 \pi \ \)の周期関数であるとしたとき,平均値と実効値は以下の通りとなります。
①平均値\( \ F_{\mathrm {av}} \ \)
\[
\begin{eqnarray}
F_{\mathrm {av}}&=&\frac {1}{2\pi }\int _{0}^{2\pi }f( \theta ) \mathrm {d}\theta \\[ 5pt ]
\end{eqnarray}
\]
②実効値\( \ F \ \)
\[
\begin{eqnarray}
F&=&\sqrt {\frac {1}{2\pi} \int _{0}^{2\pi} f( \theta ) ^{2} \mathrm {d}\theta } \\[ 5pt ]
\end{eqnarray}
\]
【関連する「電気の神髄」記事】
三相電圧形インバータ(2レベルインバータ)
さまざまな交流波形のフーリエ級数展開まとめ
【解答】
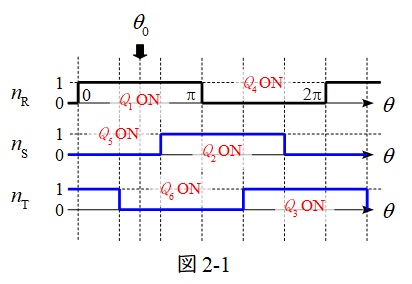
(1)位相\( \ \theta _{\mathrm {0}} \ \)において,\( \ \mathrm {S} \ \)相及び\( \ \mathrm {T} \ \)相でオン信号を与えているパワーデバイス
\( \ \mathrm {S} \ \)相及び\( \ \mathrm {T} \ \)相では\( \ \mathrm {R} \ \)相から順に\( \ \displaystyle \frac {2}{3}\pi \ \)ずつ位相がずれているため,パワーデバイスのオンオフのタイミングは図2-1の通りとなる。
よって,位相\( \ \theta _{0} \ \)の時オンとなっているデバイスは\( \ \mathrm {S} \ \)相が\( \ Q_{\mathrm {5}} \ \),\( \ \mathrm {T} \ \)相が\( \ Q_{\mathrm {6}} \ \)となる。
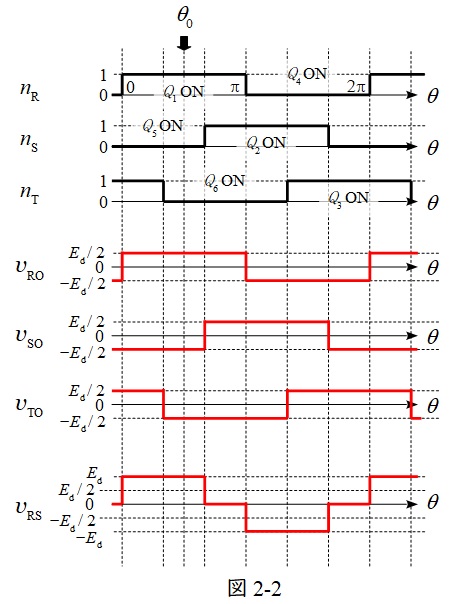
(2)\( \ v _{\mathrm {RO}} \ \),\( \ v _{\mathrm {RS}} \ \)の波形
\( \ \mathrm {R} \ \)の電位は\( \ Q_{\mathrm {1}} \ \)がオンの時\( \ \displaystyle \frac {E_{\mathrm {d}}}{2} \ \), \( \ Q_{\mathrm {4}} \ \)がオンの時\( \ \displaystyle -\frac {E_{\mathrm {d}}}{2} \ \)となる。また,\( \ v _{\mathrm {RS}} \ \)は\( \ v _{\mathrm {RS}}=v _{\mathrm {RO}}-v _{\mathrm {SO}} \ \)である。よって,波形は図2-2のようになる。(参考で\( \ v _{\mathrm {SO}} \ \)と\( \ v _{\mathrm {TO}} \ \)の波形も描いています。)
(3)出力周波数に対して\(3\)の整数倍次数の高調波が含まれている波形
図2-2より,\( \ v _{\mathrm {RO}} \ \)の波形は,
\[
\begin{eqnarray}
v _{\mathrm {RO}}=
\begin{cases}
\displaystyle \frac {E_{\mathrm {d}}}{2} & ( 0 < \theta ≦ \pi ) \\[ 5pt ]
\displaystyle -\frac {E_{\mathrm {d}}}{2} & ( \pi < \theta ≦ 2\pi )
\end{cases}
\end{eqnarray}
\]
である。ワンポイント解説「1.フーリエ級数展開」より,フーリエ級数は,
\[
\begin{eqnarray}
v _{\mathrm {RO}} &=& a_{0}+\displaystyle \sum_{ n = 1 }^{ \infty } \left( a_{n} \cos n\theta + b_{n} \sin n\theta \right) &・・・・・①&\\[ 5pt ]
a_{0}&=& \frac {1}{2\pi }\int _{0}^{2\pi} v _{\mathrm {RO}} \mathrm {d}\theta &・・・・・②& \\[ 5pt ]
a_{n}&=& \frac {1}{\pi }\int _{0}^{2\pi} v _{\mathrm {RO}} \cos n\theta \mathrm {d}\theta &・・・・・③& \\[ 5pt ]
b_{n}&=& \frac {1}{\pi }\int _{0}^{2\pi} v _{\mathrm {RO}} \sin n\theta \mathrm {d}\theta &・・・・・④&
\end{eqnarray}
\]
で与えられる。②より,
\[
\begin{eqnarray}
a_{0}&=& \frac {1}{2\pi }\left\{ \int _{0}^{\pi} \frac {E_{\mathrm {d}}}{2} d\theta + \int _{\pi}^{2\pi} \left( -\frac {E_{\mathrm {d}}}{2} \right) \mathrm {d}\theta \right\} \\[ 5pt ]
&=& \frac {1}{2\pi }\left( \left[ \frac {E_{\mathrm {d}}}{2}\theta \right] _{0}^{\pi} + \left[ -\frac {E_{\mathrm {d}}}{2}\theta \right] _{\pi}^{2\pi} \right) \\[ 5pt ]
&=& 0 ・・・・・②^{\prime }
\end{eqnarray}
\]
となる。③より,
\[
\begin{eqnarray}
a_{n}&=& \frac {1}{\pi }\int _{0}^{2\pi} v _{\mathrm {RO}} \cos n\theta \mathrm {d}\theta \\[ 5pt ]
&=& \frac {1}{\pi }\left( \int _{0}^{\pi} \frac {E_{\mathrm {d}}}{2} \cos n\theta \mathrm {d}\theta +\int _{\pi}^{2\pi} -\frac {E_{\mathrm {d}}}{2} \cos n\theta \mathrm {d}\theta \right) \\[ 5pt ]
&=& \frac {1}{\pi }\left( \left[ \frac {E_{\mathrm {d}}}{2n} \sin n\theta \right] _{0}^{\pi} +\left[ -\frac {E_{\mathrm {d}}}{2n} \sin n\theta \right] _{\pi}^{2\pi} \right) \\[ 5pt ]
&=& 0 ・・・・・③^{\prime }
\end{eqnarray}
\]
となる。④より,
\[
\begin{eqnarray}
b_{n}&=& \frac {1}{\pi }\int _{0}^{2\pi} v _{\mathrm {RO}} \sin n\theta \mathrm {d}\theta \\[ 5pt ]
&=& \frac {1}{\pi }\left( \int _{0}^{\pi} \frac {E_{\mathrm {d}}}{2} \sin n\theta \mathrm {d}\theta +\int _{\pi}^{2\pi} -\frac {E_{\mathrm {d}}}{2} \sin n\theta \mathrm {d}\theta \right) \\[ 5pt ]
&=& \frac {1}{\pi }\left( \left[ -\frac {E_{\mathrm {d}}}{2n} \cos n\theta \right] _{0}^{\pi} +\left[ \frac {E_{\mathrm {d}}}{2n} \cos n\theta \right] _{\pi}^{2\pi} \right) \\[ 5pt ]
&=& \frac {E_{\mathrm {d}}}{2n\pi }\left( 1- 2\cos n\pi +\cos 2n\pi \right)
\end{eqnarray}
\]
すなわち,
\[
\begin{eqnarray}
b_{n}=
\begin{cases}
\displaystyle \frac {2E_{\mathrm {d}}}{n\pi } & ( nが奇数の時 ) ・・・・・④^{\prime }\\[ 5pt ]
\displaystyle 0 & ( nが偶数の時 ) ・・・・・⑤^{\prime }
\end{cases}
\end{eqnarray}
\]
となる。\(②^{\prime }~⑤^{\prime }\)を①に代入すると,
\[
\begin{eqnarray}
v _{\mathrm {RO}} &=& a_{0}+\displaystyle \sum_{ n = 1 }^{ \infty } \left( a_{n} \cos n\theta + b_{n} \sin n\theta \right) \\[ 5pt ]
&=& \frac {2E_{\mathrm {d}}}{\pi }\left( \sin \theta + \frac {1}{3}\sin 3\theta + \frac {1}{5}\sin 5\theta +・・・\right)
\end{eqnarray}
\]
となるので,\( \ v _{\mathrm {RO}} \ \)は\( \ 3 \ \)の整数倍次数の高調波が含まれていることがわかる。同様に\( \ v _{\mathrm {RS}} \ \)についても求めると,
\[
\begin{eqnarray}
a_{0}&=& 0 \\[ 5pt ]
a_{n}&=& \frac {E_{\mathrm {d}}}{n\pi }\left( \sin \frac {2n\pi }{3}-\sin \frac {5n\pi }{3}\right) \\[ 5pt ]
b_{n}&=& \frac {E_{\mathrm {d}}}{n\pi } \left( 1-\cos \frac {2n\pi }{3}-\cos n\pi +\cos \frac {5n\pi }{3}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
v _{\mathrm {RS}} &=&\frac {\sqrt {3}E}{\pi }\left( \cos \theta -\frac {1}{5}\cos 5\theta +\frac {1}{7}\cos 7\theta +\cdots \right) +\frac {3E_{\mathrm {d}}}{\pi }\left( \sin \theta +\frac {1}{5}\sin 5\theta +\frac {1}{7}\sin 7\theta +\cdots \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められ,\( \ v _{\mathrm {RS}} \ \)は\( \ 3 \ \)の整数倍次数の高調波が含まれないことがわかる。
\[\]
(4)\( \ v _{\mathrm {RS}} \ \)の実効値
ワンポイント解説「2.平均値と実効値の定義」より,線間電圧\( \ v _{\mathrm {RS}} \ \)の実効値\( \ E_{0} \ \)は,
\[
\begin{eqnarray}
E_{0}&=& \sqrt {\frac {1}{2\pi} \int _{0}^{2\pi} v _{\mathrm {RS}} ^{2} \mathrm {d}\theta } \\[ 5pt ]
&=& \frac {1}{\sqrt {2\pi}} \sqrt {\int _{0}^{\frac {2}{3}\pi} E_{\mathrm {d}} ^{2} \mathrm {d}\theta +\int _{\pi}^{\frac {5}{3}\pi} \left( -E_{\mathrm {d}}\right) ^{2} \mathrm {d}\theta }\\[ 5pt ]
&=& \frac {1}{\sqrt {2\pi}} \sqrt {\left[ E_{\mathrm {d}} ^{2} \theta \right] _{0}^{\frac {2}{3}\pi} +\left[ E_{\mathrm {d}} ^{2} \theta \right] _{\pi}^{\frac {5}{3}\pi}} \\[ 5pt ]
&=& \sqrt{\frac {2}{3}}E_{\mathrm {d}}
\end{eqnarray}
\]
と求められる。
(5)直流電流の平均値\( \ I_{\mathrm {d}} \ \)
題意より三相インバータには損失がないので,出力の有効電力と,直流入力の電力は等しい。よって,直流電力\( \ P=50 \ \mathrm {kW} \ \)は直流電圧\( \ E_{\mathrm {d}}=200 \ \mathrm {V} \ \)と\( \ I_{\mathrm {d}} \ \)の積となるから,
\[
\begin{eqnarray}
I_{\mathrm {d}}&=& \frac {P}{E_{\mathrm {d}}} \\[ 5pt ]
&=& \frac {50000}{200} \\[ 5pt ]
&=& 250 \ [ \mathrm {A} ]
\end{eqnarray}
\]
と求められる。













 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは