Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
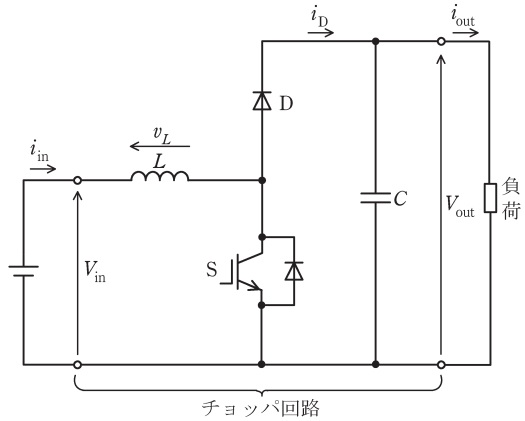
図は\( \ \mathrm {IGBT} \ \)をスイッチングデバイス\( \ \mathrm {S} \ \)(以下,デバイス\( \ \mathrm {S} \ \)と略す)に用いたチョッパ回路である。このチョッパの機能は,キャパシタンス\( \ C \ \)のコンデンサとリアクタンス\( \ L \ \)のリアクトルの働きによって実現されている。入力は直流電圧\( \ V_{\mathrm {in}} \ \)(一定値),出力は\( \ V_{\mathrm {out}} \ \)である。デバイス\( \ \mathrm {S} \ \)は,\( \ T_{\mathrm {on}} \ \)の時間はオン,\( \ T_{\mathrm {off}} \ \)の時間はオフを繰り返し,周期は一定で,\( \ T_{\mathrm {on}}+T_{\mathrm {off}} \ \)である。入力電流\( \ i_{\mathrm {in}}>0 \ \),全ての回路素子は理想的と仮定して,次の問に答えよ。
(1) このチョッパ回路は太陽光発電でよく用いられている。その理由についてチョッパ回路の\( \ V_{\mathrm {in}} \ \)と\( \ V_{\mathrm {out}} \ \)の大小関係に触れつつ簡単に述べよ。
(2) \( \ T_{\mathrm {on}} \ \)の時間において,リアクトルの電圧\( \ v_{\mathrm {L}} \ \)を求めよ。また,求めた式をもとに電流\( \ i_{\mathrm {in}} \ \)は増加するか,減少するか述べよ。
(3) \( \ T_{\mathrm {off}} \ \)の時間において,リアクトルの電圧\( \ v_{\mathrm {L}} \ \)を求めよ。また,求めた式をもとに電流\( \ i_{\mathrm {in}} \ \)は増加するか,減少するか述べよ。
次に,コンデンサのキャパシタンス\( \ C \ \)は十分に大きく,チョッパの出力電圧は一定値\( \ V_{\mathrm {out}} \ \)に平滑されているものとする。さらに,電流\( \ i_{\mathrm {in}} \ \)のリプルが十分に小さく一定値\( \ I_{\mathrm {in}} \ \)と見なせると仮定する。このとき
(4) ダイオード\( \ \mathrm {D} \ \)に流れる電流\( \ i_{\mathrm {D}} \ \)の平均値\( \ I_{\mathrm {D}} \ \)を\( \ T_{\mathrm {on}} \ \),\( \ T_{\mathrm {off}} \ \),\( \ I_{\mathrm {in}} \ \)を用いて示せ。
(5) 出力電圧\( \ V_{\mathrm {out}} \ \)を\( \ T_{\mathrm {on}} \ \),\( \ T_{\mathrm {off}} \ \),\( \ V_{\mathrm {in}} \ \)を用いて示せ。
【ワンポイント解説】
昇圧チョッパに関する問題です。
計算量が少ない問題であるため,昇圧チョッパのメカニズムを理解している受験生ならば短時間で完答が目指せる問題です。
降圧チョッパや昇降圧チョッパに関する問題も出題されることがあるので,合わせて理解しておくようにしましょう。
1.昇圧チョッパ
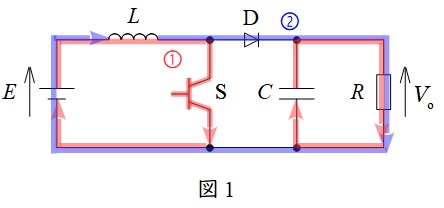
図1に昇圧チョッパの例を示します。
スイッチ\( \ \mathrm {S} \ \)が\( \ \mathrm {ON} \ \)時は①のように導通し,電源\( \ E \ \)からリアクトル\( \ L \ \)にエネルギー\( \ EIT_{\mathrm {on}} \ \)が蓄えられ,出力側はコンデンサ\( \ C \ \)から電荷が供給されます。
スイッチ\( \ \mathrm {OFF} \ \)時は②のように導通し,リアクトル\( \ L \ \)に蓄えられたエネルギー\( \ \displaystyle L\frac {\mathrm {d}i}{\mathrm {d}t}IT_{\mathrm {off}} \ \)が放出されます。定常状態では蓄えられるエネルギーと放出するエネルギーが等しいので,
\[
\begin{eqnarray}
EIT_{\mathrm {on}}&=&L\frac {\mathrm {d}i}{\mathrm {d}t}IT_{\mathrm {off}} \\[ 5pt ]
ET_{\mathrm {on}}&=&L\frac {\mathrm {d}i}{\mathrm {d}t}T_{\mathrm {off}} \\[ 5pt ]
L\frac {\mathrm {d}i}{\mathrm {d}t}&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}E \\[ 5pt ]
\end{eqnarray}
\]
となります。また回路方程式は,
\[
\begin{eqnarray}
E+L\frac {\mathrm {d}i}{\mathrm {d}t}&=&V_{\mathrm {o}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
E+L\frac {\mathrm {d}i}{\mathrm {d}t}&=&V_{\mathrm {o}} \\[ 5pt ]
E+\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}E&=&V_{\mathrm {o}} \\[ 5pt ]
V_{\mathrm {o}}&=&\frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}}E \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)問題のチョッパ回路が太陽光発電でよく用いられている理由
(ポイント)
・回路を見て昇圧チョッパであると判断できるので,\( \ V_{\mathrm {in}} < V_{\mathrm {out}} \ \)であることが分かります。
・太陽光発電は日射量により発電する電圧が変化するため,電圧を調整する必要があります。
・チョッパは直流の電圧を変圧するものなので,直並列した太陽電池の電圧を系統の電圧に合わせるためと記載すれば良いと思います。
(試験センター解答)
(例1)
入力\( \ V_{\mathrm {in}} \ \)よりも出力\( \ V_{\mathrm {out}} \ \)が大きい。太陽光発電で発電した直流電圧をより高い電圧のバッテリに充電するから。
(例2)
\( \ V_{\mathrm {in}} < V_{\mathrm {out}} \ \)である。系統の電圧波高値が太陽光発電の電圧よりも高いことがあるから。
(2)\( \ T_{\mathrm {on}} \ \)の時間におけるリアクトルの電圧\( \ v_{\mathrm {L}} \ \),電流\( \ i_{\mathrm {in}} \ \)は増加するか,減少するか
ワンポイント解説「1.昇圧チョッパ」の通り,\( \ T_{\mathrm {on}} \ \)の時間におけるリアクトルの電圧\( \ v_{\mathrm {L}} \ \)は,
\[
\begin{eqnarray}
v_{\mathrm {L}}&=&V_{\mathrm {in}}=L\frac {\mathrm {d}i_{\mathrm {in}}}{\mathrm {d}t} \\[ 5pt ]
\end{eqnarray}
\]
であり,上式より,\( \ \displaystyle \frac {\mathrm {d}i_{\mathrm {in}}}{\mathrm {d}t}>0 \ \)となるので,電流\( \ i_{\mathrm {in}} \ \)は徐々に増加する。
(3)\( \ T_{\mathrm {off}} \ \)の時間におけるリアクトルの電圧\( \ v_{\mathrm {L}} \ \),電流\( \ i_{\mathrm {in}} \ \)は増加するか,減少するか
ワンポイント解説「1.昇圧チョッパ」の通り,\( \ T_{\mathrm {off}} \ \)の時間におけるリアクトルの電圧\( \ v_{\mathrm {L}} \ \)は,
\[
\begin{eqnarray}
v_{\mathrm {L}}&=&V_{\mathrm {in}}-V_{\mathrm {out}}=L\frac {\mathrm {d}i_{\mathrm {in}}}{\mathrm {d}t} \\[ 5pt ]
\end{eqnarray}
\]
であり,上式において\( \ V_{\mathrm {in}}<V_{\mathrm {out}} \ \)であるから,\( \ \displaystyle \frac {\mathrm {d}i_{\mathrm {in}}}{\mathrm {d}t}<0 \ \)となるので,電流\( \ i_{\mathrm {in}} \ \)は徐々に減少する。
(4)ダイオード\( \ \mathrm {D} \ \)に流れる電流\( \ i_{\mathrm {D}} \ \)の平均値\( \ I_{\mathrm {D}} \ \)
ワンポイント解説「1.昇圧チョッパ」の通り,ダイオード\( \ \mathrm {D} \ \)を導通するのは\( \ T_{\mathrm {off}} \ \)の時間のみであり,題意よりその大きさは一定値\( \ I_{\mathrm {in}} \ \)である。したがって,ダイオード\( \ \mathrm {D} \ \)に流れる電流\( \ i_{\mathrm {D}} \ \)の平均値\( \ I_{\mathrm {D}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {D}}&=&\frac {T_{\mathrm {off}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}I_{\mathrm {in}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)出力電圧\( \ V_{\mathrm {out}} \ \)
ワンポイント解説「1.昇圧チョッパ」の通り,定常状態において蓄えられるエネルギーと放出するエネルギーが等しいので,
\[
\begin{eqnarray}
V_{\mathrm {in}}I_{\mathrm {in}}T_{\mathrm {on}}&=&-v_{\mathrm {L}}I_{\mathrm {in}}T_{\mathrm {off}} \\[ 5pt ]
V_{\mathrm {in}}T_{\mathrm {on}}&=&-v_{\mathrm {L}}T_{\mathrm {off}} \\[ 5pt ]
&=&-\left( V_{\mathrm {in}}-V_{\mathrm {out}}\right) T_{\mathrm {off}} \\[ 5pt ]
&=& -V_{\mathrm {in}}T_{\mathrm {off}}+V_{\mathrm {out}}T_{\mathrm {off}} \\[ 5pt ]
V_{\mathrm {out}}T_{\mathrm {off}}&=& V_{\mathrm {in}}T_{\mathrm {on}}+V_{\mathrm {in}}T_{\mathrm {off}} \\[ 5pt ]
&=& V_{\mathrm {in}}\left( T_{\mathrm {on}}+T_{\mathrm {off}}\right) \\[ 5pt ]
\frac {V_{\mathrm {out}}}{V_{\mathrm {in}}}&=& \frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}} \\[ 5pt ]
V_{\mathrm {out}}&=& \frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}}V_{\mathrm {in}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
※上式の第1式において\( \ -v_{\mathrm {L}} \ \)としているのは,\( \ T_{\mathrm {off}} \ \)の時リアクトルを電源と見立てるとリアクトルから出力側に電流が流れ,問題図の矢印の方向を正とすると負の値となるためです。計算ミス防止のためにも解答式は覚えておきましょう。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは