《理論》〈電気回路〉[H25:問3]変圧器のある交流回路に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，変圧器のある交流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。

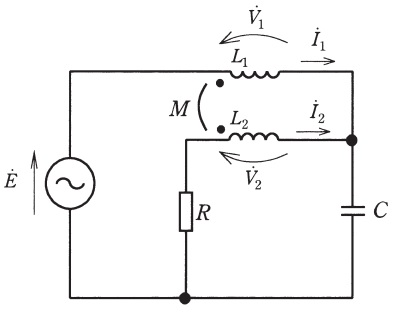
電圧が\( \ \dot E=E\left( 1+\mathrm {j}0\right) =E \ \)で，角周波数\( \ \omega \ \)(\( \ \omega ＞0 \ \))が可変の交流電源に，図のように，変圧器，静電容量\( \ C \ \)のコンデンサ，抵抗値が\( \ R \ \)の抵抗が接続されている。変圧器の一次側と二次側の自己インダクタンス及び相互インダクタンスは，それぞれ\( \ L_{1} \ \)，\( \ L_{2} \ \)，\( \ M \ \)(ただし\( \ L_{1}≠M \ \))で，極性は図のように定義する。

図中の電流\( \ {\dot I}_{1} \ \)，\( \ {\dot I}_{2} \ \)を用いて，電圧\( \ {\dot V}_{1} \ \)，\( \ {\dot V}_{2} \ \)を表すと，それぞれ\( \ {\dot V}_{1}=\fbox {　 （１） 　} \ \)，\( \ {\dot V}_{2}=\fbox {　 （２） 　} \ \)である。ここで，\( \ {\dot I}_{2}=0 \ \)となるように角周波数\( \ \omega \ \)を調整した場合，その角周波数は\( \ \fbox {　 （３） 　} \ \)で，そのときの\( \ {\dot I}_{1} \ \)は\( \ \fbox {　 （４） 　} \ \)であり，\( \ {\dot I}_{1} \ \)が電源電圧に対して遅れ位相となる条件は，\( \ \fbox {　 （５） 　} \ \)である。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {1}{\sqrt {MC}}　　　&（ロ）&　\mathrm {j}\frac {\sqrt{MC}}{M-L_{1}}E　　　&（ハ）&　\mathrm {j}\omega L_{1}{\dot I}_{1}+\mathrm {j}\omega M{\dot I}_{2} \\[ 5pt ] &（ニ）&　L_{1}＞M　　　&（ホ）&　\mathrm {j}\omega \left( L_{2}+M\right) {\dot I}_{1}　　　&（ヘ）&　\mathrm {j}\omega \left( L_{1}+M\right) {\dot I}_{1} \\[ 5pt ] &（ト）&　\frac {1}{RC}　　&（チ）&　L_{2}＞M　　　　&（リ）&　\frac {M}{R} \\[ 5pt ] &（ヌ）&　\sqrt {L_{1}L_{2}}＞M　　　&（ル）&　\mathrm {j}\omega M{\dot I}_{1}+\mathrm {j}\omega L_{2}{\dot I}_{2}　　　&（ヲ）&　\mathrm {j}\frac {RC}{M-L_{2}}E \\[ 5pt ] &（ワ）&　\mathrm {j}\omega \left( L_{2}+M\right) {\dot I}_{1}　　　&（カ）&　\mathrm {j}\frac {\sqrt{MC}}{L_{2}-L_{1}}E　　　&（ヨ）&　\mathrm {j}\omega \left( L_{1}+M\right) {\dot I}_{2} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

変圧器の和動接続もしくは差動接続を理解していることが前提で，その関係式の導出から回路計算をする問題です。後半の\( \ {\dot I}_{1} \ \)を求める計算が若干面倒ですが，二種だとこれぐらいの計算能力は必要であると考えて下さい。

1.変圧器の和動接続もしくは差動接続
変圧器は一次側及び二次側のコイルの巻き方や電流方向により，磁束を強め合う接続及び磁束を弱め合う接続方法があります。図1が磁束を強め合う接続方法で和動接続と呼ばれ，図2が磁束を弱め合う接続方法で差動接続と呼ばれます。それぞれの接続においての関係式は以下の通りとなります。

①和動接続
\[
\begin{eqnarray}
{\dot V}_{1}&=&\mathrm {j}\omega L_{1}{\dot I}_{1}+\mathrm {j}\omega M{\dot I}_{2} \\[ 5pt ] {\dot V}_{2}&=&\mathrm {j}\omega L_{2}{\dot I}_{2}+\mathrm {j}\omega M{\dot I}_{1} \\[ 5pt ] \end{eqnarray}
\]

②差動接続
\[
\begin{eqnarray}
{\dot V}_{1}&=&\mathrm {j}\omega L_{1}{\dot I}_{1}-\mathrm {j}\omega M{\dot I}_{2} \\[ 5pt ] {\dot V}_{2}&=&\mathrm {j}\omega L_{2}{\dot I}_{2}-\mathrm {j}\omega M{\dot I}_{1} \\[ 5pt ] \end{eqnarray}
\]

【解答】

(1)解答：ハ
(2)解答：ル
ワンポイント解説「1.変圧器の和動接続もしくは差動接続」の通り，問題図の回路は和動接続なので，
\[
\begin{eqnarray}
{\dot V}_{1}&=&\mathrm {j}\omega L_{1}{\dot I}_{1}+\mathrm {j}\omega M{\dot I}_{2} &　・・・・・・・・・・　①& \\[ 5pt ] {\dot V}_{2}&=&\mathrm {j}\omega L_{2}{\dot I}_{2}+\mathrm {j}\omega M{\dot I}_{1} &　・・・・・・・・・・　②& \\[ 5pt ] \end{eqnarray}
\] が成立する。

(3)解答：イ
\( \ {\dot I}_{2}=0 \ \)となるように角周波数\( \ \omega \ \)を調整するので，①及び②式は，
\[
\begin{eqnarray}
{\dot V}_{1}&=&\mathrm {j}\omega L_{1}{\dot I}_{1}　　　　　　　　 \ &　・・・・・・・・・・　①^{\prime }& \\[ 5pt ] {\dot V}_{2}&=&\mathrm {j}\omega M{\dot I}_{1}　　　　　　　　 \ &　・・・・・・・・・・　②^{\prime }& \\[ 5pt ] \end{eqnarray}
\] となる。また，問題図の閉回路においては，
\[
\begin{eqnarray}
\dot E&=&{\dot V}_{1}+\frac {1}{\mathrm {j}\omega C}{\dot I}_{1}　　　　　&　・・・・・・・・・・　③& \\[ 5pt ] \end{eqnarray}
\] 及び，
\[
\begin{eqnarray}
{\dot V}_{2}&=&-\frac {1}{\mathrm {j}\omega C}{\dot I}_{1}　　　　　　　 \ &　・・・・・・・・・・　④& \\[ 5pt ] \end{eqnarray}
\] の関係があるので，\( \ ②^{\prime } \ \)及び\( \ ④ \ \)から\( \ {\dot V}_{2} \ \)を消去すると，
\[
\begin{eqnarray}
\mathrm {j}\omega M{\dot I}_{1}&=&-\frac {1}{\mathrm {j}\omega C}{\dot I}_{1} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ \omega \ \)は，
\[
\begin{eqnarray}
\mathrm {j}\omega M{\dot I}_{1}&=&\mathrm {j}\frac {1}{\omega C}{\dot I}_{1} \\[ 5pt ] \omega M&=&\frac {1}{\omega C} \\[ 5pt ] \omega ^{2}&=&\frac {1}{MC} \\[ 5pt ] \omega &=&\frac {1}{\sqrt {MC}}　　　&　・・・・・・・・・・　⑤& \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ロ
\( \ ①^{\prime } \ \)を\( \ ③ \ \)に代入すると，
\[
\begin{eqnarray}
\dot E&=&\mathrm {j}\omega L_{1}{\dot I}_{1}　+\frac {1}{\mathrm {j}\omega C}{\dot I}_{1} \\[ 5pt ] \dot E&=&\mathrm {j}\left( \omega L_{1}-\frac {1}{\omega C}\right){\dot I}_{1} \\[ 5pt ] \end{eqnarray}
\] となり，これに\( \ ⑤ \)を代入すると，
\[
\begin{eqnarray}
\dot E&=&\mathrm {j}\left( \frac {1}{\sqrt {MC}} L_{1}-\frac {1}{\displaystyle \frac {1}{\sqrt {MC}} C}\right){\dot I}_{1} \\[ 5pt ] \dot E&=&\mathrm {j}\left( \frac {L_{1}}{\sqrt {MC}} -\frac {\sqrt {M}}{\sqrt {C} }\right){\dot I}_{1} \\[ 5pt ] \dot E&=&\mathrm {j}\left( \frac {L_{1}-M}{\sqrt {MC}} \right){\dot I}_{1}　　　&　・・・・・・・・・・　⑥& \\[ 5pt ] \end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
{\dot I}_{1}&=&\frac {1}{\mathrm {j}}\left( \frac {\sqrt {MC}}{L_{1}-M} \right) \dot E \\[ 5pt ] &=&-\mathrm {j}\frac {\sqrt {MC}}{L_{1}-M} \dot E \\[ 5pt ] &=&\mathrm {j}\frac {\sqrt {MC}}{M-L_{1}}\dot E \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ニ
\( \ {\dot I}_{1} \ \)が電源電圧に対して遅れ位相となるためには，\( \ ⑥ \)において，\( \ \displaystyle \frac {L_{1}-M}{\sqrt {MC}}＞0 \ \)が成立しなければならない。したがって，
\[
\begin{eqnarray}
\frac {L_{1}-M}{\sqrt {MC}}&＞&0 \\[ 5pt ] L_{1}-M&＞&0 \\[ 5pt ] L_{1}&＞&M \\[ 5pt ] \end{eqnarray}
\] と求められる。