《理論》〈電気及び電子計測〉[H27:問4]ホール測定に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，ホール測定に関する記述である。文中の$\fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$}$に当てはまる最も適切なものを解答群の中から選びなさい。

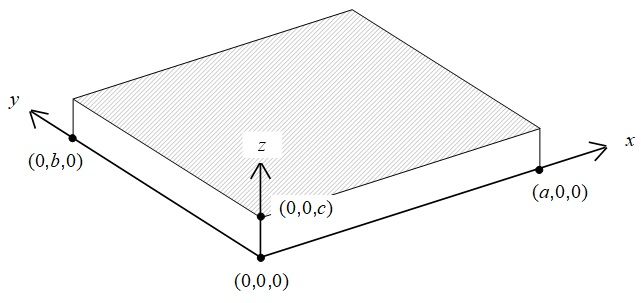
図のような，$x$方向に$a$，$y$方向に$b$，$z$方向に$c$の大きさをもった直方体の試料がある。ただし，試料は正孔がキャリヤの多数を占める$p$形半導体とする。

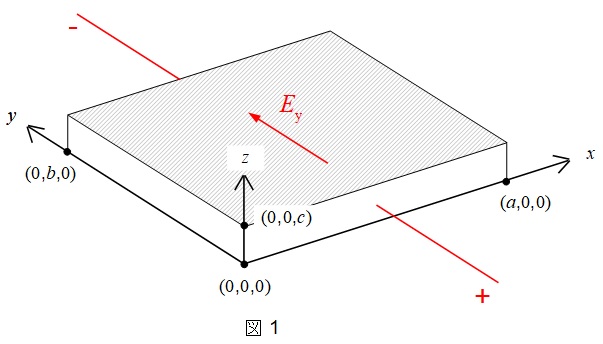
いま$y=0$の面が正に，$y=b$の面が負になるように電圧$V_{\mathrm {y}}$を掛けたとすると，一様な$y$方向の電界$E_{\mathrm {y}}$の大きさは$\fbox {　（１）　}$となり，電流が流れる。$y$方向のキャリヤの平均速度$v_{\mathrm {y}}$は，散乱がある半導体においては$v_{\mathrm {y}}=\mu E_{\mathrm {y}}$という比例関係が成り立つ。この$\mu $は$\fbox {　（２）　}$と呼ばれる。

ここで，垂直な$z$方向(図中で上向き)に磁束密度$B_{\mathrm {z}}$を加えると，磁界中を平均速度$v_{\mathrm {y}}$で$y$方向に動くキャリヤは，電荷量が単位電荷$q$であることから，$x$方向に大きさ$\fbox {　（３）　}$のローレンツ力$F_{\mathrm {L}}$を受ける。すると，$x=a$の面では正孔が溜まり，正に帯電し，$x=0$の面で正孔不足となり負に帯電して，$x$方向に電界$E_{\mathrm {x}}$が発生する。キャリヤが$x$方向の電界から受ける力$qE_{\mathrm {x}}$とローレンツ力$F_{\mathrm {L}}$は打ち消し合い，平衡状態となるので，$E_{\mathrm {x}}$の大きさは$\fbox {　（４）　}$となる。そこで$x=0$の面と$x=a$の面の間に発生する電圧$V_{\mathrm {H}}$と$y$方向に印加した電圧$V_{\mathrm {y}}$の比の大きさは$\fbox {　（５）　}$である。

以上の関係から磁束密度が分かっている場合には$\mu $を求めることができ，また$\mu $が分かった試料は，磁気センサとして用いることができる。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　\left| \mu E_{\mathrm {y}}B_{\mathrm {z}}\right|　　　&（ロ）&　\left| \frac {V_{\mathrm {y}}}{b}\right|　　　&（ハ）&　\left| q v_{\mathrm {y}}B_{\mathrm {z}}a\right| \\[ 5pt ] &（ニ）&　\left| \frac {\mu E_{\mathrm {y}}B_{\mathrm {z}}}{c}\right|　　　&（ホ）&　\left| \frac {\mu B_{\mathrm {z}}a}{b}\right|　　　&（ヘ）&　\left| q\mu E_{\mathrm {y}}B_{\mathrm {z}}\right| \\[ 5pt ] &（ト）&　\left| \frac {\mu B_{\mathrm {z}}}{c}\right|　　　&（チ）&　抵抗率　　　　&（リ）&　\left| q v_{\mathrm {y}}B_{\mathrm {z}}b\right| \\[ 5pt ] &（ヌ）&　伝導度　　　&（ル）&　\left| \frac {V_{\mathrm {H}}}{b}\right|　　　&（ヲ）&　\left| \frac {\mu E_{\mathrm {y}}B_{\mathrm {z}}}{a}\right| \\[ 5pt ] &（ワ）&　\left| \frac {V_{\mathrm {y}}}{a}\right|　　　&（カ）&　\left| \frac {\mu B_{\mathrm {z}}}{a}\right|　　　&（ヨ）&　移動度
\end{eqnarray}
\]

【ワンポイント解説】

ホール測定に関する問題となっていますが，中身はローレンツ力の計算に関する問題です。問題文を落ち着いて読み，確実に解答できるようにしましょう。

1.ローレンツ力
　磁束密度$B{[C]}$の磁界中において，$q\mathrm {[C]}$の電荷が，磁界と垂直方向に速度$v\mathrm {[m/s]}$で運動しているとき，電荷にかかるローレンツ力$F\mathrm {[N]}$は，
\[
F=qvB
\] となります。

【解答】

(1)解答：ロ
電圧$V_{\mathrm {y}}$により，$y$方向に一様な電界$E_{\mathrm {y}}$がかかったので，
\[
E_{\mathrm {y}}=\left| \frac {V_{\mathrm {y}}}{b}\right|
\] と求められる。

(2)解答：ヨ
$\mu $は移動度と呼ばれます。

(3)解答：ヘ
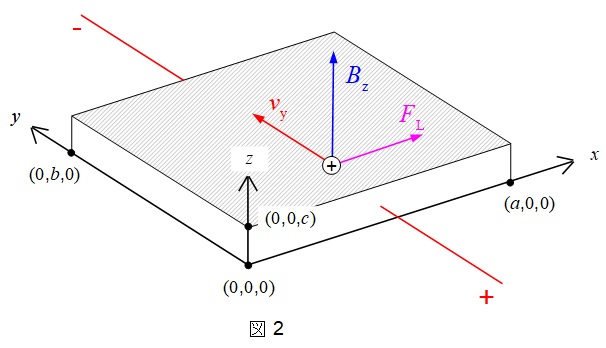
題意を図に示すと図2のようになる。ワンポイント解説「1.ローレンツ力」より，$x$方向のローレンツ力の大きさ$F_{\mathrm {L}}$は，
\[
\begin{eqnarray}
F_{\mathrm {L}}&=& \left| qv_{\mathrm {y}}B_{\mathrm {z}}\right| \\[ 5pt ] &=& \left| q\mu E_{\mathrm {y}}B_{\mathrm {z}}\right| \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：イ
平衡状態において,$x$方向の電界から受ける力$qE_{\mathrm {x}}$とローレンツ力$F_{\mathrm {L}}$は等しいので，
\[
\begin{eqnarray}
qE_{\mathrm {x}}&=& \left| q\mu E_{\mathrm {y}}B_{\mathrm {z}}\right| \\[ 5pt ] E_{\mathrm {x}}&=& \left| \mu E_{\mathrm {y}}B_{\mathrm {z}}\right| \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ホ
$x=0$の面と$x=a$の面の間に発生する電圧$V_{\mathrm {H}}$の大きさは，
\[
\begin{eqnarray}
V_{\mathrm {H}}&=& E_{\mathrm {x}}a \\[ 5pt ] &=& \left| \mu E_{\mathrm {y}}B_{\mathrm {z}}a\right| \\[ 5pt ] &=& \left| \mu \frac { V_{\mathrm {y}}}{b}B_{\mathrm {z}}a\right| \\[ 5pt ] &=& \left| \frac {\mu B_{\mathrm {z}}a}{b} V_{\mathrm {y}}\right| \\[ 5pt ] \end{eqnarray}
\] となるので，$V_{\mathrm {H}}$と$V_{\mathrm {y}}$の比の大きさは，
\[
\frac {V_{\mathrm {H}}}{V_{\mathrm {y}}}= \left| \frac {\mu B_{\mathrm {z}}a}{b} \right|
\] と求められる。