《理論》〈電気回路〉[H30:問6]交流回路のアドミタンスに関する計算問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，交流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

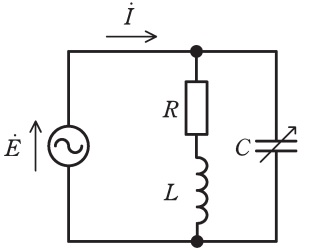
図の回路において，キャパシタ\( \ C \ \)のみが可変であり，電圧\( \ \dot E \ \)の角周波数は\( \ \omega \ \)である。

電源からみた回路の合成アドミタンスは，\( \ \dot Y= \ \fbox {　 （１） 　} \ +\mathrm {j} \ \fbox {　 （２） 　} \ \)であり，可変キャパシタ\( \ C=\fbox {　 （３） 　} \ \)のとき，電圧\( \ \dot E \ \)と電流\( \ \dot I \ \)の位相差は\( \ \displaystyle \frac {\pi }{4} \ \mathrm {rad} \ \)となる。

また，可変キャパシタ\( \ C=\fbox {　 （４） 　} \ \)のとき，回路の合成アドミタンス\( \ \dot Y \ \)の大きさ\( \ \left| \dot Y\right| \ \)が最小となる。このとき，電圧\( \ \dot E \ \)と電流\( \ \dot I \ \)の位相の関係は，\( \ \fbox {　 （５） 　} \ \)となる。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {\omega L}{R^{2}+\omega ^{2}L^{2}}　　　&（ロ）&　\omega \left( C-\frac {L}{R^{2}+\omega ^{2}L^{2}}\right)　　　&（ハ）&　\frac {R+\omega L}{\omega \left( R^{2}+\omega ^{2}L^{2}\right) } \\[ 5pt ] &（ニ）&　\frac {1}{\omega C\left( R^{2}+\omega ^{2}L^{2}\right) }　　　&（ホ）&　\omega \left( C-\frac {R}{R^{2}+\omega ^{2}L^{2}}\right)　　　&（ヘ）&　\omega \left[ L-\frac {1}{C \left( R^{2}+\omega ^{2}L^{2}\right) }\right] \\[ 5pt ] &（ト）&　\frac {1}{\omega \left( R^{2}+\omega ^{2}L^{2}\right) }　　　&（チ）&　\frac {L}{R^{2}+\omega ^{2}L^{2}}　　　　&（リ）&　\frac {R}{R^{2}+\omega ^{2}L^{2}} \\[ 5pt ] &（ヌ）&　\frac {R}{R+\omega L}　　　&（ル）&　\frac {1}{C \left( R^{2}+\omega ^{2}L^{2}\right) }　　　&（ヲ）&　\frac {R}{\omega \left( R^{2}+\omega ^{2}L^{2}\right) } \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
&（ワ）&　電圧が電流に対して進み　　　　　　　　　　　&（カ）&　電圧と電流が同相 \\[ 5pt ] &（ヨ）&　電圧が電流に対して遅れ &&\\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

合成アドミタンス（インピーダンスの逆数）の導出から，可変キャパシタの値の導出をする問題です。電験三種でもB問題ぐらいになると出題されたのではないかというレベル感に感じると思います。

【解答】

(1)解答：リ
(2)解答：ロ
\( \ R \ \)と\( \ L \ \)の合成インピーダンス\( \ \dot Z \ \)は，
\[
\begin{eqnarray}
\dot Z&=&R+\mathrm {j}\omega L \\[ 5pt ] \end{eqnarray}
\] であるから，電源からみた回路の合成アドミタンス\( \ \dot Y \ \)は，
\[
\begin{eqnarray}
\dot Y&=&\frac {1}{\dot Z}+\mathrm {j}\omega C \\[ 5pt ] &=&\frac {1}{R+\mathrm {j}\omega L}+\mathrm {j}\omega C \\[ 5pt ] &=&\frac {1}{R+\mathrm {j}\omega L}\times \frac {R-\mathrm {j}\omega L}{R-\mathrm {j}\omega L}+\mathrm {j}\omega C \\[ 5pt ] &=&\frac {R-\mathrm {j}\omega L}{R^{2}+\omega ^{2}L^{2}}+\mathrm {j}\omega C \\[ 5pt ] &=&\frac {R}{R^{2}+\omega ^{2}L^{2}}+\mathrm {j}\left( \omega C-\frac {\omega L}{R^{2}+\omega ^{2}L^{2}}\right) \\[ 5pt ] &=&\frac {R}{R^{2}+\omega ^{2}L^{2}}+\mathrm {j}\omega \left( C-\frac {L}{R^{2}+\omega ^{2}L^{2}}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ハ
題意より電圧\( \ \dot E \ \)と電流\( \ \dot I \ \)の位相差が\( \ \displaystyle \frac {\pi }{4} \ \mathrm {rad} \ \)であるから，\( \ \dot I=\dot Y\dot E \ \)の関係より，\( \ \dot Y \ \)の実部と虚部の大きさが等しければ良いことになる。したがって，
\[
\begin{eqnarray}
\frac {R}{R^{2}+\omega ^{2}L^{2}}&=&\omega \left( C-\frac {L}{R^{2}+\omega ^{2}L^{2}}\right) \\[ 5pt ] \frac {R}{R^{2}+\omega ^{2}L^{2}}+\frac {\omega L}{R^{2}+\omega ^{2}L^{2}}&=&\omega C \\[ 5pt ] C&=&\frac {1}{\omega }\left( \frac {R+\omega L}{R^{2}+\omega ^{2}L^{2}}\right) \\[ 5pt ] C&=&\frac {R+\omega L}{\omega \left( R^{2}+\omega ^{2}L^{2}\right) } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：チ
回路の合成アドミタンス\( \ \dot Y \ \)の大きさ\( \ \left| \dot Y\right| \ \)が最小となるのは虚部が零の時であるため，
\[
\begin{eqnarray}
C-\frac {L}{R^{2}+\omega ^{2}L^{2}}&=&0 \\[ 5pt ] C&=&\frac {L}{R^{2}+\omega ^{2}L^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：カ
合成アドミタンス\( \ \dot Y \ \)が実部のみとなるため，電圧と電流の位相は等しくなる。