《電力》〈水力〉[H18:問12]水管内を流れる流水の流速と圧力に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

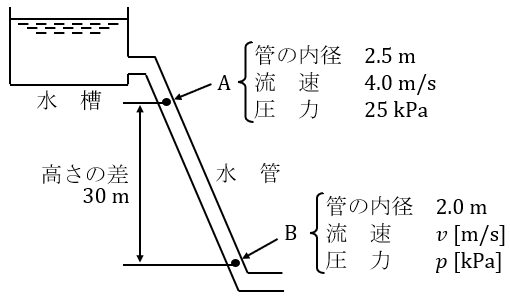
図の水管内を水が充満して流れている。点\( \ \mathrm {A} \ \)では管の内径\( \ 2.5 \ \mathrm {[m]} \ \)で，これより\( \ 30 \ \mathrm {[m]} \ \)低い位置にある点\( \ \mathrm {B} \ \)では内径\( \ 2.0 \ \mathrm {[m]} \ \)である。点\( \ \mathrm {A} \ \)では流速\( \ 4.0 \ \mathrm {[m / s]} \ \)で圧力は\( \ 25 \ \mathrm {[kPa]} \ \)と計測されている。このときの点\( \ \mathrm {B} \ \)における流速\( \ v \ \mathrm {[m / s]} \ \)と圧力\( \ p \ \mathrm {[kPa]} \ \)に最も近い値を組み合わせたのは次のうちどれか。

なお，圧力は水面との圧力差とし，水の密度は\( \ 1.0\times 10^{3} \ \mathrm {[kg / m^{3}]} \ \)とする。

\[
\begin{array}{ccc}
& 流速 \ v \ \mathrm {[m / s]} \ 　 & 　圧力 \ p \ \mathrm {[kPa]} \ 　\\
\hline
(1) & 　4.0　 & 　296　 \\
\hline
(2) & 　5.0　 & 　296　 \\
\hline
(3) & 　5.0　 & 　307　 \\
\hline
(4) & 　6.3　 & 　307　 \\
\hline
(5) & 　6.3　 & 　319　 \\
\hline
\end{array}
\]

【ワンポイント解説】

連続の定理とベルヌーイの定理を用いた問題です。
ベルヌーイの定理は与えられることも多い公式ですが，本問では与えられていないので，覚えておく必要があります。

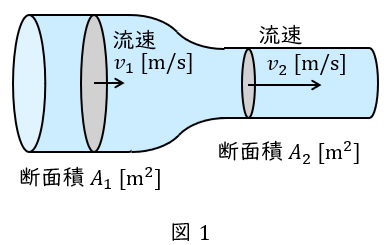
1.断面積\( \ A \ \mathrm {[m^{2}]} \ \)と流速\( \ v \ \mathrm {[m / s ]} \ \)と流量\( \ Q \ \mathrm {[m^{3} / s ]} \ \)の関係
断面積\( \ A \ \mathrm {[m^{2}]} \ \)の配管内を流速\( \ v \ \mathrm {[m / s ]} \ \)で水が流れている時，配管内を流れる水の流量\( \ Q \ \mathrm {[m^{3} / s ]} \ \)は，
\[
\begin{eqnarray}
Q&=&Av \\[ 5pt ] \end{eqnarray}
\] となり，図1のように配管の断面積が変化するとき，
\[
\begin{eqnarray}
A_{1}v_{1}&=&A_{2}v_{2} \\[ 5pt ] \end{eqnarray}
\] が成立し，これを連続の定理といいます。

2.ベルヌーイの定理
位置水頭が\( \ h \ \mathrm {[m]} \ \)，圧力水頭が\( \ \displaystyle \frac {p}{\rho g} \ \mathrm {[m]} \ \)，速度水頭が\( \ \displaystyle \frac {v^{2}}{2g} \ \mathrm {[m]} \ \)で表されるとき，これらの総和はエネルギー保存則によりどの場所でも等しくなります。
\[
\begin{eqnarray}
h+\frac {p}{\rho g}+\frac {v^{2}}{2g}&=&一定 \\[ 5pt ] \end{eqnarray}
\]

【解答】

解答：(4)
断面\( \ \mathrm {A} \ \)の断面積\( \ S_{\mathrm {A}} \ \mathrm {[m^{2}]} \ \)は，内径が\( \ 2.5 \ \mathrm {m} \ \)であるから，
\[
\begin{eqnarray}
S_{\mathrm {A}}&=&\pi \left( \frac {2.5}{2}\right) ^{2} \\[ 5pt ] &≒&4.909 \ \mathrm {[m^{2}]} \\[ 5pt ] \end{eqnarray}
\] であり，同様に，断面\( \ \mathrm {B} \ \)の断面積\( \ S_{\mathrm {B}} \ \mathrm {[m^{2}]} \ \)は，内径が\( \ 2.0 \ \mathrm {m} \ \)であるから，
\[
\begin{eqnarray}
S_{\mathrm {B}}&=&\pi \left( \frac {2.0}{2}\right) ^{2} \\[ 5pt ] &≒&3.142 \ \mathrm {[m^{2}]} \\[ 5pt ] \end{eqnarray}
\] である。ワンポイント解説「1.断面積\( \ A \ \mathrm {[m^{2}]} \ \)と流速\( \ v \ \mathrm {[m / s ]} \ \)と流量\( \ Q \ \mathrm {[m^{3} / s ]} \ \)の関係」の通り，断面\( \ \mathrm {A} \ \)及び断面\( \ \mathrm {B} \ \)での流量が等しいことから，断面\( \ \mathrm {A} \ \)での流速\( \ v_{\mathrm {A}}=4.0 \ \mathrm {[m / s ]} \ \)とすると，
\[
\begin{eqnarray}
S_{\mathrm {A}}v_{\mathrm {A}}&=&S_{\mathrm {B}}v \\[ 5pt ] 4.909\times 4.0&=&3.142v \\[ 5pt ] v&≒&6.250　→　6.3 \ \mathrm {[m / s ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。断面\( \ \mathrm {B} \ \)を基準の高さとすると，ワンポイント解説「2.ベルヌーイの定理」より，
\[
\begin{eqnarray}
h_{\mathrm {A}}+\frac {p_{\mathrm {A}}}{\rho g}+\frac {v_{\mathrm {A}}^{2}}{2g}&=&h_{\mathrm {B}}+\frac {p}{\rho g}+\frac {v^{2}}{2g} \\[ 5pt ] 30+\frac {25\times 10^{3}}{1 \ 000 \times 9.8}+\frac {4.0^{2}}{2\times 9.8}&=&0+\frac {p}{1 \ 000 \times 9.8}+\frac {6.250^{2}}{2\times 9.8} \\[ 5pt ] \frac {p}{1 \ 000 \times 9.8}&=&30+\frac {25\times 10^{3}}{1 \ 000 \times 9.8}+\frac {4.0^{2}}{2\times 9.8}-\frac {6.250^{2}}{2\times 9.8} \\[ 5pt ] p&=&\left( 1 \ 000 \times 9.8\right)\times \left( 30+\frac {25\times 10^{3}}{1 \ 000 \times 9.8}+\frac {4.0^{2}}{2\times 9.8}-\frac {6.250^{2}}{2\times 9.8}\right) \\[ 5pt ] &=&30\times 1 \ 000 \times 9.8+25\times 10^{3}+\frac {4.0^{2}}{2}\times 1 \ 000-\frac {6.250^{2}}{2}\times 1 \ 000 \\[ 5pt ] &≒&294 \ 000+25 \ 000+8 \ 000-19 \ 531 \\[ 5pt ] &≒&307 \ 000 \ \mathrm {[Pa]}　→　307 \ \mathrm {[kPa]} \\[ 5pt ] \end{eqnarray}
\] と求められる。