《電力》〈送電〉[H25:問16]架空送電線路の力率計算に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

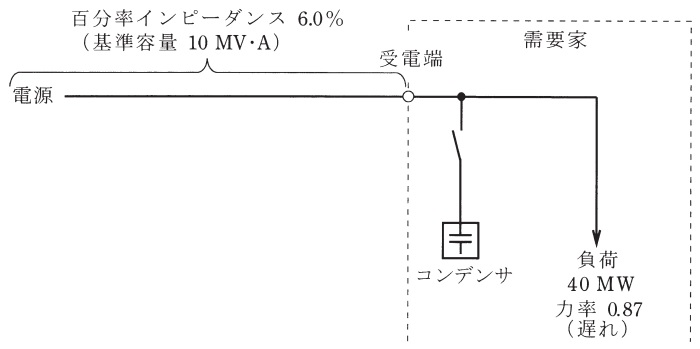
図のように，特別高圧三相\( \ 3 \ \)線式\( \ 1 \ \)回線の専用架空送電線路で受電している需要家がある。需要家の負荷は，\( \ 40 \ \mathrm {[MW]} \ \)，力率が遅れ\( \ 0.87 \ \)で，需要家の受電端電圧は\( \ 66 \ \mathrm {[kV]} \ \)である。

ただし，需要家から電源側をみた電源と専用架空送電線路を含めた百分率インピーダンスは，基準容量\( \ 10 \ \mathrm {[MV\cdot A]} \ \)あたり\( \ 6.0 \ \mathrm {[％]} \ \)とし，抵抗はリアクタンスに比べ非常に小さいものとする。その他の定数や条件は無視する。

次の(a)及び(b)の問に答えよ。

(a)　需要家が受電端において，力率\( \ 1 \ \)の受電になるために必要なコンデンサの総容量\( \ \mathrm {[Mvar]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。
ただし，受電端電圧は変化しないものとする。

　(1)　\( \ 9.7 \ \)　　(2)　\( \ 19.7 \ \)　　(3)　\( \ 22.7 \ \)　　(4)　\( \ 34.8 \ \)　　(5)　\( \ 81.1 \ \)

(b)　需要家のコンデンサが開閉動作を伴うとき，受電端の電圧変動率を\( \ 2.0 \ \mathrm {[％]} \ \)以内にするために必要なコンデンサ単機容量\( \ \mathrm {[Mvar]} \ \)の最大値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 0.46 \ \)　　(2)　\( \ 1.9 \ \)　　(3)　\( \ 3.3 \ \)　　(4)　\( \ 4.3 \ \)　　(5)　\( \ 5.7 \ \)

【ワンポイント解説】

(a)はベクトル図を描いてイメージできればそれほど難しい問題ではありません。(b)は若干ひねりのきいた問題と言えると思います。百分率インピーダンスからオーム値の導出は必須となりますので，試験までには理解しておくようにしましょう。

1.電圧変動率\( \ \varepsilon \ \)の定義
基準電圧を\( \ V_{\mathrm {n}} \ \)とした時，電圧が\( \ V^{\prime } \ \)に変動した時の電圧変動率\( \ \varepsilon \ \)は，
\[
\begin{eqnarray}
\varepsilon &=&\frac {V^{\prime }-V_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となります。

2.オーム法からパーセントインピーダンス法への変換
基準容量を\( \ P_{\mathrm {n}} \ \)，基準電圧を\( \ V_{\mathrm {n}} \ \)，基準電流を\( \ I_{\mathrm {n}} \ \)とすると，
\[
\begin{eqnarray}
％Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 (定義) \\[ 5pt ] &=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ] &=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] &=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100　　 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(3)
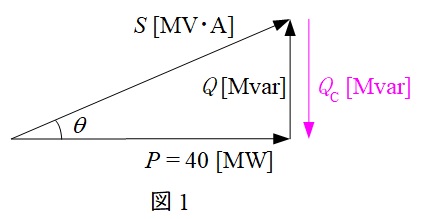
コンデンサを投入することによって，力率が\( \ 1 \ \)すなわち無効電力が\( \ 0 \ \)となるから，題意に沿って，受電端側のベクトル図を描くと図1のようになる。
図1より負荷の無効電力の大きさ\( \ Q \ \)がコンデンサ総容量\( \ Q_{\mathrm {C}} \ \)と等しいから，コンデンサ総容量\( \ Q_{\mathrm {C}} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {C}}&=&Q \\[ 5pt ] &=&S\sin \theta \\[ 5pt ] &=&\frac {P}{\cos \theta }\sin \theta \\[ 5pt ] &=&\frac {P}{\cos \theta }\sqrt {1-\cos ^{2}\theta } \\[ 5pt ] &=&\frac {40}{0.87}\sqrt {1-0.87^{2}} \\[ 5pt ] &≒&22.7 \ \mathrm {[Mvar]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
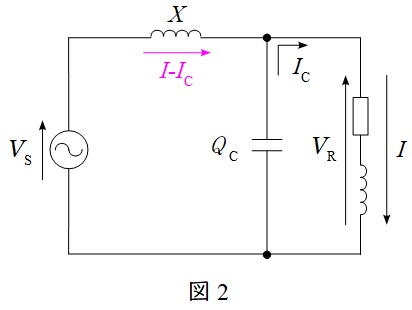
コンデンサ投入時の\( \ 1 \ \)相分等価回路は図2のようになる。
ここで，電圧変動率\( \ \varepsilon \ \)が\( \ 2.0 \ \mathrm {[％]} \ \)であるから，コンデンサ投入後の電圧を\( \ V_{\mathrm {R}} \ \)，基準電圧\( \ V_{\mathrm {n}}=66 \ \mathrm {[kV]} \ \)とすると，
\[
\begin{eqnarray}
\varepsilon &=&\frac {V_{\mathrm {R}}-V_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ] 2.0 &=&\frac {V_{\mathrm {R}}-66}{66}\times 100 \\[ 5pt ] V_{\mathrm {R}} &=&67.32 \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
\] となる。また，ワンポイント解説「2.オーム法からパーセントインピーダンス法への変換」より，送電線のリアクタンスをオーム値に変換すると，
\[
\begin{eqnarray}
％X&=&\frac {P_{\mathrm {n}}X}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] 6.0&=&\frac {10\times 10^{6}X}{\left( 66\times 10^{3}\right) ^{2}}\times 100 \\[ 5pt ] X&≒&26.14 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。コンデンサ接続前後にて，送電線に流れる電流が\( \ I \ \)→\( \ I-I_{\mathrm {C}} \ \)に変化するので，それぞれの受電電圧について方程式を立てると，
\[
\begin{eqnarray}
V_{\mathrm {n}}&=&V_{\mathrm {S}}-\sqrt {3}XI　&・・・・・・・・・①& \\[ 5pt ] V_{\mathrm {R}}&=&V_{\mathrm {S}}-\sqrt {3}X\left( I-I_{\mathrm {C}}\right)　&・・・・・・・・・②& \\[ 5pt ] \end{eqnarray}
\] となり，\(①-②\)により，
\[
\begin{eqnarray}
V_{\mathrm {n}}-V_{\mathrm {R}}&=&-\sqrt {3}XI_{\mathrm {C}} \\[ 5pt ] I_{\mathrm {C}}&=&\frac {V_{\mathrm {R}}-V_{\mathrm {n}}}{\sqrt {3}X} \\[ 5pt ] &=&\frac {67.32\times 10^{3}-66\times 10^{3}}{\sqrt {3}\times 26.14} \\[ 5pt ] &≒&29.15 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められるので，コンデンサ容量\( \ Q_{\mathrm {C}} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {C}}&=&\sqrt {3}V_{\mathrm {n}}I_{\mathrm {C}} \\[ 5pt ] &=&\sqrt {3}\times 66\times 10^{3}\times 29.15 \\[ 5pt ] &≒&3300000 \ \mathrm {[var]}　→　3.3 \ \mathrm {[Mvar]} \\[ 5pt ] \end{eqnarray}
\] と求められる。