《電力》〈送電〉[H27:問10]ケーブルの誘電体損に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

電圧\(\mathrm {66kV}\)，周波数\(\mathrm {50Hz}\)，こう長\(\mathrm {5km}\)の交流三相3線式地中電線路がある。ケーブルの心線1線当たりの静電容量が\(\mathrm {0.43\mu F /km}\)，誘電正接が\(0.03％\)であるとき，このケーブル心線3線合計の誘電体損の値\(\mathrm {[W]}\)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(141\)　　(2)　\(294\)　　(3)　\(883\)　　(4)　\(1324\)　　(5)　\(2648\)

【ワンポイント解説】

誘電体損の公式を暗記していれば，与えられた数字だけで解くことができますが，できれば，その公式に至るプロセスも本問で理解しておきたいところです。

1.ケーブルの誘電体損\(W_{\mathrm {d}}\)
角周波数を\(\omega \)，周波数を\(f\)，静電容量を\(C\)，誘電正接を\(\tan \delta \)とした時，誘電体損\(W_{\mathrm {d}}\)は，
\[
\begin{eqnarray}
W_{\mathrm {d}} &=&\omega CV^{2}\tan \delta \\[ 5pt ] &=&2\pi f CV^{2}\tan \delta \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(3)
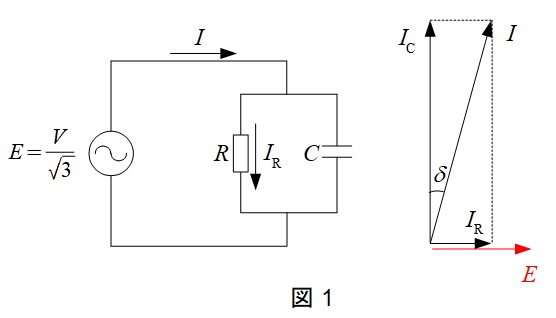
題意に沿って，一相分の等価回路とベクトル図を描くと図1の通りとなる。
図1より，コンデンサに流れる電流の大きさ\(I_{\mathrm {C}}\)は，
\[
\begin{eqnarray}
I_{\mathrm {C}} &=&\omega C\frac {V}{\sqrt {3}} \\[ 5pt ] &=&\frac {\omega CV}{\sqrt {3}} \\[ 5pt ] \end{eqnarray}
\] となる。また，ベクトル図より，抵抗を流れる電流の大きさ\(I_{\mathrm {R}}\)は，
\[
\begin{eqnarray}
I_{\mathrm {R}} &=&I_{\mathrm {C}}\tan \delta \\[ 5pt ] &=&\frac {\omega CV}{\sqrt {3}}\tan \delta \\[ 5pt ] \end{eqnarray}
\] となる。よって，3線合計の誘電体損\(W_{\mathrm {d}}\)は，
\[
\begin{eqnarray}
W_{\mathrm {d}} &=&3\times \frac {V}{\sqrt {3}} I_{\mathrm {R}} \\[ 5pt ] &=&3\times \frac {V}{\sqrt {3}} \frac {\omega CV}{\sqrt {3}}\tan \delta \\[ 5pt ] &=&\omega CV^{2}\tan \delta \\[ 5pt ] &=&2\pi f CV^{2}\tan \delta \\[ 5pt ] \end{eqnarray}
\] と求められる。ここで，
\[
\begin{eqnarray}
C &=&0.43\times 10^{-6}\times 5 \\[ 5pt ] &=&2.15\times 10^{-6} \ \mathrm {[F]} \\[ 5pt ] \end{eqnarray}
\] であるから，各値を代入すると，
\[
\begin{eqnarray}
W_{\mathrm {d}} &=&2\pi f CV^{2}\tan \delta \\[ 5pt ] &=&2\pi \times 50\times 2.15\times 10^{-6} \times (66\times 10^{3} ) ^{2} \times 0.0003 \\[ 5pt ] &≒&883 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。