《電力》〈送電〉[H27:問17]電力系統の送電電力に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

図に示すように，線路インピーダンスが異なる\(\mathrm {A}\)，\(\mathrm {B}\)回線で構成される\(\mathrm {154 \ kV}\)系統があったとする。\(\mathrm {A}\)回線側にリアクタンス\(\mathrm {5％}\)の直列コンデンサが設置されているとき，次の(a)及び(b)の問に答えよ。なお，系統の基準容量は，\(\mathrm {10 \ MV\cdot A}\)とする。

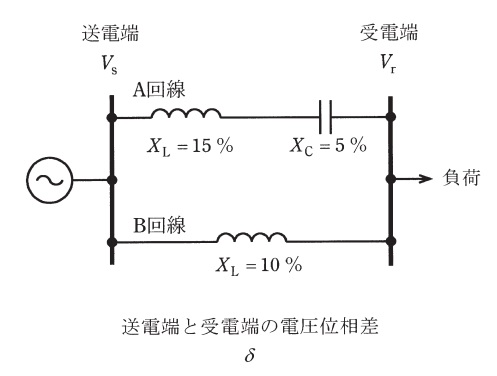
(a)　図に示す系統の合成線路インピーダンスの値\(\mathrm {[％]}\)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 3.3 \ \)　　(2)　\( \ 5.0 \ \)　　(3)　\( \ 6.0 \ \)　　(4)　\( \ 20.0 \ \)　　(5)　\( \ 30.0 \ \)

(b)　送電端と受電端の電圧位相差\(\delta \)が30度であるとき，この系統での送電電力\(P\)の値\(\mathrm {[MW]}\)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　　ただし，送電端電圧\(V_{\mathrm {s}}\)，受電端電圧\(V_{\mathrm {r}}\)は，それぞれ\(\mathrm {154 \ kV}\)とする。

　(1)　\( \ 17 \ \)　　(2)　\( \ 25 \ \)　　(3)　\( \ 83 \ \)　　(4)　\( \ 100 \ \)　　(5)　\( \ 152 \ \)

【ワンポイント解説】

(a)の合成インピーダンスの計算は通常のオーム法と同じように計算できます。(b)はパーセントインピーダンスからオームへの変換と送電電力の公式を理解しているかどうかを問う問題で，いずれも重要な公式となるので，理解しておくようにしておきましょう。

1.パーセントインピーダンス
基準容量\(P_{\mathrm {B}}\)，基準電圧\(V_{\mathrm {B}}\)，基準電流\(I_{\mathrm {B}}\)，基準インピーダンス\(Z_{\mathrm {B}}\)とすると，
\[
\begin{eqnarray}
％Z&=&\frac {Z\left[ \Omega \right] }{Z_{\mathrm {B}}}\times 100 \\[ 5pt ] &=&\frac {Z\left[ \Omega \right] P_{\mathrm {B}}}{V_{\mathrm {B}}^{2}}\times 100 \\[ 5pt ] \end{eqnarray}
\] \[
\left( ∵Z_{\mathrm {B}}=\frac {\displaystyle \frac {V_{\mathrm {B}}}{\sqrt {3}}}{I_{\mathrm {B}}}=\frac {\displaystyle \frac {V_{\mathrm {B}}}{\sqrt {3}}}{\displaystyle \frac {P_{\mathrm {B}}}{\sqrt {3} V_{\mathrm {B}}}}=\frac {V_{\mathrm {B}}^{2}}{P_{\mathrm {B}}}\right)
\] となります。

2.送電線の送電電力\(P\)
送電端電圧\(V_{\mathrm {s}}\)，受電端電圧\(V_{\mathrm {r}}\)，送電端と受電端電圧の相差角\(\delta \)，線路のリアクタンス\(X\)とした時，送電電力\(P\)は，
\[
P=\frac {V_{\mathrm {s}}V_{\mathrm {r}}}{X}\sin \delta
\] となります。

【解答】

(a)解答：(2)
\(\mathrm {A}\)回線の合成インピーダンス\(X_{\mathrm {A}}\)は，
\[
\begin{eqnarray}
X_{\mathrm {A}}&=&X_{\mathrm {L}}-X_{\mathrm {C}} \\[ 5pt ] &=&15-5 \\[ 5pt ] &=&10 \ \mathrm {[％ ]}\\[ 5pt ] \end{eqnarray}
\] である。\(\mathrm {A}\)回線と\(\mathrm {B}\)回線の並列合成インピーダンス\(％X\)は，
\[
\begin{eqnarray}
％X&=&\frac {X_{\mathrm {A}}X_{\mathrm {L}}}{X_{\mathrm {A}}+X_{\mathrm {L}}} \\[ 5pt ] &=&\frac {10\times 10}{10+10} \\[ 5pt ] &=&5 \ \mathrm {[％ ]}\\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
ワンポイント解説「1.パーセントインピーダンス」より，線路の合成抵抗\(X\)は，
\[
\begin{eqnarray}
％X&=&\frac {X P_{\mathrm {B}}}{V_{\mathrm {B}}^{2}}\times 100 \\[ 5pt ] 5&=&\frac {X \times 10\times 10^{6}}{(154\times 10^{3})^{2}}\times 100 \\[ 5pt ] X&=&118.58 \ \mathrm {[\Omega ]}\\[ 5pt ] \end{eqnarray}
\] であるので，ワンポイント解説「2.送電線の送電電力\(P\)」の通り，送電電力\(P\)は，
\[
\begin{eqnarray}
P&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}}{X}\sin \delta\\[ 5pt ] &=&\frac {154\times 10^{3}\times 154\times 10^{3}}{118.58}\sin 30° \\[ 5pt ] &=&100\times 10^{6} \ \mathrm {[W]}　→　100 \ \mathrm {[MW]}\\[ 5pt ] \end{eqnarray}
\] と求められる。