《電力》〈送電〉[H30:問17]百分率インピーダンスと送電電力に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

図のように，抵抗を無視できる一回線短距離送電線路のリアクタンスと送電電力について，次の(a)及び(b)の問に答えよ。ただし，一相分のリアクタンス\( \ X =11 \ \mathrm {\Omega } \ \)，受電端電圧\( \ V_{\mathrm {r}} \ \)は\( \ 66 \ \mathrm {kV} \ \)で常に一定とする。

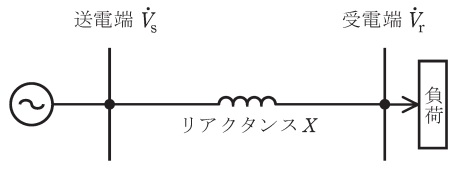
(a)　基準容量を\( \ 100 \ \mathrm {MV \cdot A} \ \)，基準電圧を受電端電圧\( \ V_{\mathrm {r}} \ \)としたときの送電線路のリアクタンスをパーセント法で示した値\(\mathrm {[％]}\)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(0.4\)　　(2)　\(2.5\)　　(3)　\(25\)　　(4)　\(40\)　　(5)　\(400\)

(b)　送電電圧\( \ V_{\mathrm {s}} \ \)を\( \ 66 \ \mathrm {kV} \ \)，相差角(送電端電圧\( \ {\dot V}_{\mathrm {s}} \ \)と受電端電圧\( \ {\dot V}_{\mathrm {r}} \ \)の位相差)\( \ \delta \ \)を\( \ 30°
\ \)としたとき，送電電力\( \ P_{\mathrm {s}} \ \)の値\(\mathrm {[MW]}\)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(22\)　　(2)　\(40\)　　(3)　\(198\)　　(4)　\(343\)　　(5)　\(3960\)

【ワンポイント解説】

本問はきちんと公式が頭の中に入っていれば解ける問題で，近年のB問題としてはかなり易しい問題と言えます。本問で使用する公式は非常に重要な公式なので，必ず暗記しておくようにしておきましょう。

1.オーム法からパーセントインピーダンス法への抵抗値の変換
パーセントインピーダンスは基準容量，基準電圧を定めた定義なので，ある程度公式を暗記する必要があります。
基準容量を\( \ P_{\mathrm {n}} \ \)，基準電圧を\( \ V_{\mathrm {n}} \ \)，基準電流を\( \ I_{\mathrm {n}} \ \)とすると，
\[
\begin{eqnarray}
％Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 (定義) \\[ 5pt ] &=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ] &=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] &=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100　　 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ] \end{eqnarray}
\]

2.送電線の送電電力
送電電力の公式は非常に重要な公式で確実に暗記しておく必要がありますが，その導出は一種レベルになりますので，三種の受験としては暗記しておくようにして下さい。
送電端電圧を\( \ V_{\mathrm {s}} \ \)，受電端電圧を\( \ V_{\mathrm {r}} \ \)，送電線路のリアクタンスを\( \ X \ \)，\( \ V_{\mathrm {s}} \ \)と\( \ V_{\mathrm {r}} \ \)の相差角を\(\delta \)とすると，送電電力\(P\)は，
\[
\begin{eqnarray}
P&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}}{X}\sin \delta \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

(a)解答：(3)
ワンポイント解説「1.オーム法からパーセントインピーダンス法への抵抗値の変換」より，送電線のリアクタンスのパーセントインピーダンス\(％X\)は，
\[
\begin{eqnarray}
％X&=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100　\\[ 5pt ] &=&\frac {100 \times 10^{6}\times 11}{\left( 66 \times 10^{3} \right) ^{2}}\times 100　\\[ 5pt ] &≒&25 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
ワンポイント解説「2.送電線の送電電力」より，
\[
\begin{eqnarray}
P_{\mathrm {s}}&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}}{X}\sin \delta \\[ 5pt ] &=&\frac {66\times 10^{3}\times 66\times 10^{3}}{11}\sin 30° \\[ 5pt ] &=&198\times 10^{6} \ \mathrm {[W]}　→　198 \ \mathrm {[MW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。